
Основы теории вероятностей (Евдокимович)
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ |
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ |
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ |
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА» |
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА» |
Кафедра «Прикладная математика» Кафедра «Прикладная математика»
В. Е. ЕВДОКИМОВИЧ В. Е. ЕВДОКИМОВИЧ
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ |
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ |
Учебно-методическое пособие для студентов |
Учебно-методическое пособие для студентов |
всех специальностей факультета УПП |
всех специальностей факультета УПП |
Одобрено методической комиссией факультета УПП
Гомель 2007 |
Гомель 2007 |
1
УДК 519.2(075.8) ББК 22.171
Е15
Рецензент – зав. кафедрой высшей математики д-р физ.-мат. наук В. Н. Семенчук (УО «ГГУ им. Ф.Скорины»).
Евдокимович, В. Е.
Е15 Основы теории вероятностей : учеб.-метод. пособие для всех специальностей факультета УПП / В. Е. Евдокимович ; М-во образования Респ. Беларусь, Белорус. гос. ун-т трансп. – Гомель : БелГУТ, 2007. – 122 с.
ISBN 978-985-468-347-8
Содержит основные разделы теории вероятностей, предусмотренные учебной программой по специальностям 1-44 01 01 «Организация перевозок и управление на автомобильном и городском транспорте», 1-44 01 03 «Организация перевозок и управление на ж.-д. транспорте», 1-44 01 04 «Организация перевозок и управление на речном транспорте» по дисциплине «Теория вероятностей и математическая статистика». Включает в себя теоретические сведения, предметные постановки и примеры решения задач, связанных с анализом вероятностных характеристик процессов управления перевозок на транспорте.
Предназначено для студентов всех специальностей факультета УПП. Может быть использовано при выполнении курсовых и дипломных проектов студентами, аспирантами и научными работниками, занимающимися вероятностными методами.
УДК 519.2(075.8) ББК 22.171
ISBN 978-985-468-347-8 |
© Евдокимович В. Е., 2007 |
|
© Оформление. УО «БелГУТ», 2007 |
2
ВВЕДЕНИЕ
Последние годы характеризуются интенсивным внедрением вероятностных методов в технологические, социологические и экономические науки в связи с развитием массовых процессов в производстве и экономике. Поэтому знание методов теории вероятностей необходимо инженерам при разработке математических моделей для решения практических задач.
Теория вероятностей изучает модели экспериментов со случайными исходами (случайных экспериментов). Всякий случайный эксперимент (испытание) состоит в осуществлении некоторого вполне определенного комплекса условий и наблюдении результата. Рассматриваются только такие эксперименты, которые можно повторить при неизменном комплексе условий произвольное число раз.
Предметом наблюдения в том или ином случайном опыте может быть некоторый процесс, физические явления или действующая система. Для реально воспроизводимого эксперимента понятие “наблюдаемый результат” означает, что существует принципиальная возможность зарегистрировать данный результат опыта с помощью того или иного прибора. Любой наблюдаемый результат интерпретируется как случайный исход опыта (случайное событие). Событие может произойти, а может не произойти в результате эксперимента.
При математической формализации модели случайного эксперимента основным пунктом является понятие множества (пространства) элементарных исходов (событий), связанного с данным экспериментом. Под этим понимают множество взаимоисключающих исходов, такое, что результатом эксперимента всегда является один и только один исход. Любое подмножество данного множества рассматривается как событие.
3
Результат эксперимента можно охарактеризовать количественно. Количественная характеристика эксперимента состоит в определении значений некоторых величин, которыми интересуются при данном эксперименте. В силу действия большого числа случайных факторов эти величины могут принимать различные значения в результате эксперимента. Поэтому такие величины называют случайными.
Теория вероятностей занимается изучением случайных событий и случайных величин.
В пособии содержатся основные сведения из теории вероятностей (определения, леммы, теоремы), рассматривается множество примеров, а также содержатся задания по РГР.
4
1 СЛУЧАЙНЫЕ СОБЫТИЯ
1.1Вероятностный эксперимент. Пространство элементарных событий
Любой эксперимент или наблюдение изучаемого физического явления заканчивается некоторым событием (исходом). Если результат эксперимента заранее однозначно непредсказуем, то данный эксперимент называется вероятностным и обозначается символом «Е».
Элементарным событием (элементарным исходом) ω называется любой мысленно возможный неразложимый результат вероятностного эксперимента Е.
Пространством элементарных событий Ω называется множество всех мыслимых взаимоисключающих результатов вероятностного эксперимента Е.
Случайным событием называется такое событие, о котором нельзя заведомо точно сказать, произойдёт оно или нет.
Случайные события обозначаются заглавными латинскими буквами (A, B, C, D, …). Случайное событие является некоторым подмножеством пространства элементарных событий ( A Ω ).
Пример 1
Е: бросается игральная кость.
Элементарные события: ω1 = {выпадение на игральной кости «1»}, ω2 = {выпадение на игральной кости «2»} и т. д. Пространство элементарных событий Ω = {выпадение на игральной кости числа от «1» до «6»} = { ω1 , ω2 , …, ω6 }. Тогда случайные события:
A = {выпадение чётного числа} = {ω2 , ω4 , ω6 };
B = {выпадение нечётного числа} = {ω1 , ω3 , ω5 }; C = {выпадение «5»} = { ω5 };
D = {невыпадение «3»} = {ω1 , ω2 , ω4 , ω5 , ω6 };
F = {выпадение числа от «3» до «5»} = { ω3 , ω4 , ω5 }; 5

G = {выпадение числа > 4} = { ω5 , ω6 };
I = {выпадение числа < 4} = {ω1 , ω2 , ω3 }.
В зависимости от размерности множества возможных элементарных событий, различают конечное, счётное и несчётное пространство элементарных событий Ω .
В примере 1 пространство элементарных событий Ω является конечным, поскольку включает лишь 6 элементарных событий. В эксперименте с исследованием числа поездов, прибывающих на станцию в течение суток, пространство элементарных событий Ω счётно, т. к. каждому элементарному событию эксперимента можно поставить в однозначное соответствие число натурального ряда. В эксперименте с исследованием времени обслуживания поезда на станции, пространство элементарных событий Ω несчётно, т. к. время обслуживания может принимать любые положительные значения.
Элементарные события, которые образуют случайное событие A, называются благоприятными событию A.
В примере 1 элементарные события ω2 , ω4 , ω6 являются благоприятными событию A, элементарные события ω1 , ω3 , ω5 – благо-
приятными событию B и т. д.
В частном случае множество элементарных исходов, благопрятных событию A, может совпадать с пространством элементарных событий Ω или быть пустым множеством Ø.
Достоверным событием называется событие, которое всегда происходит, т. е. совпадающее с пространством элементарных событий Ω .
Невозможным событием называется событие, которое никогда не произойдёт, т. е. совпадающее с пустым множеством.
В примере 1 достоверным событием является случайное событие K = {выпадение числа от «1» до «6»} = Ω , а невозможным событием является, например, случайное событие L = {выпадение числа «7»} = Ø.
1.2 Операции над событиями
Пусть имеется пространство элементарных событий Ω . Будем рассматривать в качестве случайных событий подмножества A, B, C, … этого пространства.
6
Суммой (объединением) событий A и B называется третье событие А+В (A B) , состоящее в осуществлении хотя бы одного из со-
бытий А или В. Благоприятными событию А В являются все элементарные события, благоприятные хотя бы одному из событий А или В.
Аналогично определяется сумма любого числа событий
А1 А2 А3 K .
Произведением (пересечением) событий А и В называется третье событие АВ(A ∩ B) , состоящее в одновременном осуществлении
событий А и В. Благоприятными событию А∩ В являются все элементарные события, благоприятные одновременно событию А и событию В.
Произведение любого числа событий А1 ∩ А2 ∩ А3 K состоит в одновременом осуществлении событий А1, А2 , А3 и т. д.
Разностью событий А и В называется третье событие А–В (А\В), состоящее в осуществлении события А без осуществления события В. Событие А\В состоит из элементарных событий благоприятных событию А, за исключением элементарных событий благоприятных событию В.
Противоположным событию А называется событие А , состоя-
щее в ненаступлении события А. Событию А благоприятны все возможные элементарные события пространства элементарных событий
Ω , кроме тех, которые благоприятны событию А ( А = Ω \ А ). События А и В называются несовместными, если они не могут
произойти одновременно, т. е. одновременное осуществление событий А и В есть событие невозможное ( А ∩ В = Ø).
События А1, А2 , А3, K , Аn образуют полную группу событий, если их сумма составляет пространство элементарных событий Ω ( А1 А2 А3 K Аn = Ω ), т. е. в результате эксперимента хотя бы одно из событий произойдёт.
Пример 2
Рассмотрим операции над событиями, используя условия из примера 1.
7
а) А В = {ω1, ω2 , ω3, ω4 , ω5, ω6} = Ω; А C = {ω2 , ω4, ω5, ω6};
CI = {ω1, ω2, ω3, ω5};
CD = {ω1, ω2 , ω4, ω5, ω6}; F G = {ω3, ω4 , ω5, ω6};
б) А∩ В = Ø;
В ∩ С = {ω5};
D ∩ F = {ω5, ω6};
G ∩ I = Ø;
C ∩ G = {ω5};
в) А \ В = Ø;
B \ C = {ω1, ω3};
D \ F = {ω1, ω2 , ω6};
G\ I = {ω5, ω6} = G;
G\ C = {ω6};
г) A = Ω \ A = {ω1, ω3, ω5} = B; B = Ω \ B = {ω2 , ω4 , ω6} = A;
C = Ω \ C = {ω1, ω2 , ω3, ω4 , ω6}; D = Ω \ D = {ω3};
F = Ω \ F = {ω1, ω2 , ω6};
д) События А и В образуют полную группу событий, т. к.
А В = Ω .
Пример 3
Е: в прямоугольник (рисунок 1) наудачу бросается точка. Элементарное событие данного эксперимента – некоторая точка
внутри прямоугольника. Пространство элементарных событий Ω (в данном случае – несчётное) – всё множество точек внутри прямоугольника. На множестве Ω определены два события: А={выбранная точка лежит внутри круга А} и В = { выбранная точка лежит внутри круга В}.
8
AB
Ω
Рисунок 1 – Диаграмма Венна-Эйлера
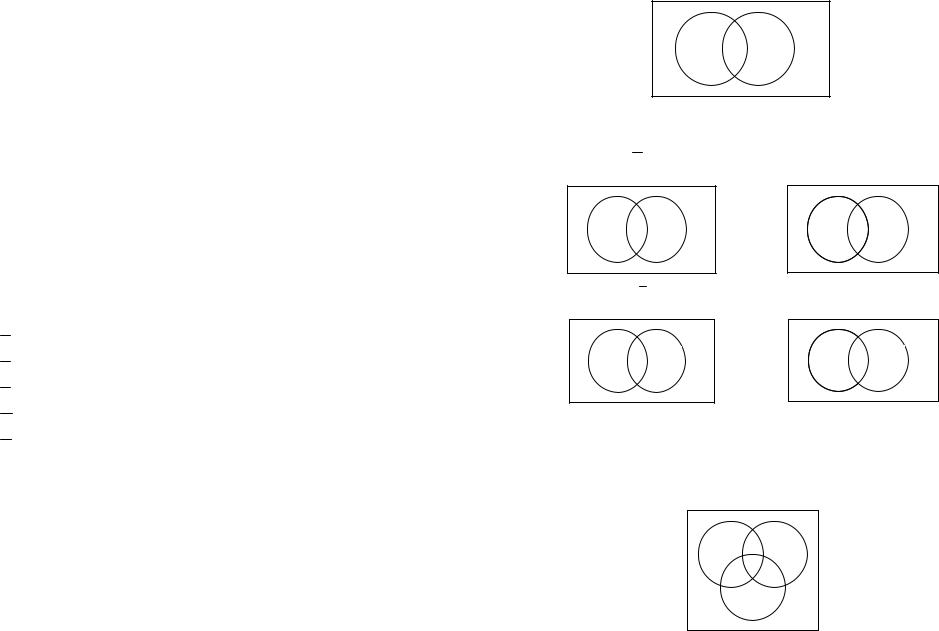
Изобразим области, попадание в которые соответствует осуществлению событий А , А В , А ∩ В , А \ В :
A |
B |
A |
B |
|
Ω |
|
Ω |
|
A |
|
A B |
A |
B |
A |
B |
|
Ω |
|
Ω |
|
A∩ B |
|
A \ B |
Пример 4
Е: в прямоугольник наудачу бросается точка.
A B
C
Ω
9
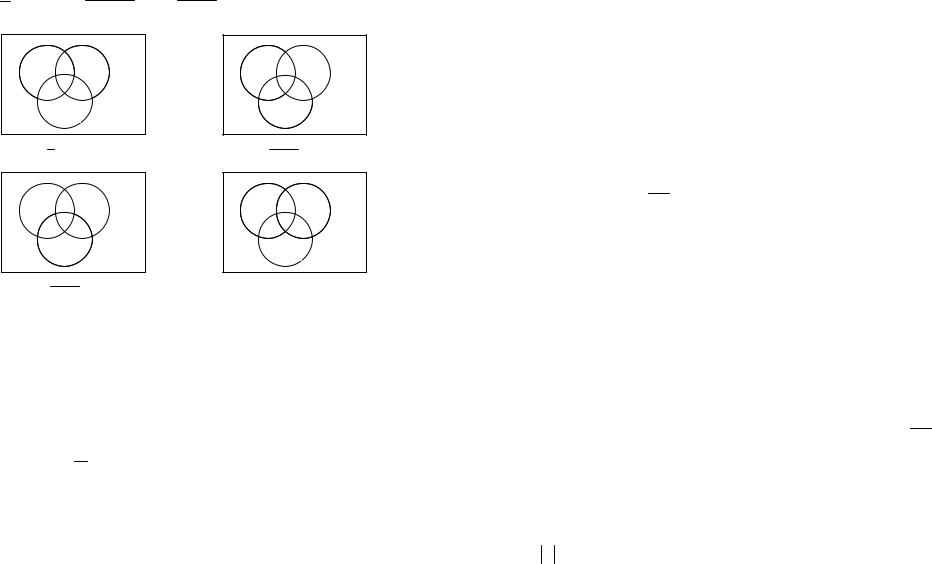
На множестве Ω определены три события: А = {выбранная точка лежит внутри круга А}, В = {выбранная точка лежит внутри круга В}, С = {выбранная точка лежит внутри круга С}. Изобразим области, попадание в которые соответствует осуществлению следующих со-
бытий А ∩ (В \ С), (A B) ∩ С , А∩ В \ С , А \ В С :
AB
СΩ
A∩ (B \ С)
AB
СΩ
A ∩ B \ C
AB
СΩ
(A B) ∩ C
AB
СΩ
A \ B C
1.3 Вероятности случайных событий
1.3.1 Относительная частота случайного события
Пусть было проведено n вероятностных экспериментов Е, при этом случайное событие А произошло m раз.
Число m называется частотой появления случайного события А,
а отношение P* = m – относительной частотой (частостью) слу- n
чайного события А.
Относительная частота наступления некоторого случайного события не является постоянной величиной, однако она обладает устойчивостью, стремлением к некоторому постоянному числу и колебания её тем меньше, чем больше проведено экспериментов.
10
1.3.2Понятие вероятности случайного события. Аксиомы Колмогорова
Вероятностью случайного события А называется числовая функция Р(А), определённая на пространстве элементарных событий Ω , характеризующая меру объективной возможности наступления события А и удовлетворяющая для каждого случайного события аксиомам Колмогорова А. Н.
Аксиома 1. P(A) ≥ 0, т. е. вероятность наступления произвольного случайного события – неотрицательная функция.
Аксиома 2. P(Ω) = 1, т. е. вероятность наступления достоверного события равна 1.
|
∞ |
|
∞ |
Аксиома 3. |
P U Ai = ∑P(Ai ) , Ai ∩ Aj = Ø, i ≠ j , т. е. веро- |
||
|
i=1 |
|
i=1 |
ятность наступления суммы счётного множества попарно несовместных событий Аi , i = 1,∞ равна сумме вероятностей этих событий.
1.4 Методы вычисления вероятностей
1.4.1 Классический метод вычисления вероятностей
Пусть пространство элементарных событий Ω некоторого вероятностного эксперимента Е конечно (ω1, ω2 , K , ωn ) и все элемен-
тарные события равновозможны, т. е. P(ω1) = P(ω2 ) = K = P(ωn ) . По классическому (лапласовскому) методу вероятность случайно-
го события А равна отношению числа элементарных событий NA , благоприятных событию А, к общему количеству элементарных со-
бытий N пространства элементарных событий Ω , т. е. P(A) = NA .
Учитывая, что А и Ω – множества (элементарных |
N |
||||||
событий), |
|||||||
можно записать: |
|
|
|
|
|
|
|
P(A) = |
|
|
A |
|
|
, |
(1) |
|
|
|
|
||||
|
|
Ω |
|
||||
|
|
|
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
где А – количество элементарных событий, благоприятных событию А;
11

Ω – общее количество элементарных событий пространства элемен-
тарных событий Ω .
Классический метод вычисления вероятностей имеет следующие
ограничения:
а) все элементарные события вероятностного эксперимента Е должны быть равновозможными, т. е. P(ωi ) = P(ωj ) , i, j ;
б) множество элементарных событий пространства Ω должно быть конечным, чтобы отношение А/ Ω не являлось неопределённостью ∞ /∞ .
Пример 5
Е: бросается игральная кость.
Найдём вероятности случайных событий из примера 1.
P(A) = 12 ; P(B) = 12 ; P(C) = 16 ; P(D) = 56 ; P(F) = 12 ; P(G) = 13 ; P(I) = 12 .
Пример 6
Е: разгрузка вагонов на сортировочной станции.
На сортировочную станцию прибывают вагоны из Минска, Гомеля и Бреста. Предполагая равновозможными все варианты очерёдности разгрузки этих трёх вагонов, найти вероятности следующих случайных событий:
А = {вагон из Гомеля будет разгружен первым};
B = {вагон из Бреста будет разгружен не ранее, чем вагон из Минска}.
Решение. Пространство элементарных событий Ω в данном эксперименте состоит из шести элементарных событий
{ω1, ω2 , ω3, ω4 , ω5, ω6}. Введём условные обозначения элементар-
ных событий по первым буквам названий городов Ω = {ГМБ, ГБМ, МГБ, МБГ, БГМ, БМГ}, где, например, элементарное событие МГБ соответствует такой последовательности разгрузки: из Минска – из Гомеля – из Бреста. Тогда
12
А = {ГМБ, ГБМ}, P(A) = 62 = 13 ,
B = {ГМБ, МГБ, МБГ}, P(B) = 36 = 12 .
1.4.2 Элементы комбинаторики
Комбинаторика – раздел математики, изучающий количество комбинаций, подчинённых некоторым условиям.
Лемма 1 (основная лемма комбинаторики)
Из m элементов первого множества {a1, a2 , K, am } и n элементов второго множества {b1, b2, K , bn} можно составить ровно mn различных упорядоченных пар (ai , bj ) , содержащих по одному элементу из каждого множества.
Пример 7
Рассмотрим две группы элементов: ♠ – пики, ♣ – трефы, ♥ – черви, ♦ – бубны и 6, 7, 8, 9, 10, валет, дама, король, туз. По лемме 1 число пар 4·9 = 36. Это чило равно числу карт в колоде, т. к. каждая карта определяется парой элементов (масть и значение).
Пример 8
На «горном» велосипеде 3 передние и 6 задних звездочек. Сколько скоростей у «горного» велосипеда?
Решение. Так как каждая скорость велосипеда – комбинация одной из 3 передних ( n1 = 3) и одной из 6 задних ( n2 = 6) звездочек, то
количество скоростей на велосипеде равно количеству комбинаций звездочек двух типов и определяется, в соответствии с леммой 1,
произведением n1n2 = 3 6 =18 скоростей.
Пример 9
Е: бросаются две игральные кости.
Определим элементарное событие как пару ω = (i, j) , где i –
число очков, выпавших на первой кости, j – число очков, выпавших на второй кости. Тогда i выбирается из группы 1, 2, 3, 4, 5, 6; j выби-
13

рается из этой же группы. По лемме 1 число всех элементарных событий (т. е. всевозможных пар (i,j)) 6 · 6 = 62 = 36.
Лемма 2 |
|
|
|
Из n1 элементов первого множества {a1, a2 , |
K , |
an1 }, n2 эле- |
|
ментов второго множества {b1, b2 , K, bn2} и т. д., nk |
элементов k- |
||
го множества {x1, x2 , K, xnk } можно |
составить |
ровно |
|
n1 n2 K nk различных упорядоченных комбинаций (ai , bj , |
K, xs ), |
||
содержащих по одному элементу из каждого множества. |
|
||
Пример 10
Е: бросаются три игральные кости.
Элементарное событие ω = (i, j, k) , где i – число очков, выпав-
ших на первой кости, j – на второй кости, k – на третьей кости. По лемме 2 число всех элементарных событий (т. е. всевозможных ком-
бинаций (i, j, k)) будет 6 · 6 · 6 = 63 = 216.
Пример 11
Из пункта А в пункт В проходит 10 дорог, из пункта В в пункт С – 5 дорог, из пункта С в пункт D – 6 дорог. При этом все дороги, ведущие из А в D, проходят сначала через В, а затем через С. По лемме 2 из пункта А в пункт D проходит 10 · 5 · 6 = 300 дорог.
Перестановками называются комбинации n различных элементов и отличающиеся только порядком их расположения. Количество воз-
можных перестановок n различных элементов обозначается Pn = n!
Упорядоченными выборками (размещениями) называются комбинации, составленные из n различных элементов по m элементов, различающиеся либо составом элементов, либо их порядком. Количество возможных размещений m элементов из n различных элементов
обозначается Аnm .
Неупорядоченными выборками (сочетаниями) называются комбинации, составленные из n различных элементов по m элементов, различающиеся только составом элементов. Количество возможных
сочетаний m элементов из n различных элементов обозначается Сnm . Упорядоченные и неупорядоченные выборки, элементы которых
14
могут повторяться, называются соответственно упорядоченными и неупорядоченными выборками с повторением. Количество возможных упорядоченных и неупорядоченных выборок m элементов из n различных элементов с повторением обозначается соответственно
A~nm и С~nm .
Таблица 1 - Числа выборок объёма m из множества {a1, a2 ,K, an }
Выборки |
Упорядоченные |
Неупорядоченные |
|||||||
(размещения) |
|
(сочетания) |
|||||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
С повторением |
~m |
= n |
m |
~m |
= C |
m |
|||
(с возвращением) |
A |
|
|
С |
n |
n+m−1 |
|||
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
Без повторения |
Аm = |
n! |
Сm = |
|
n! |
||||
|
|
|
|
|
|
||||
(без возвращения) |
n |
(n − m)! |
n |
|
(n − m)!m! |
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Пример 12
Сколькими способами можно расположить три шара, пронумерованных цифрами «1», «2», «3»?
Решение. Поскольку комбинации расположения трёх различных шаров отличаются лишь порядком расположения, то данные комбинации называются перестановками. Перечислим все возможные способы перестановками трёх шаров: «1-2-3», «1-3-2», «2-1-3», «2-3-1», «3-1-2», «3-2-1». Таким образом, количество всевозможных перестановок равно 6.
Пример 13
Перечислить все возможные способы выбора двух шаров из урны с тремя шарами, пронумерованными числами «1», «2», «3».
Таблица 2 - Способы выбора 2 шаров из урны с 3 пронумерованными шарами
Выборки |
Упорядоченые |
Неупорядоченные |
|
(размещения) |
(сочетания) |
||
|
|
(1,1) |
(1,2) |
(1,3) |
(1,1) |
(1,2) |
(1,3) |
С повторением |
(2,1) |
(2,2) |
(2,3) |
|
(2,2) |
(2,3) |
(с возвращением) |
|
|||||
(3,1) |
(3,2) |
(3,3) |
|
|
(3,3) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
(1,2) |
(1,3) |
|
(1,2) |
(1,3) |
Без повторения |
(2,1) |
|
(2,3) |
|
|
(2,3) |
(без возвращения) |
|
|
|
|||
(3,1) |
(3,2) |
|
|
|
|
|
|
|
|
|
|
15
Пример 14
На железнодорожной станции имеются 10 путей. Сколькими способами можно расставить на них три состава?
Решение. Поскольку комбинации расположения трёх различных составов на 10 путях отличаются лишь расположениями, то данные комбинации являются упорядоченными выборками без возвращения. Количество всевозможных размещений в этом случае равно
Аnm = А103 = 720 .
Пример 15
В вагон электрички, делающей 9 остановок, на первой остановке вошли два пассажира. Каждый из них, с одинаковой вероятностью, выходит на любой из остановок, начиная со второй. Найти вероятность того, что оба пассажира выйдут на одной остановке.
Решение. Пусть случайное событие А = {два пассажира выйдут на
одной остановке}. По классическому методу P(A) = NA , где
N
NA = 8 – число элементарных событий, благоприятных событию А, а
N= A~nm = nm = 82 = 64 – число всевозможных элементарных собы-
тий пространства Ω . Таким образом, P(A) = 648 = 18 = 0,125.
1.4.3 Геометрический метод вычисления вероятностей
Если пространство элементарных событий Ω вероятностного эксперимента Е является несчетным, то для вычисления вероятностей случайных событий может применяться геометрический метод.
Пусть пространство Ω эксперимента E содержит несчетное множество элементарных исходов ω (т. е. Ω = ∞ ) и их можно тракто-
вать как точки в евклидовом пространстве, а события эксперимента
E – как некоторые ограниченные области этого пространства. Тогда вероятность случайного события A может быть определена выражением
P(A) = |
µ(A) |
, |
(2) |
|
µ(Ω) |
||||
|
|
|
||
16 |
|
|
|
где µ(A) – геометрическая мера (длина, площадь, объём) области, соответствующая событию A; µ(Ω) – геометрическая мера области, соответствующая пространству элементарных событий Ω.
Пример 16
Простой состава в ожидании осмотра бригадой пункта технического осмотра (ПТО) в парке прибытия сортировочной станции равно возможен в интервале [0; 50 мин]. Простой в ожидании расформирования состава также равновозможен в интервале [0; 40 мин].
Найти вероятность того, что нерегламентированный простой состава в парке прибытия не привысит 20 минут.
Решение. Пространством элементарных событий Ω этого эксперимента является прямоугольник, изображённый на рисунке 5, т. е.
Ω = {ω = (x, y) | 0 ≤ x ≤ 50,0 ≤ y ≤ 40}.
y 40
20 А |
|
Ω |
|
||
0 |
|
|
|
|
|
|
20 |
50 |
x |
||
|
|
||||
Рисунок 2 – Геометрическая интерпретация вероятностного эксперимента
Событию A = {ω = (x, y) | x + y ≤ 20}={простой состава не пре-
высит 20 минут} соответствует заштрихованная на рисунке область. Следовательно,
P(A) = |
SA |
= |
0,5 20 20 |
= 0,1. |
|
SΩ |
40 50 |
||||
|
|
|
Пример 17
Два теплохода должны подойти к одному причалу. Моменты прихода обоих теплоходов независимы и равновозможны в течение суток. Определить вероятность того, что одному из теплоходов придётся ожидать на рейде, пока не освободится причал, если время стоянки теплоходов равно одному часу.
17

Решение. Пространством элементарных событий Ω этого эксперимента является прямоугольник, изображённый на рисунке 6, т. е.
Ω = {ω = (x, y) | 0 ≤ x ≤ 24, 0 ≤ y ≤ 24}. |
|
||
y |
|
|
|
24 |
|
23 |
|
|
|
|
|
|
|
23 |
|
1 |
A |
Ω |
|
|
|
||
0 |
1 |
24 |
x |
Рисунок 3 – Геометрическая интерпретация |
|||
|
|
вероятностного эксперимента |
|
Событию A = {ω = (x, y) || x − y |≤ 1}={одному из теплоходов
придётся ожидать на рейде} соответствует заштрихованная на рисунке область. Следовательно,
P(A) = |
SA |
= |
242 − 232 |
= |
47 |
≈ 0,082 . |
|
|
242 |
576 |
|||||
|
S |
Ω |
|
|
|
||
|
|
|
|
|
|
|
|
1.4.4Статистический и экспертный методы вычисления вероятностей
Кроме классического и геометрического существуют еще два способа определения вероятностей случайных событий: статистический и экспертный. Статистический способ заключается в оценке вероятности случайного события по результатам многократного воспроизведения вероятностного эксперимента E, например, по относительной частоте появления случайного события.
Метод экспертных оценок заключается в опросе мнения некоторого количества экспертов о значении вероятности случайного события. Анализируя полученные значения экспертных оценок, можно получить представление о реальном значении вероятности исследуемого случайного события.
Статистический и экспертный способы оценки вероятностей яв-
ляются универсальными, однако, предоставляемый с их помощью результат не является точным. Для увеличения достоверности и точности оценки вероятности требуется проведение большего количества повторных экспериментов и привлечение большего числа опытных экспертов.
1.5 Свойства вероятностей случайных событий
Вероятности случайных событий обладают следующими важными свойствами:
Свойство 1. P(Ø) = 0, т. е. вероятность невозможного события равна 0.
Свойство 2. Если в пространстве Ω , содержащем конечное или счётное множество возможных элементарных событий
ω1, ω2, K, ωi , K (Ω = {ω1, ω2 , K, ωi , K}), заданы вероятности элементарных событий P(ω1) = p1, P(ω2 ) = p2 , K, P(ωi ) = pi , K, то вероятность произвольного события A = {ωj , ωk ,K, ωl} равна сумме вероятностей элементарных событий, благоприятных событию
А, т. е. P(A) = ∑P(ωi ).
ωi A
Говорят, что событие А влечёт событие В (A B) , если все элементарные события ωi , благоприятные событию А, благоприятны событию В (рисунок 4).
Свойство 3. Если A B , то P(B \ A) = P(B) − P(A).
B
A
Ω
Рисунок 4 – Пример события А, которое влечёт событие В
18 |
19 |
