
- •Введение
- •1 Анализ существующих амортизирующих устройств
- •1.1 Расположение элементов подвески
- •1.2 Элемент упругий пневматический
- •1.3 Регулятор положения кузова
- •1.4 Амортизатор гидравлический
- •2 Подробное описание и принцип действия предлагаемого
- •2.1 Расчет основных размеров предлагаемого устройства
- •2.2 Анализ эффективности предлагаемого устройства
- •3 Организация ремонта и проектирование агрегатного участка
- •3.1 Расчет фондов рабочего времени
- •3.2 Расчет программы ремонта
- •3.3 Расчет основных параметров производственного процесса
- •3.4 Расчет трудоемкости программы ремонта
- •3.5 Расчет численности рабочих
- •4 Технико-экономические показатели участка
- •4. 1 Фонд оплаты труда
- •4.2 Отчисления на социальную защиту и в пенсионный фонд
- •4.3 Амортизация основных средств
- •4.4 Расход электроэнергии за смену
- •4.5 Тепловая энергия
- •4.6 Материалы для ремонта
- •4.7 Накладные общехозяйственные расходы ( в том числе прочие прямые расходы )
- •4.8 Экономическая эффективность внедрения разработанного технологического оборудования
- •На основе эмпирических данных было выяснено, что изношенные амортизаторы удлиняют тормозной путь на 2-3 метра (при торможении со скорости 60 км/час).[4]
- •На поворотах машина становится трудно управляемой – задние шины теряют сцепление с покрытием при прохождении поворотов из-за значительного возрастания силы поперечного ускорения.[5]
- •Увеличении эффективности амортизатора на каждые 5%, приводит к увеличению срока службы узлов ходовой части, шин и трансмиссии 2-3%.[6]
- •5 Разработка графика ремонта продукции участка
- •5.1 Определение трудоемкости ремонта заднего моста
- •5.2 Предварительный расчет численности при ремонте заднего моста
- •5.3 Разработка графика ремонта заднего моста
- •5.4 Разработка графика загрузки рабочих
- •5.5 Расчет оборотного задела сборочной единицы
- •5.6 Подбор оборудования агрегатного участка
- •5.7 Определение площади и размеров агрегатного участка
- •5.8 Определение числа и грузоподъемности подъемно-транспортных средств
- •6 Расчет потерь мощности и электроэнергии в
- •7 Охрана труда и окружающей среды
- •7.1 Разработка мероприятий по охране труда
- •Перечень графических работ
- •Технологическая документация
2.1 Расчет основных размеров предлагаемого устройства
Проектирование
амортизатора начинается с выбора
основных размеров, определяющих его
габариты: диаметр рабочего цилиндра
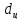 и ход поршня
и ход поршня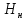 .
За основу принимаем амортизатор
находящийся сейчас в эксплуатации:50.2905006 (рисунок
12).
.
За основу принимаем амортизатор
находящийся сейчас в эксплуатации:50.2905006 (рисунок
12).

Рисунок 12 – Амортизатор 50.2905006
Тип- гидравлический, двух трубный, телескопический, двухстороннего действия
Длина амортизатора в сжатом состоянии – 345мм
Ход поршня-220 мм
Диаметр поршня 50мм
Диаметр штока-20 мм
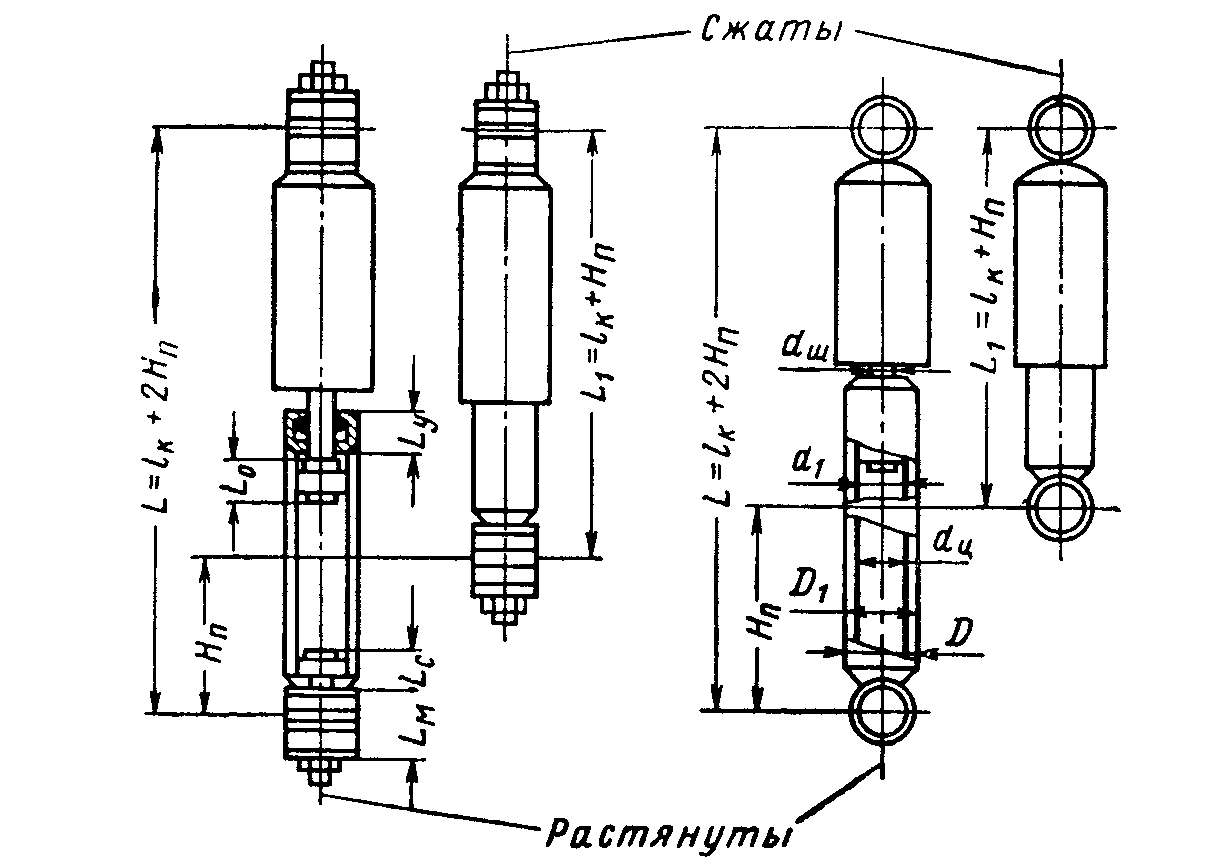


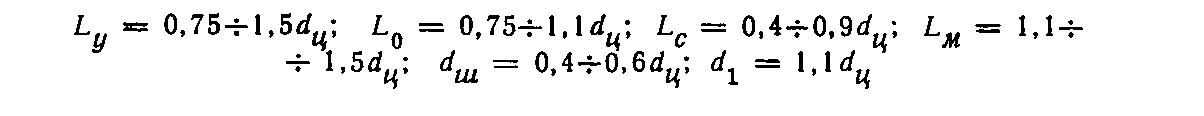
Рисунок 13 – Основные конструктивные размеры телескопических амортизаторов
С
диаметром штока и рабочего цилиндра
тесно связаны и размеры резервуара,
который должен вмешать определенный
оббьем жидкости и воздуха для осуществления
процесса рекуперации. При этом оббьем
воздуха должен быть примерно в 3 раза
больше объема штока (из расчета его
полного хода), что бы не создавались
излишне высокие давлении при работе.
Это соотношение выражается следующим
образом: 
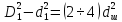 ;
;
Учитывая приведенные на рисунке 13 соотношения, найдем непосредственную связь
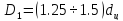
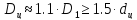
Тогда
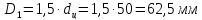
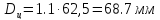
Основной рабочей площадью вытеснителя является площадь поршня в штоковой камере( на отдаче):
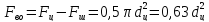
На сжатии
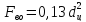
Тогда
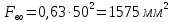

Выбираем из таблицы 2 по приведенным размерам усилия сопротивления
Таблица
2 – Таблица основных размеров и усилий
сопротивлений
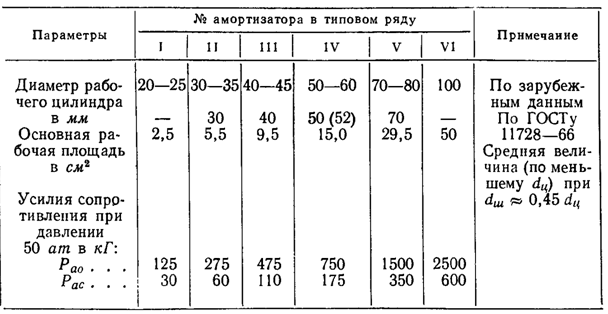

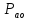 =750
кг,
=750
кг,
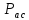 =175
кг
=175
кг
Так как тепловой режим работы амортизатора зависит от размеров его наружной поверхности, то на практике выбор тех или иных усилий сопротивлений ограничен не только диаметром рабочего цилиндра и резервуара, но и длиной
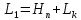 ,
,
Где
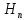 -ход
поршня,
-ход
поршня,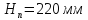 ;
;
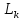 -конструктивная
длинна,
-конструктивная
длинна,
 .
.
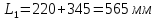
Площади теплоотдающей поверхности амортизаторов определяются с достаточной точностью, как у цилиндра без торцов:
![]()
Тогда
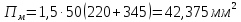
Ориентировочные
веса колеблющейся массы для типовых
амортизаторов, допускаемый вес
подрессоренной массы, вес транспортного
средства смотрим в таблице 3.
Таблица 3 – Ориентировочные веса колеблющейся массы для типовых
амортизаторов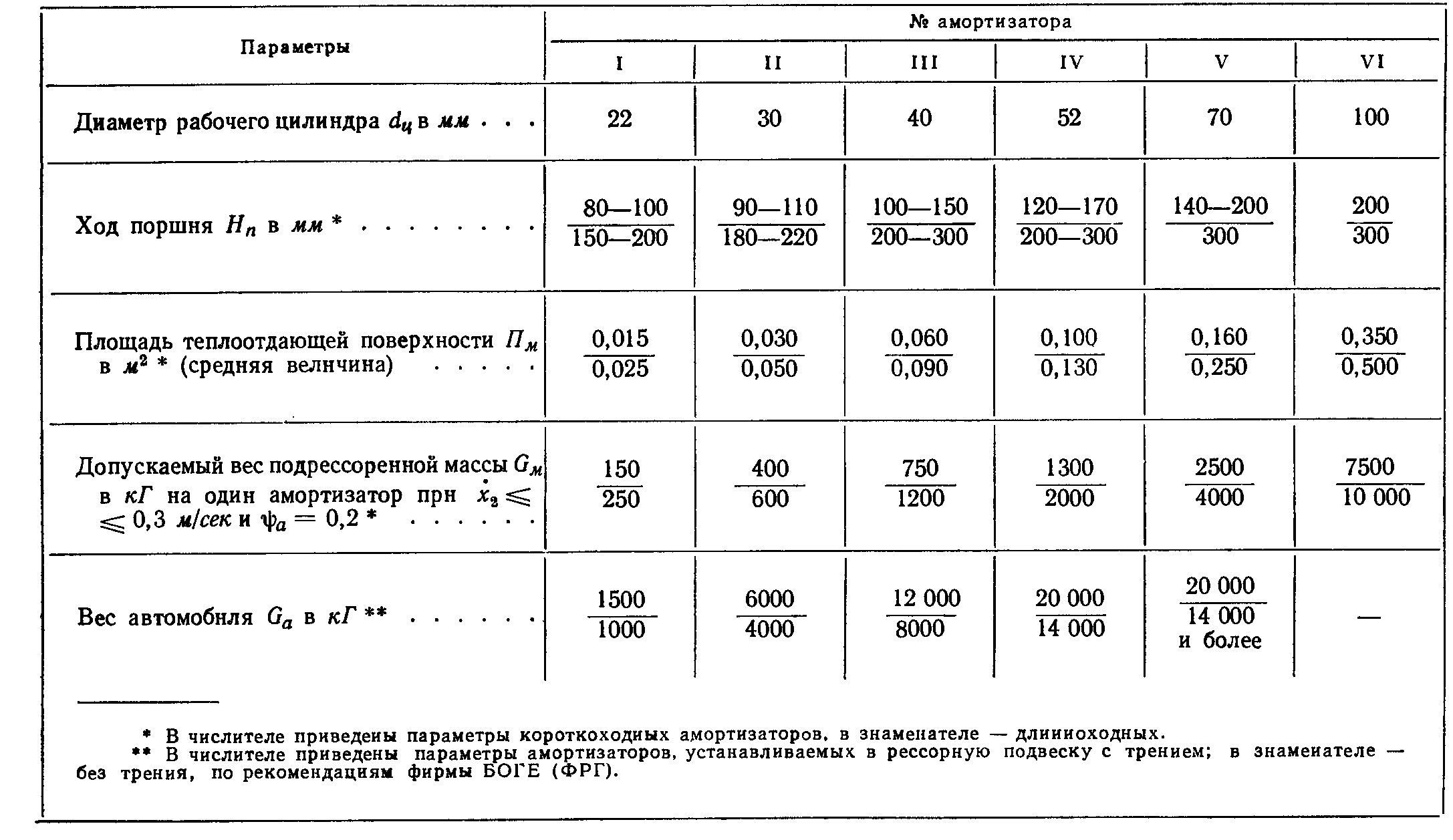
Выбираем
длинноходный амортизатор с ходом поршня
220 мм, площадью теплоотдающей поверхности
0,130
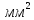 ,
допустимым весом неподрессоренной
массой на один амортизатор 2000 кГ, и весом
транспортного средства 14000 кг.
,
допустимым весом неподрессоренной
массой на один амортизатор 2000 кГ, и весом
транспортного средства 14000 кг.
2.2 Анализ эффективности предлагаемого устройства
Теоретические сведения, подтверждающие возможность осуществления изобретения с получением вышеуказанного технического результата, заключаются в следующем (Ю.Н.Санкин, С.Л.Пирожков. Управление полем виброперемещений упругих систем с распределенными параметрами, стр.71-79 // Механика и процессы управления: Сборник научных трудов / Ульяновский гос. техн. ун-т. Ульяновск, 2000. 84 с):
Рассмотрим нестационарные колебания системы с распределенными параметрами без наличия регулятора уровня вибраций. Эти колебания в линейном приближении описываются следующей системой дифференциальных уравнений:
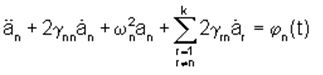
где an=an(t) - коэффициент разложения поля перемещений u в ряд по формам собственных колебаний:
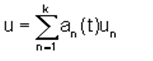
где
un -
форма колебаний; k - число существенно
проявляющих себя форм колебаний; -
интегральный коэффициент рассеяния
энергии;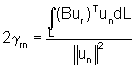
![]()
В- оператор рассеяния энергии; - норма со ответствующей формы колебаний; R - масса единицы длины, площади, объема; L - область, занимаемая упругим телом.

где f - возмущающие силы.
Пусть к рассматриваемой системе присоединены s сосредоточенных масс m; при помощи упругих элементов сi. Тогда получим следующую систему уравнений:
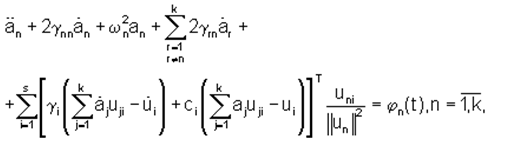
![]()
Здесь uji - вектор значений j-й формы колебаний в i-й точке упругой системы; γi - матрица рассеяния энергии в i-м упругом элементе; сi - матрица жесткостей i-го упругого элемента.
Чтобы выяснить принципиальную сторону вопроса, рассмотрим балку, несущую s упругоприсоединенных масс без учета рассеяния энергии. Положим, что все массы и соответствующие упругие элементы одинаковы: mi,=m, сi=с. Тогда система упроститься и перепишется в виде:
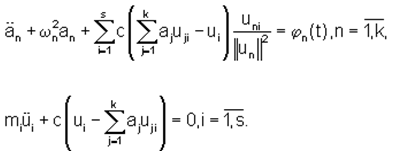

Далее пусть на систему действует гармоническая возмущающая сила f=f0sinωt, где f0 - амплитуда возмущающей силы; ω - ее частота. Тогда ϕn(t)=ϕn0sinωt
где
причем L здесь уже длина
балки.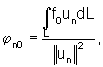
Ограничимся частным решением системы, то есть чисто вынужденной составляющей, полагая
![]()
где аn0, ui0 - соответствующие амплитуды вынужденных колебаний.
Подставляя в систему получаем:
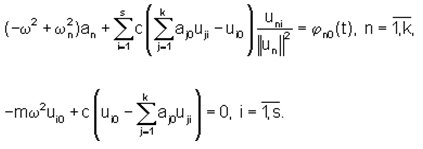

Нетрудно видеть, что при все aj0 обращаются в нуль, то есть имеет место гашение колебаний. При некотором отклонении частоты гашения ωг от частоты возбуждения и, если учитывать рассеяние энергии, амплитуда вибраций в точках крепления регуляторов будет отличаться от нуля. При этом амплитуда поддается управлению, если изменять массу m.
Данное устройство было проверено с помощью численного эксперимента. В упругую модель были заложены следующие исходные данные:
H1=Н2=100800 Н/м,
γ1=0,01; m1=6800 кг;
ρ1=0,58 м2;
a1=1,32 м; a2=1,08 м;
r=10;
m=3;
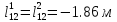 ;
;
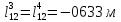 ;
;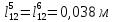 ;
;
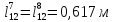 ;
;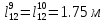 ;
;
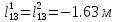 ;
; ;
;
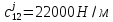 ;
;
;
;
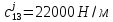 ;
;
γ2=0,01;
m2=1600кг;
ρ2=1,068м2;
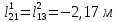 ;
;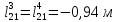 ;
;
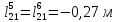 ;
;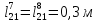 ;
;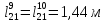 ; m3=250кг;ρ3=0,45м2;
; m3=250кг;ρ3=0,45м2;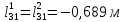 ;
;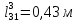 .
.
Где
H1,
H2 -
боковые жесткости шин передней и задней
оси; m1,
ρ1,
m2,
ρ2,
m3,
ρ3 -
массы и радиусы инерции рамы, кузова и
двигателя соответственно; γ1 -
коэффициент рассеяние энергии в шине;
γ2-
в подушках крепления кузова к раме; γ3 -
в подушках крепления двигателя к раме;
a1,
a2 -
расстояние от положения центра тяжести
до передней и задней осей; r - число
подушек крепления кузова к раме; m - число
подушек крепления двигателя к раме; ![]() -
расстояние от i-й подушки крепления
кузова до центра масс рамы;
-
расстояние от i-й подушки крепления
кузова до центра масс рамы;![]() -
жесткость в поперечном направлении i-й
подушки крепления кузова к раме;
-
жесткость в поперечном направлении i-й
подушки крепления кузова к раме;![]() -
расстояние от i-й подушки крепления
кузова до центра масс кузова;
-
расстояние от i-й подушки крепления
кузова до центра масс кузова;![]() -
расстояние от i-й подушки крепления
двигателя до центра масс рамы;
-
расстояние от i-й подушки крепления
двигателя до центра масс рамы;![]() -
жесткость в поперечном направлении i-й
подушки крепления двигателя к раме;
-
жесткость в поперечном направлении i-й
подушки крепления двигателя к раме;![]() -
расстояние от i-й подушки крепления
двигателя до центра масс двигателя;
-
расстояние от i-й подушки крепления
двигателя до центра масс двигателя;
Собственная
частота колебаний в поперечном направлении
была найдена и равна 20,9 с-1.
На рисунке 3 показана АЧХ и ее часть для
графического определения частоты
собственных колебаний. Для пружин с
жесткостью 2с=4400 Н/м требуемая масса
электромагнитной жидкости равна 10 кг.
Размер АФЧХ уменьшится примерно на 15%,
при этом значительно снижается амплитуда
колебаний автомобиля - на рисунок 4
показаны линейные АФЧХ двигателя ![]() и
АФЧХ двигателя с предлагаемым гасителем
и
АФЧХ двигателя с предлагаемым гасителем![]() Для вышеприведенных параметров упругой
системы автомобиля были построены АФЧХ
линейного, углового перемещения центра
масс, а также перекрестная АФЧХ: W11(iω),
W22(iω)
и W12(iω)
соответственно. По построенным АФЧХ
фиксируют характерные частоты -
экстремальные точки АФЧХ, соответствующие
минимальному значению мнимой составляющей
ωn и
максимальному значению вещественной
составляющей ωn
max.
По зафиксированным значениям ωn и
ωn
max определяют
постоянные времени:
Для вышеприведенных параметров упругой
системы автомобиля были построены АФЧХ
линейного, углового перемещения центра
масс, а также перекрестная АФЧХ: W11(iω),
W22(iω)
и W12(iω)
соответственно. По построенным АФЧХ
фиксируют характерные частоты -
экстремальные точки АФЧХ, соответствующие
минимальному значению мнимой составляющей
ωn и
максимальному значению вещественной
составляющей ωn
max.
По зафиксированным значениям ωn и
ωn
max определяют
постоянные времени:
![]()
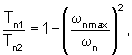
где Тn2, Tn1 - соответственно инерционная постоянная времени и постоянная времени демпфирования n-го колебательного звена. Смотри: Ю.Н.Санкин. Динамика несущих систем металлорежущих станков. - М.: Машиностроение, 1986. - 96 с.
В
работе: Динамические характеристики
вязкоупругих систем с распределенными
параметрами. Санкин Ю.Н. Издательство
Саратовского университета, 1977 г., дано
теоретическое представление передаточной
функции, являющейся математической
моделью эквивалентной упругой системы:
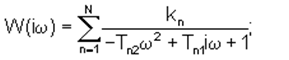

где -
соответствующие матрицы
коэффициентов усиления n-го колебательного
звена обозначая N-число
существенно проявляющихся витков АФЧХ.
Составим матрицу передаточных функций в виде:
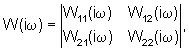
Матрица передаточных функций характеризует динамику бокового перемещения точки, принятой за полюс, и динамику угловых перемещений вокруг этого полюса, и представляет математическую модель упругой системы автомобиля в боковом движении.
Дополняя матрицу передаточных функций уравнениями неголономной связи шин с дорожным покрытием:
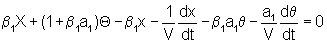
![]()
где β1, β2 - коэффициент деформации шин передней и задней оси; Х - поперечная координата центра тяжести автомобиля; х - поперечная координата прямоугольника, вершины которого - точки соприкосновения колес с дорожным покрытием; Θ - угол, определяющий направление автомобиля; θ - угол, определяющий направление прямоугольника вершины которого - точки соприкосновения колес с дорожным покрытием; a1, а2 - расстояния от передней и задней оси до положения центра тяжести; V - скорость движения автомобиля.
Передаточная матрица, соответствующая уравнениям неголономной связи
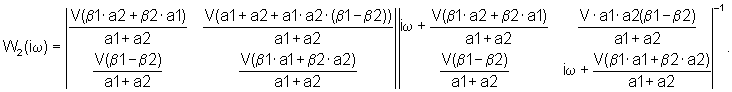
Общая передаточная матрица Н системы является произведением W(iω) и W2(iω): Н=W(ω)·W2(iω).
Рассмотрим динамическую устойчивость системы в линейной постановке (Ю.Н.Санкин. Динамика несущих систем металлорежущих станков. - М.: Машиностроение, 1986. - 96 с.). При неустойчивости определитель матрицы Н-I, где I - единичная матрица, должен равняется нулю. Соответственно ни одно собственное значение матрицы Н не должно равняться 1. Характеристическое уравнение для рассматриваемого случая:
![]()

Раскрывая определитель, получим квадратное уравнение:
λ2-(а11+а22)λ+(а11·а22-а21·а12)=0
Строя АФЧХ λ1 и λ2 согласно вышеуказанному уравнению, определяем, при какой скорости АФЧХ соответствующего λ пересекает вещественную ось при значении, равном 1.
Анализ показал, что при применении предлагаемого гасителя повышается курсовая устойчивость (увеличение критической скорости на 33,5% - до 68,4 км/ч). На рисунке 5 показаны годографы при скорости автомобиля V=68,4 км/ч: при скорости автомобиля V=68,4 км/ч: на а - годограф для автомобиля с предлагаемым гасителем, на b - без гасителя.
