1.2 Критерии сходимости при решении уравнений

• Абсолютная погрешность - абсолютное изменение  приближения на соседних шагах итерации

• Относительная погрешность - относительное изменение  приближения на соседних шагах итерации

• Близость к нулю вычисленного значения левой части уравнения (иногда  это значение называют невязкой уравнения, так как для корня невязка равна нулю)

1.3 Метод простой итерации

Это простейший из предложенных методов нахождения корней. В качестве итерационной формулы используется  выражение независимой переменной из исходного уравнения. Исходное уравнение путем арифметических преобразований приводится к виду, который может использоваться в качестве итерационной формулы. Данное преобразование, как правило, не однозначно и совершенно отдельной задачей является оценка применимости и эффективности того или иного способа преобразования.

Задавшись начальным приближением к корню (например, из анализа графика функции или априорных соображений физически реальной модели)  можно найти решение по итерационной схеме: (рисунок 2).

Рисунок 2. Точка - решение уравнения. Построение точкиx₁ по точке x₀

Например, уравнениеможно преобразовать, например, такили, илии т.д.

Например, итерационная схема при начальном приближении: x₀=1, итерационная последовательность: (рисунок 3.)

Рисунок 3. Последовательность итераций при поиске корня уравнения на отрезке[1, 2]; e=10^-8

Сходимостьметода простой итерации является локальной и резко зависит от выбора итерационной формулы, что является его недостатком. В случае сходимости скорость схождения не выше первой степени.

Пример решения уравнения методом простой итерации

Найти решение заданного уравнения методом простой итерации с точностью до 10^-8.

Пример создания расчетной схемы на основе метода простой итерации на примере уравнения: на отрезке [1, 2]

Итерационная схема метода: для данного уравнения: x₀= 1

a)	b)

Рисунок 1. Последовательность итераций метода простой итерации при поиске корня уравнения на отрезке [1, 2]

a) схема расчета (зависимые ячейки); b) режим отображения формул;

1.4 Метод секущих (метод хорд)

В данном методе процесс итераций состоит в том, что в качестве приближений к корню уравнения f(x)=0 принимаются значениях₁, х₂, ..., х_n точек пересечения хорды АВ с осью абсцисс (Рисунок 3). Сначала запишем уравнение хорды AB:

.

Для точки пересечения хорды AB с осью абсцисс (х = х₁, y = 0) получим уравнение:

Пусть для определенности f''(x) > 0 приа ≤ x ≤ b(случайf''(x) < 0 преобразуется, если записать уравнение в виде -f(x)= 0). Тогда криваяу = f(x)будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ. Возможны два случая:

1) f(а)> 0 (Рисунок 4, а)

2) f(a)< 0 (Рисунок 4, б).

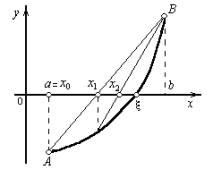
a) b)

Рисунок 4. Последовательное построение приближений методом хорд.

 

В первом случае конец анеподвижен, и последовательные приближения:

x₀ = b; i = 0,1,2,…

образуют ограниченную монотонно убывающую последовательность, причем .

Во втором случае неподвижен конец b, а последовательные приближения:

x₀ = а;

образуют ограниченную монотонно возрастающую последовательность, причем

Таким образом, если, тоx₀=b, c=a, иначеx₀=a, c=b и итерационная формула имеет вид:

Обобщая эти результаты, заключаем:

• неподвижен тот конец, для которого знак функции f(х)совпадает со знаком ее второй производнойf''(х);

• последовательные приближения x_nлежат по ту сторону корняx* , где функцияf(х)имеет знак, противоположный знаку ее второй производнойf''(х).

• Итерационный процесс продолжается до тех пор, пока не будет обнаружено, что , где- заданная предельная абсолютная погрешность.

Приведем расчетную схему для уравнения (рисунок 5).

Рисунок 5. Последовательность итераций при поиске корня уравнения на отрезке[1, 2]; e=10^-6