8. Применение теоремы Гаусса к расчету электростатического поля равномерно заряженной сферы и объемно заряженного шара.

П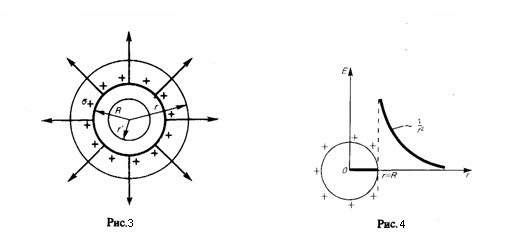оле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +σ. Т.к. заряд распределен равномернопо поверхности то поле, которое создавается им, обладает сферической симметрией. Значит линии напряженности направлены радиально (рис. 3). Проведем мысленно сферу радиуса r, которая имеет общий центр с заряженной сферой. Если r>R,ro внутрь поверхности попадает весь заряд Q, который создает рассматриваемое поле, и, по теореме Гаусса, 4πr²E = Q/ε₀ , откуда   (3) 

При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости Е от r приведен на рис. 4. Если r'<R, то замкнутая поверхность не содержит внутри себя зарядов, значит внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E=0). 

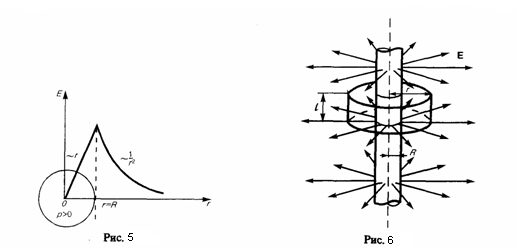 Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью ρ (ρ = dQ/dV – заряд, который приходится на единицу объема). Учитывая соображения симметрии, аналогичные п.3, можно доказать, что для напряженности поля вне шара получится тот же результат, что и в случае (3). Внутри же шара напряженность поля будет иная. Сфера радиуса r'<R охватывает заряд Q'=(4/3)πr'³ρ . Поэтому, используя теорему Гаусса, 4πr'²E=Q'/ε₀=(4/3)πr'³ρ/ε₀ . Т.к. ρ=Q/(4/3πR³)) получаем  (4) 

Значит, напряженность поля вне равномерно заряженного шара описывается формулой (3), а внутри его изменяется линейно с расстоянием r' согласно зависимости (4). График зависимости Е от r для рассмотренного случая показан на рис. 5. 

9. Работа сил электрического поля при перемещении заряда. Теорема о циркуляции напряженности электрического поля.

Элементарная работа, совершаемая силой F при перемещении точечного электрического заряда  из одной точки электростатического поля в другую на отрезке пути  , по определению равна

где  - угол между вектором силы F и направлением движения . Если работа совершается внешними силами, то dA0. Интегрируя последнее выражение, получим, что работа против сил поля при перемещении пробного заряда  из точки “а” в точку “b” будет равна

где  - кулоновская сила, действующая на пробный заряд  в каждой точке поля с напряженностью Е. Тогда работа

Пусть заряд  перемещается в поле заряда q из точки “а”, удалённой от q на расстоянии  в точку “b”, удаленную от q на расстоянии  (рис 1.12).

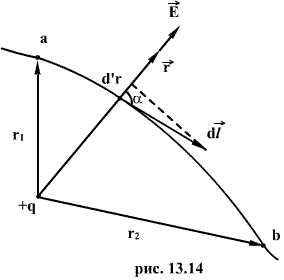
Как видно из рисунка  тогда получим

Как было сказано выше, работа сил электростатического поля, совершаемая против внешних сил, равна по величине и противоположна по знаку работе внешних сил, следовательно

Теорема о циркуляции электрического поля.

Напряженность и потенциал – это две характеристики одного и того же объекта – электрического поля, поэтому между ними должна существовать функциональная связь. Действительно, работа сил поля по перемещению заряда q из одной точки пространства в другую может быть представлена двояким образом:

Откуда следует, что

 

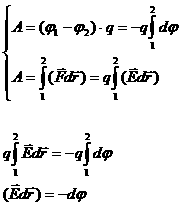
Или

Это и есть искомая связь между напряженностью и потенциалом электрического поля в дифференциальномвиде.

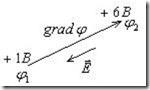
 - вектор, направленный из точки с меньшим потенциалом в точку с большим потенциалом (рис.2.11).

, .

Рис.2.11. Векторыи gradφ. .

Из свойства потенциальности электростатического поля следует, что работа сил поля по замкнутому контуру (φ₁= φ₂) равна нулю:

,

поэтому можем написать

Последнее равенство отражает суть второй основной теоремы электростатики – теоремы о циркуляции электрического поля, согласно которой циркуляция поля вдоль произвольного замкнутого контура равна нулю. Эта теорема является прямым следствием потенциальности электростатического поля.