23. Работа и мощность постоянного электрического тока. Кпд источника тока.

Работа А электрического тока на участке цепи с электрическим сопротивлением R за время D t равна:

A = I · U · ? t = I^{2 ·} R · ? t

Мощность P электрического тока равна отношению работы А тока ко времени D t, за которое эта работа совершена:

P = A / ? t = I · U = I² R = U² / R.

Работа А электрического тока равна количеству теплоты Q, выделяемому проводником (если не совершается механическая работа и не происходят химические реакции):

Q = I^{2 ·} R · ? t

Этот закон был экспериментально установлен английским ученым Джеймсом Джоулем (1818-1889) и русским ученым Эмилием Ленцем (1804-1865) и поэтому носит название закона Джоуля - Ленца.

   Рассмотрим элементарную электрическую цепь, содержащую источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R (рис. 7.5).

      КПД всегда определяем как отношение полезной работы к затраченной:

(7.8.1)

      Полезная работа – мощность, выделяемая на внешнем сопротивлении Rв единицу времени. По закону Ома имеем: а тогда

.

24. Вывод закона Ома из классической теории электропроводимости металлов.

Друде считал, что сразу после очередного соударения электрона с ионом кристаллической решетки скорость упорядоченного движения электрона равна нулю. Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное

и к концу пробега скорость упорядоченного движения достигнет значения

(18.2)

где t - среднее время между двумя последовательными соударениями электрона с ионами решетки. Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение средней скорости  . В этом приближении  , где  - среднее значение длины свободного пробега,  - скорость теплового движения электронов. Подставим это значение t в формулу (18.2)

Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального

Подставив это выражение в

получим

Плотность тока оказалась пропорциональной напряженности поля. Следовательно, мы получили закон Ома. Согласно  коэффициент пропорциональности между j и Е представляет собой проводимость

(18.3)

Если бы электроны не сталкивались с ионами решетки, длина свободного пробега, а, следовательно, и проводимость были бы бесконечно велики. Таким образом, электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами.

25. Вывод закона Джоуля-Ленца из классической теории электропроводности металлов. Затруднения этой теории.

К концу свободного пробега электрон приобретает скорость  , и, следовательно, дополнительную кинетическую энергию, средняя величина которой

Столкнувшись с ионом, электрон по предположению полностью теряет приобретенную им за время пробега скорость, и передает энергию кристаллической решетке. Эта энергия идет на увеличение внутренней энергии металла, проявляющееся в его нагревании. Каждый электрон претерпевает за секунду в среднем 1/t соударений, сообщая всякий раз решетке энергию  . Следовательно, в единице объема за единицу времени должно выделяться тепло

где n - число электронов проводимости в единице объема. Величина  есть не что иное, как удельная мощность тока. Множитель при  совпадает со значением  (18.3) для закона Ома. Таким образом. Мы пришли к выражению закона Джоуля-Ленца в дифференциальной форме.

Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемко­сти электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость ди­электриков, у которых нет свободных элек­тронов. Согласно закону Дюлонга и Пти (см. §73), теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоем­кость одноатомного электронного газа равна ³/₂R. Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т. е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электрон­ной теорией.

Указанные расхождения теории с опы­том можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а зако­нам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой. По­этому объяснить затруднения элементар­ной классической теории электропровод­ности металлов можно лишь квантовой тео­рией, которая будет рассмотрена в даль­нейшем. Надо, однако, отметить, что клас­сическая электронная теория не утратила своего значения и до настоящего времени, так как во многих случаях (например, при малой концентрации электронов проводи­мости и высокой температуре) она дает правильные качественные результаты и является по сравнению с квантовой тео­рией простой и наглядной.

25. Несамостоятельный и самостоятельный газовые разряды.

Н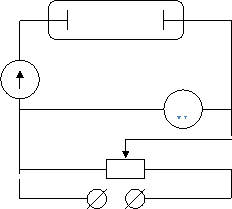есамостоятельный газовый разряд. Процесс прохождения электрического тока через газ называется газовым разрядом. Если электропроводность газа создается внешними ионизаторами, то электрический ток, возникающий в нем, называется несамостоятельным газовым разрядом. С прекращением действия внешних ионизаторов несамостоятельный разряд прекращается. Несамостоятельный газовый разряд не сопровождается свечением газа.  Ниже изображен график зависимости силы тока от напряжения при несамостоятельном разряде в газе. Для построения графика использовалась стеклянная трубка с двумя впаянными в стекло металлическими электродами. Цепь собрана как показано на рисунке

Самостоятельный газовый разряд.

Электрический разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом. Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Основным источником их возникновения является ударная ионизация молекул газа.

Если после достижения насыщения продолжать увеличивать разность потенциалов между электродами, то сила тока при достаточно большом напряжении станет резко возрастать (график 2).

Это означает, что в газе появляются дополнительные ионы, которые образуются за счет действия ионизатора. Сила тока может возрасти в сотни и тысячи раз, а число заряженных частиц, возникающих в процессе разряда, может стать таким большим, что внешний ионизатор будет уже не нужен для поддержания разряда. Поэтому ионизатор теперь можно убрать.