Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный аграрный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика. Часть 1

.pdf

Скачиваний:

Добавлен:

22.02.2016

Размер:

1.03 Mб

Скачать

☆

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

КОНТРОЛЬНЫЙ ТЕСТ ПО МОДУЛЮ №1

10. Определитель		1	2	равен:
		− 4	3
а) – 11;	б) 12;			в) – 4;	г) 11.

20. Если т = (3, 5, 6), то проекция этого вектора на ось Oz равна

а) 3;

б) 5;

в) 6;

г) 14.

равна

30. Длина вектора a

= 2i

− j + 2k

а) 7 ;

б) 9;

в) 3;

г) 3 .

4. Если

для

a = (x ,

y , z

) и b = (x

, z

), тоa и b

а)ортогональны; б)компланарны;

в)коллинеарны;

г)равны.

5. Если для ненулевых векторов m n = 0 , то векторы m, n

а)равны;

б)ортогональны;

в)коллинеарны;

г)компланарны.

6. Площадь треугольника, построенного на

a и b находится по

формуле:

1 r

а) S =

×b; б) S

; в) S =

×b

;

г) S =

7*. Проекция вектора a(x1 , y1 , z1 )на направление вектора

b(x2 , y2 , z2 ) находится по формуле:

ar b

x1 x2 +

y1 y2 + z1

а) прra

;

б)

прra

;

x12 + y12 + z12

в) прrar

×r

;

г) прrar

= x1 x2 + y1 y2 + z1 z2 .

x22 + y22 + z22

8*. Если A(1, 0, − 3), B(5, 2,1), то координаты середины отрезка

AB равны

б) (6; 2; − 2);

в) (2,5; 0; −1,5);

(3;1; −1).

а) (2;1; 2);

г)

9*. Скалярное произведение векторов ar = 2i

− j

и b = rj − k

равно:

а) числу 5;

б) вектору c (2;1;-1);

в) числу –1;

г) числу 1.

Модуль 2. АНАЛИТИЧЕКАЯ ГЕОМЕТРИЯ § 1. Плоскость и ее основные уравнения

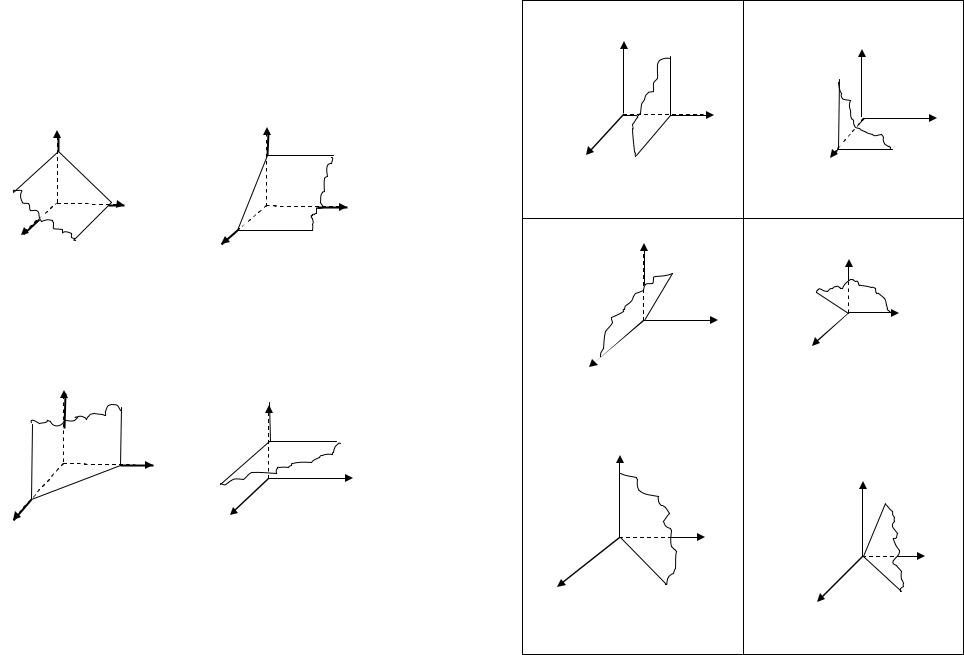
Рассмотрим плоскость P в прямоугольной декартовой системе координат. Положение плоскости вполне определяется точкой

M 0 (x0 , y0 , z0 ) P и вектором нормали nr = (A, B,C) P (nr ≠ 0) (рис. 2.1).

n = (A, B,C)

M1 P

хРис. 2.1

Возьмем любую точку M (x, y, z) P и построим вектор

M 0 M = (x − x0 , y − y0 , z − z0 ) . Так как nr M 0 M , то	скалярное
произведение nr M 0 M = 0, или
A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0.	(2.1)

Получили уравнение плоскости, заданной точкой M 0 (x0 , y0 , z0 ) и вектором нормали n = (A, B,C) .

Если	в	уравнении (2.1)	раскрыть скобки	и обозначить
D = −Ax0	− By0	− Cz0 , то получим общее уравнение плоскости:
	Ax + By + Cz + D = 0		(A2 + B2 + C 2	> 0) .	(2.2)

Теорема. Всякое уравнение вида (2.2) определяет некоторую плоскость в пространстве.

Если в уравнении (2.2) какой-либо из коэффициентов A, B,C равен нулю, то плоскость расположена параллельно той оси, координата

которой отсутствует в уравнении.		Например, при A = 0	плоскость
By + Cz + D = 0 параллельна	оси	Ox ; при A = B = 0	плоскость
C z + D = 0 параллельна осям	Ox и Oy , т.е. плоскости		xOy и т.д.
(табл. №1).

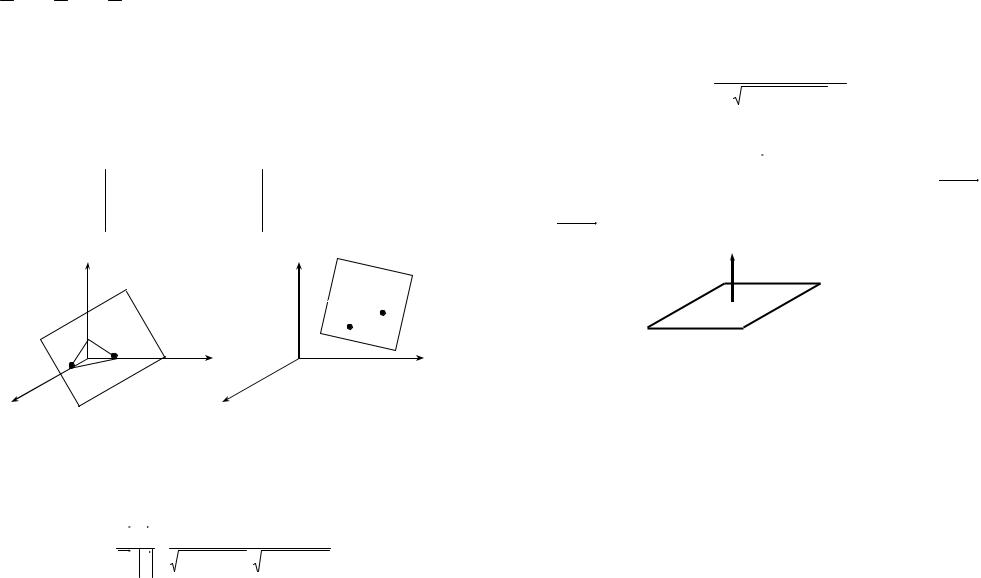
Частные случаи расположения плоскости, определяемой общим уравнением

Ax + By + Cz + D = 0 :

		Таблица №1
1. Плоскость параллельна оси Ох.		2. Плоскость параллельна оси Оy.
	Z	Z

Х	Y	Y
		Х
	А=0	B=0
Общее уравнение будет иметь вид:		Общее уравнение будет иметь вид:
By + Cz + D = 0		Ax + Cz + D = 0

3. Плоскость параллельна оси Оz.		4. Плоскость перпендикулярна оси
		Оz (параллельна плоскости xOy)
	Z

			Z
	Y
		Y
	Х
		Х
	C=0	А=В=0
Общее уравнение будет иметь вид:		Общее уравнение будет иметь вид:
	Ax + By + D = 0	Cz + D = 0

5. Плоскость перпендикулярна оси	6. Плоскость перпендикулярна оси
Оy (параллельна плоскости xOz).	Оx (параллельна плоскости yOz).
Z	Z
	Z

Y	Х	Y
Х	Х	Y
Х
А=С=0		С=В=0
Общее уравнение будет иметь вид:	Общее уравнение будет иметь вид:
By + D = 0		Ax + D = 0
7. Плоскость проходит через ось Ох	8. Плоскость проходит через ось Оy
Z		Z
Z

Y
Х		Х
Х		B=D=0
А=D=0		B=D=0
А=D=0	Общее уравнение будет иметь вид:
Общее уравнение будет иметь вид:	Общее уравнение будет иметь вид:
By + Cz = 0		Ax + Cz = 0

9. Плоскость проходит через ось Оz	10. Плоскость проходит через
Z	начало координат
Z
		Z
Y
Х		Y
Х
C=D=0	D=0	Х
Общее уравнение будет иметь	Общее уравнение будет иметь вид:
вид: Ax + By = 0		Ax + By + Cz = 0

Пусть в уравнении (2.2) ни один из коэффициентов A,B,C,D не равен 0. Перепишем уравнение (2.2) в виде Ax + By + Cz = −D , разделим обе части этого равенства на − D и обозначим

− DA = a, − DB = b, − CD = c .Получим уравнение плоскости в отрезках:

x	+	y	+	z	=1,	(2.3)
a		b		c

где a,b, c – это величины направленных отрезков, отсекаемых плоскостью на осях координат (рис. 2.2).

Если три точки M1 (x1 , y1 , z1 ) , M 2 (x2 , y2 , z2 ) , M 3 (x3 , y3 , z3 ) не лежат на одной прямой, то через эти точки проходит единственная плоскость (рис. 2.3). Уравнение плоскости, проходящей через три точки, имеет вид:

x − x1 x2 − x1 x3 − x1

y − y1 y2 − y1 y3 − y1

z − z1

z2 − z1 = 0. (2.4) z3 − z1

MM1

			M3
c			M3	M2
0	b	y	0
0	b	y	0
y
a
x			x
Рис. 2.2			Рис. 2.3
Пусть даны	две	плоскости P1 : A1 x + B1 y + C1 z + D1 = 0 и
P2 : A2 x + B2 y + C2 z + D2		= 0 . Угол ϕ	между двумя плоскостями

равен углу между их векторами нормали:

cosϕ= n1 n2 =				A1A2 +B1B2 +C1C2				.
	n	n	A2	+B2	+C2	A2	+B2	+C2
	1	2	1	1	1	2	2	2

При этом

P1 P2

A1 A2 + B1B2

+ C1C2 = 0 (условиеперпендиулярности

плоскостей),

P || P

(условие параллельности плоскостей).

Расстояние

от

точки M1 (x1 , y1 , z1 )

до плоскости

Ax + By + Cz + D = 0 определяется по формуле

d =

| Ax1 + By1 + Cz1 + D |

A2 + B 2 + C 2

Пример 2.1. Даны две точки

M1 (−2, 0,1)

M 2 (1, 4, 2) . Записать

уравнение

плоскости,

проходящей

через

точку

перпендикулярно вектору M1M 2 .

Решение. Поскольку искомая плоскость перпендикулярна

M1M 2 ,

то

качестве

вектора

нормали

возьмем

вектор

M1M 2 = (3, 4,1) (рис.2.4).

М2

М1

Рис. 2.4

Подставив теперь в уравнение A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0

A = 3,	B = 4, C =1	, а также	координаты точки	M1 :
x0 = −2,	y0 = 0, z0	=1, получим уравнение
3(x + 2) + 4( y		− 0) +1(z −1) = 0	или 3x + 4y + z + 5 = 0

– это и есть искомое общее уравнение плоскости.

Пример 2.2. Найти величины отрезков, которые отсекает плоскость 2x − 3y + 4z −12 = 0 на осях координат.

Решение. Преобразуем уравнение плоскости:

2x − 3y + 4z =12 ,

−

=1 ,

−

=1.

Получили уравнение плоскости в отрезках (см. 2.3). Следовательно, данная плоскость отсекает на осях координат отрез-

ки a = 6, b = −4, c = 3.

Пример 2.3. Записать уравнение плоскости, проходящей через точки A(1, 2, − 3), B (−1, 6,1), C(4, 8, − 9).

Решение. Подставляя в уравнение (2.4) координаты точек A, B,C ,

получим уравнение:
	x −1	y − 2 z + 3			x −1 y − 2 z + 3
	x −1	y − 2 z + 3			x −1 y − 2 z + 3
	−1 −1	6 − 2	1 + 3	= 0 или	− 2	4	4	= 0 .
	4 −1	8 − 2	− 9 + 3		3	6	− 6

Разложив определитель по элементам первой строки, получим искомое уравнение плоскости:

(x −1)

− (y − 2)

− 2 4

+ (z + 3)

− 2

= 0,

− 6

− 48(x −1)−

(y −

2)− 24(z

+ 3)= 0,

или 2(

x −1)+

(z + 3)= 0,

2x − 2 + z − 3 = 0,

2x + z − 5 = 0.

§ 2. Прямая в пространстве и ее основные уравнения

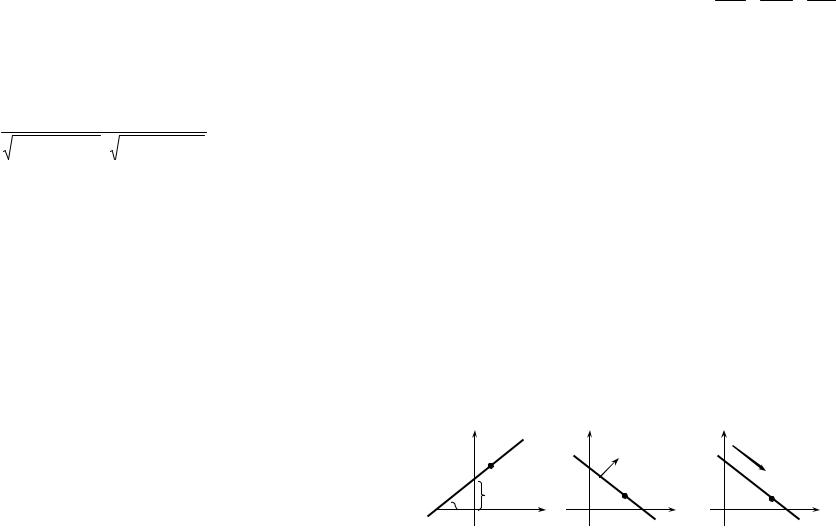
Рассмотрим прямую l в прямоугольной декартовой системе координат. Положение прямой в пространстве вполне определяется точкой M 0 (x0 , y0 , z0 ) l и направляющим вектором

s = (m, n, p) || l (sr ≠ 0) (рис. 2.5).

s = (m, n, p)

M l

Рис. 2.5

Возьмем любую точку M (x, y, z) l и построим вектор M 0 M || sr , из условия коллинеарности этих векторов получим

канонические уравнения прямой в пространстве:
	x − x0	=	y − y0	=	z −z 0	.	(2.5)
	m		n
					p

Обозначим в (2.5) коэффициент пропорциональности через t и выразим через t переменные x, y, z . Приходим к параметрическим

уравнениям прямой в пространстве:

x = x0

+ mt,

+ nt,

– параметр.

(2.6)

y = y0

+ pt,

z = z0

Уравнение прямой, проходящей через две точки M1 (x1 , y1 , z1 )

M 2 (x2 , y2 , z2 ) , имеет вид:

x − x1

y − y1

z −z1

(2.7)

− x

− y

−z

Рассмотрим две

плоскости

P1 :

A1 x + B1 y + C1 z + D1

= 0

P2 : A2 x + B2 y + C2 z + D2 = 0 . Если эти плоскости не параллельны, то они пересекаются по прямой, задаваемой системой уравнений:

A x

+ B y + C z +

= 0,

(2.8)

A2 x + B2 y + C2 z + D2 = 0.

Система

(2.8)

называется

общими

уравнениями прямой в

пространстве.

Направляющий вектор s

прямой (2.8) можно найти по формуле

sr = nr1 × nr2 =

Угол ϕ между двумя прямыми l1

и l2

равен углу между их

направляющими векторами s1

= (m1 , n1 , p1 ) и s2 = (m2 , n2 , p2 ) :

s1 s2

m1m2 +n1n2 + p1 p2

cosϕ=

| sr1 || sr2 | =

m12 +n12 + p12

m22 +n22 + p22 .

При этом

l1 l2

m1m2

+ n1n2 + p1 p2 = 0

(условие перпендиулярности

прямых),

l || l

(условие параллельности прямых).

Угол ψ между прямой

x − x0

y − y0

z −z 0

и плоскостью

Ax + By + Cz + D = 0 определяется по формуле

sin ψ =

| Am + Bn + Cp |

A2 + B2 + C 2

m2 + n2 + p2 .

При этом

l || P

Am + Bn + Cp = 0

(условие параллельности прямой и

плоскости),

l P

(условие перпендиулярности прямой и

плоскости). Пример 2.4. Составить канонические и параметрические уравнения

прямой, проходящей через точки M1 (3, 2, −1) и M 2 (4, 2,1) .

Решение. Подставляем в формулу (2.7) координаты точек

M1 и

M 2 :

x − 3

y − 2

z +1

4 − 3

2 − 2

1 +1

или

x − 3

y − 2

z +1

– канонические уравнения прямой (нуль в

знаменателе означает, что направляющий вектор s = (1, 0, 2)

пер-

пендикулярен оси Oy , т.е. прямая перпендикулярна оси Oy ).

Запишем параметрические уравнения прямой:

x − 3

y − 2

z +1

= t

x − 3 = t,

y − 2 = 0, z +1 = 2t,

x = 3 + t, y = 2, z = −1 + 2t .

Пример 2.5. Проверить, являются ли прямая x 3− 3 = y 2− 2 = z−+11 и

плоскость 6x + 4y − 2z + 5 = 0 а) параллельными; б) перпендикуляр-

ными. r Решение. Запишем координаты направляющего вектора s прямой

и вектора нормали n плоскости: s = (3; 2; −1), n = (6, 4, − 2 ).

а) прямая параллельна плоскости, если s n s n = 0 . s n = 3 6 + 2 4 + (−1) (− 2)=18 +8 + 2 = 28 ≠ 0.


Следовательно, прямая и плоскость не параллельны.
б) прямая перпендикулярна плоскости, если s \|\| n ,							то есть коорди-
наты векторов пропорциональны.
Так как	6	=	4	=	− 2	= 2 , то прямая и плоскость перпендикулярны.
	3		2
					−1
§ 3. Прямая на плоскости и ее основные уравнения
Уравнение прямой с угловым коэффициентом k							имеет вид
					y = kx + b или y − y0 = k(x − x0 ) ,

где k = tgα – угловой коэффициент прямой,					b
отсекаемого этой прямой на оси Oy ,				(x0 , y0 )
прямой (рис. 2.6).
y		y			y
l			n = (A, B)
M0(x0, y0)			M0(x0, y0)
b			M0(x0, y0)
α	x		l	x
0	x	0	l	x	0
Рис. 2.6			Рис. 2.7

–величина отрезка,

–точка, лежащая на

s = (m, n)

M0(x0, y0)

l x

Рис. 2.8

Кроме того, прямую l на плоскости можно задать вектором нормали n = (A, B) l и точкой M 0 (x0 , y0 ) l (рис. 2.7). Получим 3 уравнения, аналогичные уравнениям (2.1) – (2.3) для плоскости:

A(x − x0 ) + B( y − y0 ) = 0 – уравнение прямой, заданной точкой и вектором нормали;

Ax + By + C = 0 – общее уравнение прямой;

ax + by =1 – уравнение прямой в отрезках.

Прямая l на плоскости также определяется направляющим вектором s = (m, n) || l и точкой M 0 (x0 , y0 ) l (рис. 2.8). Получим еще 3 уравнения, аналогичные уравнениям (2.5) – (2.7) прямой в пространстве:

x −mx0 = y −ny0 – каноническое уравнение прямой;

x = x0			+ mt,			– параметрические уравнения прямой;
			+ nt
y = y0
x − x1			=	y − y1			– уравнение прямой, проходящей

x	2	− x		y	2	− y
		1				1

через две точки M1 (x1 , y1 ) и M 2 (x2 , y2 ) .

Угол ϕ

между

двумя

прямыми,

заданными

уравнениями:

l1: y = k1 x + b1

l2:

y = k2 x + b2

можно найти по формуле

tgϕ =

k2 − k1

;

при этом

+ k1 k2

k k

= −1, т.е. k

= −

(условие

l1 || l2

k1 = k2

перпендиулярности прямых),

(условие параллельности прямых).

Расстояние d

от точки M1 (x1 , y1 )

до прямой

Ax + By + C = 0

вычисляется по формуле

| Ax1 + By1

+ C |

d =

A2 + B2

Пример 2.6. Записать уравнения прямых, проходящих через точку M(– 2, 1) параллельно и перпендикулярно прямой 3x − 4y +12 = 0 .

Решение. Перепишем общее уравнение					прямой 3x − 4y +12 = 0
(l) , выразив из него переменную y :				l :	y =	3	x +	3 .
(l) , выразив из него переменную y :				l :	y =	4	x +	3 .
		y				4
l2		y
l2		l	l1
	M	1			х
-4	–2	0			х

Рис. 2.9

Получили уравнение прямой с угловым коэффициентом k = 34 . За-

пишем уравнение прямой l1 || l и проходящей через точку M(– 2, 1). Поскольку для параллельных прямых угловые коэффициенты

равны, т.е. k1 = k = 34 , то

l1 : y −1 = 34 (x + 2) или

4y − 4 = 3x + 6,

3x − 4y +10 = 0.

Составим уравнение прямой l2 l , проходящей через точку M(– 2,1). Так как угловые коэффициенты перпендикулярных

прямых связаны соотношением k2 = − 1k = − 43 , то

l2 : y −1 = −	4	(x + 2) или
l2 : y −1 = −	3	(x + 2) или
	3
3y − 3 = −4x −8,		4x + 3y + 5 = 0.

Прямые l, l1 , l2 изображены на рис. 2.9.

§ 4. Кривые второго порядка

Кривой второго порядка называется линия, уравнение которой в декартовой системе координат имеет вид

Ax2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0,

(2.9)

где коэффициенты А, В, С одновременно не обращаются в нуль. При А = В = С = 0 уравнение (2.9) задает прямую, которая назы-

вается линией первого порядка.

К числу линий второго порядка относятся окружность, эллипс, гипербола и парабола.

1. Окружностью называется множество точек плоскости, равноудаленных от данной точки (центра).

Если центр окружности поместить в начало координат, то ка-

ноническое уравнение окружности радиусом R имеет вид

x2 + y2 = R2 .

Если центр окружности находится в точке C(x0 , y0 ) , то ее уравнение записывается в виде

(x − x0 )2 + ( y − y0 )2 = R2 .

Эта окружность изображена на рис. 2.10.

2. Пусть на плоскости заданы две точки F1 и F2 , расстояние между которыми равно 2с, и задано число a > c.

Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек F1 и F2 (фокусов) есть

величина постоянная, равная 2а.

Если систему координат выбрать так, как указано на рис.2.11,

то каноническое уравнение эллипса запишется в виде

x2	+	y 2	=1,
a 2		b2

где b2 = a2 − c2 , а – большая, b – малая полуоси эллипса (при a>b).

Фокусы эллипса расположены в точках F1 (−с,0) и F2 (c,0) . Окружность есть частный случай эллипса при a = b.

3. Пусть на плоскости заданы две точки F1 и F2 , расстояние между которыми равно 2с, и задано число a < c.

Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до двух данных точек F1 и F2

(фокусов) есть величина постоянная, равная 2а.

Если систему координат выбрать так, как указано на рис. 2.12,

то каноническое уравнение гиперболы запишется в виде

x2	−	y 2	=1,
a2		b2

где b2 = c2 − a2 , а – действительная, b – мнимая полуоси гипербо-

лы.

Гипербола состоит из двух ветвей и расположена симметрично относительно координатных осей. При этом ее ветви при удалении в

бесконечность как угодно близко подходят к прямым y = ± ba x, ко-

торые называются асимптотами гиперболы.

При построении гиперболы вначале строят основной прямоугольник со сторонами x = ±a, y = ±b . Затем через противополож-

ные вершины этого прямоугольника проводят прямые, которые являются асимптотами гиперболы. Вершины гиперболы расположены в точках с координатами (–а,0) и (а,0), а фокусы – в точках F1 (−с,0)

иF2 (c,0) (рис. 2.12).

Уравнение

−

y 2

= −1 (или −

y 2

=1 ) также задает ги-

перболу, сопряженную с гиперболой

−

y 2

=1. Действительная и

мнимая полуоси этой гиперболы соответственно равны b и а.

4. Пусть на плоскости задана точка F и прямая D, расстояние между которыми равно р.

Параболой называется множество точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой D (директрисы).

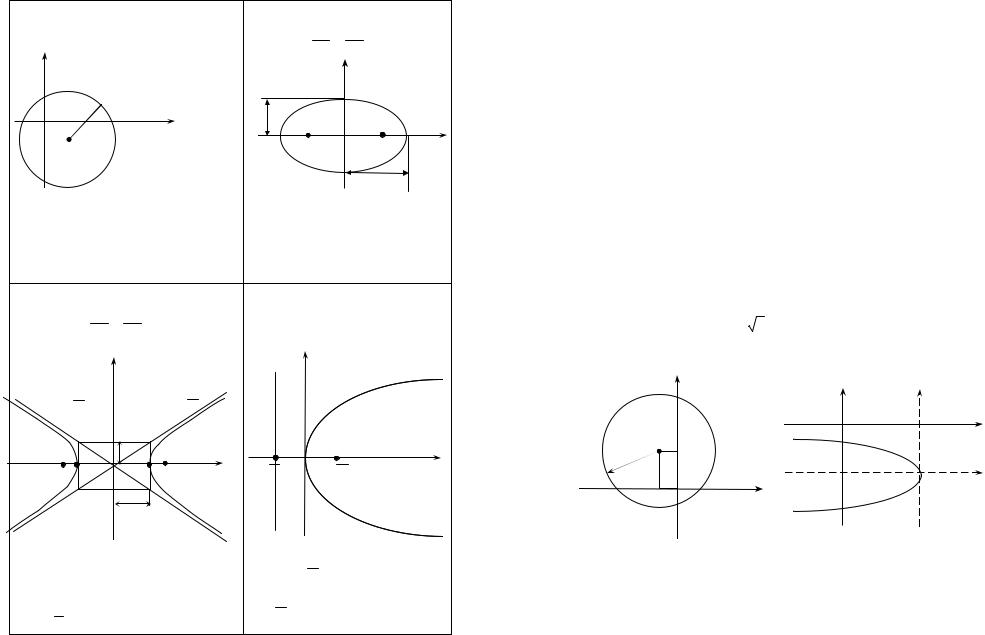
Кривые второго порядка

Таблица №2

Окружность

Эллипс

(x − x0 )2 + ( y − y0 )2 = R2

y 2

a 2

+ b2

− c

C(x0, y0)

R - радиус окружности,

a - большая полуось,

b - малая полуось,

C(x0 , y0 )

- центр окружности.

F1 (−c,0), F2 (c,0)

- фокусы,

Рис. 2.10

= a2 − b2 .

Рис. 2.11

Гипербола

Парабола

−

y 2

y 2 = 2 px ( p > 0)

y = − b

= b

−c

−

a - действительная полуось,

р – параметр параболы,

b - мнимая полуось, c2 = a2 +b2 ,

D : x = − p - директриса,

F1 (−c, 0), F2 (c, 0) - фокусы,

y = ± b x - асимптоты

Рис. 2.12

F( 2

,0) - фокус.

Рис. 2.13

Если систему координат выбрать так, как указано на рис.2.13, то

каноническое уравнение параболы запишется в виде y 2 = 2 px.

Эта парабола симметрична относительно оси Ох. Директрисой яв-

	x = −	p		p
ляется прямая			, точка	F		,0 – фокус параболы, р – пара-
		2			2

метр параболы.

Если p < 0, то парабола направлена в противоположную сторону.

Уравнение x2 = 2 py задает параболу, симметричную относительно оси Оу.

Для того, чтобы построить кривую второго порядка, заданную общим уравнением, уравнение кривой приводят к каноническому виду и переходят к новой системе координат.

Пример	2.7. Определить тип кривой, заданной уравнени-
ем(x +1)2	+ (y − 2)2 = 9 и построить ее.

Решение. Данное уравнение задает окружность с центром в точке

C(−1; 2)

и радиусом

R = 9 =3 . Окружность изображена на рис.

2.14.

2,5

С(-1;2)

R=3

-1,5

-1

Рис. 2.14

Рис. 2.15

Пример 2.8. Определить тип линии и схематически построить ее: 2y 2 + x + 6y + 2 = 0.

Решение. Перепишем уравнение в виде

2( y 2 + 3y) + x + 2 = 0

и выделим полный квадрат:

2 y

+ 2

−

+ x

+ 2 = 0,

2 y +

−

+ x

+ 2

= 0, y +

= −

−

Совершим параллельный перенос по формулам

X = x −

, Y = y +

Координаты нового центра О

,−

. Уравнение примет вид

Y 2 = − 1

X .

Это

каноническое

уравнение

параболы

вида

Y 2

= 2 pX , где

p = −

< 0 .

Поэтому

парабола

направлена

отрицательную

сторону оси О1X .

Парабола изображена на рис. 2.15.

Пример

2.9.

Построить

гиперболу,

заданную

уравнением

−

=1.

Найти

ее

полуоси,

координаты

фокусов

записать

уравнения ее асимптот.

Решение. Данное уравнение является каноническим уравнением

вида	x2	−	y 2	=1.	Поэтому	действительная	полуось
	a 2		b2

a = 25 = 5, мнимая полуось b = 9 = 3 . Найдем координаты фоку-

сов F1 и F2: c = a2 + b2 = 25 + 9 = 34 , F1 (− 34 , 0), F2 ( 34; 0).

Уравнения асимптот гиперболы имеют вид y = ± 53 x .

Построение гиперболы начинаем с построения основного прямоугольника со сторонами 2a=10 и 2b=6, параллельными осям координат. Асимптоты гиперболы проходят по диагоналям этого пря-

моугольника. Вершины гиперболы расположены в точках пересечения основного прямоугольника с осью oХ.

Гипербола изображена на рис. 2.16.

-5 О 5 x

-3

Рис. 2.16

§ 5. Поверхности второго порядка

Рассмотрим в плоскости xOy эллипс, гиперболу, сопряженную

гиперболу, параболу и пару пересекающихся прямых. Совершим вращение этих линий вокруг оси Oy и деформацию(сжатие или

растяжение) образованных таким образом поверхностей второго порядка. Эти поверхности со своими каноническими уравнениями изображены на рис. 2.17 - 2.21.

Если в уравнении эллиптического параболоида поменять знак, то придем к уравнению, которое задает гиперболический параболоид (седло), изображенный на рис. 2.22.

Цилиндрической поверхностью называется поверхность, которая образуется при поступательном перемещении некоторой линии (образующей) вдоль некоторой кривой (направляющей). Выбирая в качестве направляющей эллипс, гиперболу и параболу, расположенные в плоскости xOy , а в качестве образующей – прямую, парал-

лельную оси Oz , получим соответственно эллиптический, гипербо-

лический и параболический цилиндры, изображенные на рис. 2.23 - 2.25.

При построении поверхностей второго порядка часто пользуются таблицей этих поверхностей (см. табл. №3), учитывая, что ось фигуры или образующая может быть параллельна не только оси Oz .

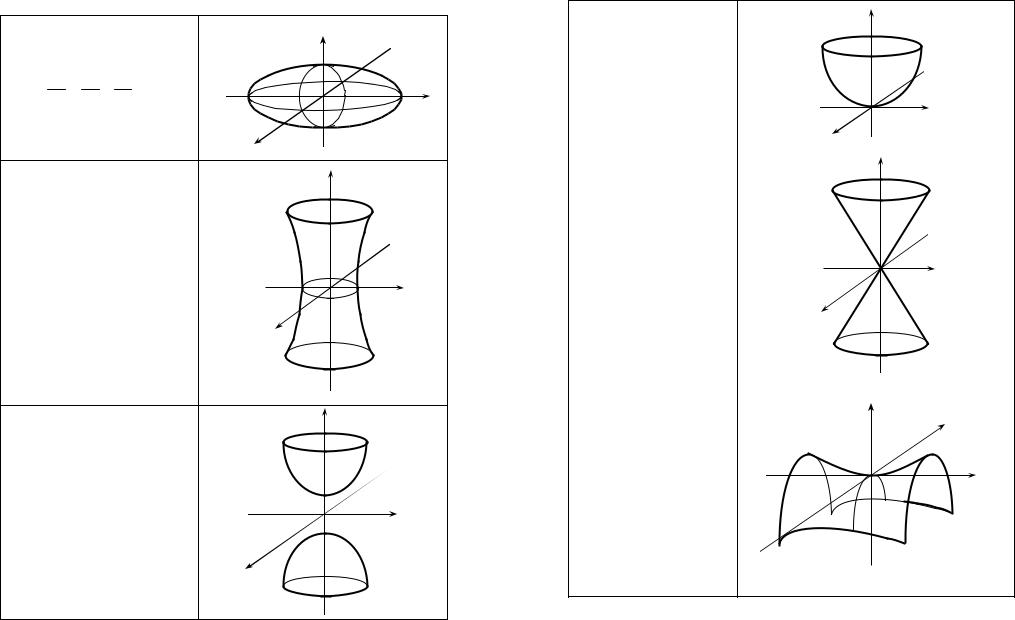
Поверхности второго порядка

							Таблица №3
	Эллипсоид					z	c
	Эллипсоид						c
x2	+	y 2	+	z 2	=1	o	b
a2	+	b2	+	c2	=1	o	b
a2		b2		c2		a	y

Рис. 2.17 x

Однополостный

гиперболоид

x2	+	y 2	−	z 2	=1
a 2	+	b2	−	c2	=1		o	b
a 2		b2		c2			o	b
							a	y
							a
						x

Рис. 2.18

Двуполостный

гиперболоид

x2	+	y 2	−	z 2	= −1	o с
a2		b2		c2		-с
a2		b2		c2		-с	y
						x
						x
					Рис. 2.19

Эллиптический

параболоид

x2	+	y 2	= 2z
a2	+	b2	= 2z	o
a2		b2

			x	y
			x
			Рис. 2.20

				z

Конус второго порядка

x2	+	y 2	−	z 2	= 0	o
a2		b2		c2
							y

						x

				Рис. 2.21
Гиперболический					z	y
параболоид					z
параболоид
(седло)
	x2		y 2		o	x
	x2		y 2
	a2	− b2 = 2z
	a2	− b2 = 2z

Рис. 2.22

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.09.201983.46 Кб11Макр. Нестаб. (2).doc
#
13.09.2019303.62 Кб8Макроэк. равновесие в класс.мод.. 2.doc
#
22.02.2016521.22 Кб24Макроэк.равн. IS-LM.doc
#
01.04.2025132.87 Кб0маркетинг 2.docx
#
22.02.2016828.42 Кб65МАРКЕТИНГ.doc
#
22.02.20161.03 Mб23Математика. Часть 1.pdf
#
22.02.20163.92 Mб141Материаловедение_лабараторный практикум.pdf
#
22.02.20163.92 Mб64Материаловедение_лабпракт.pdf
#
22.02.2016959.49 Кб73Материалы - Менеджмент (ТОМ) - 17-24зэи.doc
#
22.02.2016334.34 Кб39Материалы к ГЭК 2012.doc
#
22.08.2019272.9 Кб7материалы по преддипл. практике рем 2012 год..doc