Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный аграрный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика. Часть 1

.pdf

Скачиваний:

Добавлен:

22.02.2016

Размер:

1.03 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Пример 2.10. Определить тип поверхности, задаваемой уравнением

x2 − 2y 2

+ z 2 =1.

Решение. Это каноническое уравнение

однополостного

гипербо-

Эллиптический

лоида, у которого осью симметрии является ось Oy (перед y 2 стоит

цилиндр

знак “-”). Поверхность представлена на рис. 2.26.

Рис. 2.23

Гиперболический

цилиндр

Рис. 2.26

Рис. 2.27

−

y 2

Пример

2.11. Построить поверхность,

задаваемую уравнением

y 2 + 2z 2

= 4.

Рис. 2.24

Решение. Перепишем уравнение в виде

=1. Это канониче-

ское уравнение эллиптического цилиндра,

образующая

которого

параллельна оси Ox . Поверхность изображена на рис. 2.27.

Параболический

цилиндр

= 2 py

Рис. 2.25

ЗАДАЧИ ДЛЯ УПРАВЛЯЕМОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ

1. Даны две точкиM1 (2,−1,3) и M 2 (3,2,1) . Составить уравнение плоскости, проходящей через точку М, перпендикулярно вектору

M1M 2 .

2. Записать уравнение прямой, проходящей через точку M1 (2,0,5) перпендикулярно плоскости α : 2y − z +1 = 0 .

3. Даны вершины пирамиды A(−1; − 2; −8), B(0; − 4; − 6),

C(10; 0; 2), D(7; 2; 0).

1)записать уравнение ребра AD ;

2)записать уравнение грани ABC ;

3) найти угол между ребром AD и гранью ABC .

4.По данным координатам вершин треугольника ABC A(−2;−3), B(10;−12), C(14;10) составить уравнение медианы АМ.

5.Написать уравнение прямой, проходящей через точку M (1; 2) перпендикулярно прямой 3x − 5y +1 = 0 .

6.Определить вид и построить кривые второго порядка

а)

y 2

=1;

б)

−

y 2

=1;

в) x − 2 = y

7.Найти координаты центра и радиус окружности, заданной уравнением x2 − 4x + y 2 = 0 .

8.Составить уравнение окружности с центром в точке S (5,6) и проходящий через точку M (7,3) . Построить окружность.

9.Составить уравнение линии на плоскости, для которой отношение расстояний до данной точки F (2,0) и расстоянию до данной

прямой x = −2 равно числу ε =3 . Полученное уравнение привести к каноническому виду и построить кривую.

КОНТРОЛЬНЫЙ ТЕСТ ПО МОДУЛЮ №2

10. В уравнении плоскости Ax + By + Cz + D = 0 коэффициенты A, B, C задают:

а) координаты направляющего вектора ; б) координаты нормированного вектора;

в) точки, через которые проходит плоскость; г) координаты вектора нормали.

20. Канонические уравнения прямой в пространстве имеют вид:

x − x

y − y

z − z

а)

;

б)

Ах

+ By + Сz = 0 ;

x = x0

+ mt

=1 .

в) y = y0

+ nt ;

г)

+ pt

z = z0

30. Уравнение вида		x	+	y	+	z	=1 называется:
		a		b		c

а) уравнением плоскости в отрезках;								б) общим уравнением;
в) каноническим;								г) нормальным.

40. Центр окружности (x + 4)2							+ (y −1)2	= 25 находится в точке:
а) С1 (4,1);	б) С2 (− 4, −1);						в) С3 (− 4,1);		г) С4 (−1, − 4).
5. Плоскость с уравнением 3х + 4y + z = 0 проходит:
а) через начало координат;							б) параллельно оси Ox ;
в) параллельно плоскости xOy ; г) параллельно оси Oz .
6. Прямая 3x + 2 y = 6 отсекает на оси Oy отрезок, равный:
а)2;	б) 3;						в) 1;		г)-3.

7. Условие параллельности двух прямых на плоскости,					заданных
уравнениями:	y = k1 x + b1 , y = k2 x + b2
а) k1 k2 = 0 ;	б) k1 = k2 ;	в) k1 k2 =1;		г) k1 k2 = −1.
8. Тангенс угла наклона прямой y =3x − 5 к положительному
направлению оси Ox равен:
а) 3;	б) 5;		в) –5;		г) 1.
9. Уравнение плоскости, прoxодящей через три точки
A(a1 , a2 , a3 ) ,	B(b1 , b2 , b3 ) , C(c1 , c2 , c3 )		имеет вид:

а)

в)

x − x1

y − y1

z − z1

= 0 ;

− x

− y

− z

x3 − x1

y3 − y1

z3 − z1

Ax + By + Cz + D = 0 ;

г)

б)

x − a1

y − a 2

z − a3

= 0 ;

− a

− a1

− a 2

− a3

А(х − а) + В( у − b) + C(z − c) = 0 .

10. Уравнение эллипса имеет вид:

а)

−

y 2

=1;

б)

x 2

y 2

+ c 2 = 0 ;

a 2

b 2

в) x

− y

= a

;

г)

y 2

=1.

11. Укажите уравнение эллиптического параболоида

а)

y 2

=1 ;

б)

x 2

z 2

= 2y ;

a 2

c 2

в) x

= 2y ;

г)

y 2

−

z 2

= 0 .

12*.

Плоскости с

уравнениями

2х + y + 3z −1 = 0

4x + 2y + 6z + 5 = 0 являются:

а) перпендикулярными ;

б) параллельными;

в) совпадающими.

г) скрещивающимися

13*. Уравнение прямой, проходящей через начало координат и точку М(1,2) имеет вид:

а)

;

б)

= 0 ;

в)

;

г)

−

= 0 .

14*. Уравнение данной параболы имеет вид:

а) x − x0 = 2 p(y − y0 );

б) (x − x0 )2 = 2 p(y − y0 );

в) (y − y0 )2 = 2 px ;

г) (y − y

= 2 p(x − x

15*.Какая поверхность определяется уравнением −

−

=1?

б)

в)

г)

Модуль 3. ВВЕДЕНИЕ В АНАЛИЗ § 1. Понятие функции. Способы задания функций

Пусть X — некоторое множество действительных чисел. Определение. Если каждому элементу x из множества X по

некоторому закону f ставится в соответствие вполне определенное действительное число y , то говорят, что y есть функция переменной величины x и пишут y = f (x) .

Множество X называется областью определения функции f (x)

и обозначается D( f ) . Множество всех значений y функции y = f (x) , когда x пробегает всю область определения, называется

областью изменения или областью значений функции и обозначается

E( f ) .

Например, для функции y = sin x область определения D( f ) = R , область значений E( f ) =[−1;1] .

Различают следующие способы задания функции: табличный, графический, аналитический (с помощью формул).

Под графиком функции понимают множество точек плоскости, абсциссы которых есть значения независимой переменной, а ординаты равны соответствующим значениям функции. График фукции есть

некоторая линия на плоскости. Например, уравнение y = x2 задает функцию, графиком которой является парабола.

Косновным элементарным функциям относятся:

1.y = xa (при постоянном a R ) — степенная функция;

2.y = a x (при постоянном a R , a > 0 , a ≠1 ) —

показательная функция; 3. y = loga x (припостоянном a R , a > 0 , a ≠1 ) —

логарифмическая функция; 4. y = sin x, y = cos x, y = tgx, y = ctgx —

тригонометрическиефункции; 5. y = arcsin x, y = arccos x, y = arctgx, y = arcctgx —

обратныетригонометрическиефункции. Функция, заданная последовательной цепью нескольких функций ( y = f (u) , где u = ϕ(x) ), называется сложной функцией. Например,

функция y = lg3 (2x5 ) сложная, и она может быть представлена следующей цепью основных элементарных функций: y = z3 , z = lg u, u = 2v , v = x5 .

Функции, образованные из основных элементарных функций посредством конечного числа алгебраических операций и взятия функции от функции, называются элементарными. Все остальные

функции называются неэлементарными. Функция y = x2 sin x + 2x log4 x + 5

является элементарной. Примером неэлементарной функции может

служить функция вида y =1+x +x2 +x3 +...+xn +...

Функция

y = f (x)

называется четной (нечетной) функцией, если

для

любого

x D( f )

число

(− x) D( f )

и справедливо равен-

ство f (−x) = f (x)

(f (−x) = − f (x)). Например функция

y =

x2 − 4

является четной, функция y =

является нечетной. А функция

x2 − 4

y =

не является ни четной ни нечетной, так как ее область

оп-

x − 4

D(f )= (− ∞, 4) (4,+∞) не симметрична относительно на-

ределения

чала координат.

y = ϕ(t),

Функция,

определяемая

уравнениями

которых

зависимость между y

и x

x = ψ(t),

устанавливается посредством третьей

переменной

t , называется

заданной

параметрически,

при

этом

t —параметр.

Например,

уравнения

y = 2t +1,

x = t − 2

определяют линейную функцию y = 2(x + 2) +1 = 2x + 5 .

§ 2. Предел числовой последовательности. Предел функции

Определение.

Число A называется пределом последователь-

ности a1 , a2 ,..., an ,... если для любого положительного числа ε существует такой номер N = N (ε) , что при всех n > N выполняется неравенство an − A < ε .

Если последовательность a1 , a2 ,..., an ,... имеет своим пределом

число	A ,	то	это	записывается	следующим	образом
lim an = A или an			→ A при n → ∞.
n→∞
Определение. Число А называется пределом функции y = f ( x )
при x → a (в точке x = a ),				если для каждого числа ε > 0		найдется
такое число		δ = δ(ε) > 0 , что для любого			x D( f ) и удовлетво-

ряющего		неравенству 0 <	x − a	< δ выполняется	неравенство
ряющего		неравенству 0 <	x − a	< δ выполняется	неравенство
	f ( x ) − A	< ε. Обозначают этот факт так: lim f (x) = A .
	f ( x ) − A	< ε. Обозначают этот факт так: lim f (x) = A .
				x→a
				x→a
	Если	число A является пределом функции			y = f (x) при

x → a , то на графике это иллюстрируется следующим образом. Так как из

неравенства 0 < x − a < δ следует неравенство f (x) − A < ε , то это

значит, что для всех	x ,	отстоящих от a не далее чем на δ , точка
M графика функции	y = f (x) лежит внутри полосы шириной 2ε ,
ограниченной прямыми		y = A − ε и y = A + ε. Очевидно, что с

уменьшением ε величина δ также уменьшается (см. рис.3.1). y

		y = f (x)
A +ε
A	M	2ε
A −ε
0	a −δ a	a +δ	x

Рис.3.1

Число

называется пределом функции

y = f (x)

при x → ±∞ ,

если для

любого ε > 0 существует число

M > 0 ,

что при всех

> M выполняется неравенство

f (x) − A

< ε .

Функция

y = f (x) называется ограниченной в области D, если

существует

постоянное

число

M > 0 ,

что для

всех x D

выполняется неравенство

f (x)

< M .

Например, функция	y =	2	ограничена для всех x R , так
		+ x2
	1

как в этой области f (x) ≤ 2 .

§ 3. Бесконечно малые и бесконечно большие функции

Определение. Функция α(x) называется бесконечно малой при

x → a , если lim α(x) = 0 .

x→a

Функция β(x) называется бесконечно большой при x → a , если

lim β(x) = ∞ .

x→a

Например, функция

y =sin x является бесконечно малой при

x → 0 , а функция y =

есть бесконечно малая при x → ±∞ ,

y = tgx

так как их пределы

равны нулю. Функция

является

бесконечно малой при x → 0

и бесконечно большой при

x →

π .

Теорема.

Если функция α(x) — бесконечно малая

при

x → a ,

то

— бесконечно большая функция при x → a

=∞ .

α(x)

Если функция β(x)

— бесконечно большая при x → a , то

β(x)

- бесконечно малая функция при x → a ( ∞1 = 0 ). (Доказательство см. [1], гл. II, §4.). Справедливы следующие утверждения:

1.Сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2.Произведение ограниченной функции на бесконечно малую есть бесконечно малая функция.

3.Произведение конечного числа бесконечно малых функций есть бесконечно малая функция.

§ 4. Теоремы о пределах

Если пределы limu(x) и lim v(x)				существуют и конечны, то
	x→a	x→a
1.	lim cu(x) = c lim u(x) , где с – const;
	x→a		x→a
2.	lim(u(x) + v(x)) = limu(x) + lim v(x) ;
	x→a			x→a		x→a
3.	lim(u(x) v(x)) = lim u(x) lim v(x) ;
	x→a			x→a		x→a
	lim u(x)		lim u(x)
4.		=	x→a		, где lim v(x) ≠ 0 .
4.		=	lim v(x)		, где lim v(x) ≠ 0 .
	x→a v(x)		lim v(x)			x→a
			x→a

Замечательные пределы.

Первый замечательный предел: lim sin x =1 .

x→0 x

Второй замечательный предел:

1 x

= lim (1 + x )

lim

1 +

= e ,

x→∞

где e — иррациональное

число, e ≈ 2,718281828

— одна

из

фундаментальных величин в математике. Функция

y =ex =exp(x)

называется экспонентой;

y = loge x = ln x называется натуральным

логарифмом.

Пример 3.1. Вычислить lim

−3x + 3

+ x − 3

x→2

Решение. Так как

lim(x2

+ x − 3) = lim x2

+ lim x − 3 = 3 ≠ 0 ,

то

x→2

применима теорема о пределе частного. Значит,

x2 − 3x + 3

lim(x2

− 3x + 3)

lim

x→2

+ x − 3

lim(x2

+ x − 3)

x→2

Пример 3.2. Вычислить lim

2x3 −3x2 +1

x3 + 4x −

x→∞

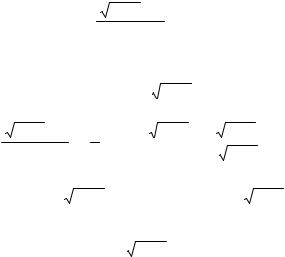
Решение. Так как при x → ∞ числитель и знаменатель дроби, стоящей под знаком предела, стремятся к бесконечности, то имеем

неопределенность вида ∞∞ . Для раскрытия таких неопределенностей

делят числитель и знаменатель дроби на старшую степень x . После деления на x3 получаем:

2x3 −3x2

2 −

2 − 0 + 0

lim

= lim

= 2 .

1 + 0 − 0

x→∞

x3 + 4x − 2

x→∞

1 +

−

Пример 3.3. Вычислить lim

+ x −12

x2 −

x→3

Решение.

Так

как lim(x2 + x −12) = 0 и lim(x2 − 9) = 0 , то

имеем

x→3

неопределенность

вида

0 .

Разложим числитель и

знаменатель

дроби на линейные множители. Так как x2

+ x −12 = 0 при x

= 3 и

x2 = −4 ,

то

x2 + x −12 = (x −3)(x + 4);

x2 −9 = (x −3)(x + 3) .

Тогда lim

x2 +x−12

=lim

(x−3)(x

+4)

=lim

x2 −9

+3)

x→3

x→3 (x−3)(x

x→3 x

Пример 3.4. Вычислить lim

x + 7 − 3 .

x→2

x2 − 3x + 2

Решение. Имеем неопределенность вида

. Умножим числитель и

знаменатель дроби на выражение (						x + 7 + 3 ),	а так же разложим
знаменатель на линейные множители:							x + 7 + 3)
	x + 7 −3		0	= lim	(	x + 7 −3)(		=
lim		=
	x2 −3x + 2				(x −1)(x − 2)(		x + 7 + 3)
x→2			0	x→2

= lim

x + 7 − 9

= lim

x −

(x −1)(x − 2)( x

+ 7 + 3)

(x −1)(x − 2)(

x + 7 + 3)

x→2

= lim

(x −1)(

x + 7 + 3)

x→2

Пример 3.5. Вычислить lim

sin 7x

x→0

tg3x

Решение. Для раскрытия неопределенности

воспользуемся пер-

вым замечательным пределом. Считая, что

x ≠ 0 , проведем очевид-

ные преобразования:

sin 7x

lim

= lim

lim

cos 3x =

sin 3x

x→0 tg3x

x→0

cos 3x 3x

lim

sin 7x

x→0

lim cos 3x =

1 =

3 lim sin 3x

x→0

Пример 3.6. Вычислить

lim

−

x → ∞

Решение. Для раскрытия неопределенности 1∞

воспользуемся вто-

рым замечательным пределом:

−

−2

= e

−2

lim 1

−

= lim

−

x→∞

−

поскольку lim 1

−

lim 1 +

= e .

x→∞

y=−

→∞

§ 5. Сравнение бесконечно малых функций

Для сравнения двух бесконечно малых функций α(x) и β(x) в

точке x = a находят предел отношения lim α(x) = A .

x→a β(x)

Если A ≠ 0 и A ≠ ∞ , то функции α(x) и β(x) называются

бесконечно малыми одного порядка.

Если A = 0 , то α(x) называется бесконечно малой высшего порядка по сравнению сβ(x) . Записывается это так: α(x) = o(β(x)) .

Если A=1, то бесконечно малые функции α(x) и β(x) называют эквивалентным и обозначают α(x) ~ β(x) . Например, sin x ~ x при

x → 0 , так как lim	sin x	=1.

x→0	x
Основные эквивалентности при x → 0 :
	sin kx ~ kx ,		tgkx ~ kx ,
	arcsin kx ~ kx ,		arctgkx ~ kx ,
	ln(1 + kx) ~ kx ,		ekx -1 ~ kx .

При вычислении пределов используют следующую теорему.

Теорема. Предел отношения двух бесконечно малых функций в некоторой точке равен пределу отношения эквивалентных им бесконечно малых функций в той же точке.

Доказательство см. [1], гл. II, §11.

Пример 3.7. Вычислить lim	1 − cos 5x	.
x→0	x sin 3x

Решение. Воспользуемся эквивалентными бесконечно малыми функциями. Так как при x → 0

1 − cos 5x =

2 5x

5x 2

= 25

и sin 3x ~ 3x , то

2sin

~ 2

1 − cos 5x

lim

= lim

x sin 3x

x→0

x 3x

§ 6. Непрерывность функции

Определение. Функция y = f (x)

называется непрерывной в точ-

ке

x = x0 ,

если

предел

функции

точке

x0 существует и

lim f (x) = f (x0 ) .

x→x0

Односторонними называются пределы:

lim f (x) =

lim

f (x) = f (a − 0)

- левосторонний предел в точке a ;

x→a

x→a−0

x<a

lim f (x) = lim

f (x) = f (a + 0) - правосторонний предел в точке a .

x→a

x→a+0

x>a

Определение. Функция y = f (x) называется непрерывной в точке x = x0 , если существуют односторонние пределы в точке x0 и

lim	f (x) = lim f (x) = f (x0 ) .	(*)
x→x0 −0	x→x0 +0

Если односторонние пределы конечны, но нарушается хотя бы одно из равенств (*), то x0 называется точкой разрыва 1-го рода.

Если хотя бы один из этих односторонних пределов не существует или равен бесконечности, то x0 называется точкой разрыва второго рода.

Например, функция

y =

x −1

1, если x > 1,

имеет в точке

−1, если x <

x −1

x =1 разрыв 1-го рода (рис. 3.2).

-1

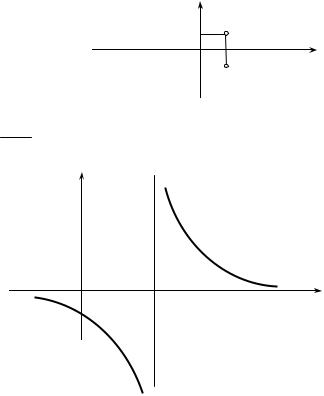
Рис. 3.2

Функция y = x −1 2 имеет в точке x = 2 разрыв второго рода

(рис.3.3).

Рис.3.3

Если функция непрерывна во всех точках отрезка [a,b], то она

называется непрерывной на этом отрезке.

Из определения непрерывности функции и теорем о пределах следуют теоремы:

I. Если функции f (x) и g(x) непрерывны в точке x0 , то в этой

точке		непрерывны	функции	f (x) + g(x) ,	f (x) g(x) ,
	f (x)	(g(x0 ) ≠ 0) .
	g(x)	(g(x0 ) ≠ 0) .
	g(x)

II. Сложная функция, составленная из непрерывных функций, непрерывна в соответствующей точке.

III. Всякая элементарная функция непрерывна в каждой точке своей области определения.

Доказательство приведено, например, в [1], гл. 2, §9.

ЗАДАЧИ ДЛЯ УПРАВЛЯЕМОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ

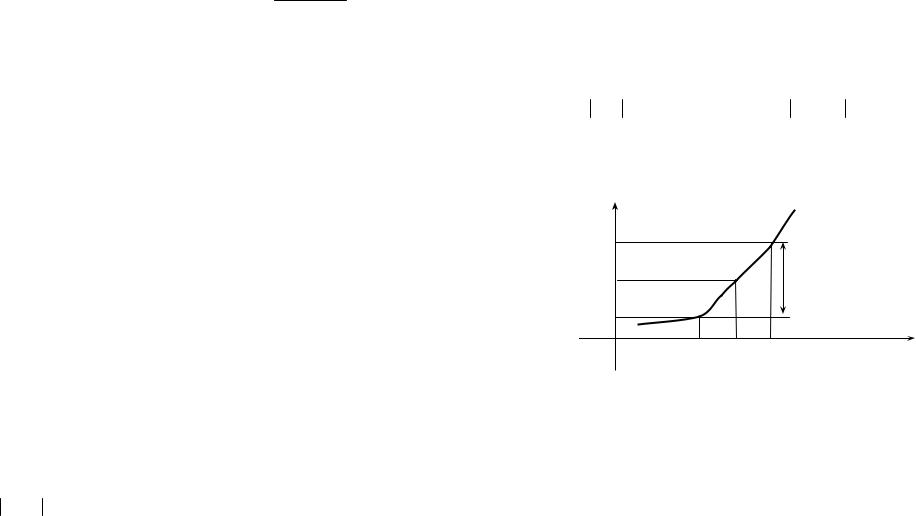
1.Найти область определения функции y = 9 − x2 .

2.Найти указанные пределы

а)

lim

x2 −1

;

б)

lim

−

;

5x2

(x − 2)2

x→1

− 4x −1

x→2

в)

lim

5 −

2x − 3x

;

г)

lim

−

3x + 4

;

+ x +

3 + 5x −1

x→∞

x→∞ 2x

д)

lim

2x + 3 −

;

е)

lim

sin

2 2x

;

x2 − 9

x→3

x→0

ж) lim

sin 4x

з)

+ 3 x

;

lim

tgx

x→0

x→∞

КОНТРОЛЬНЫЙ ТЕСТ ПО МОДУЛЮ №3


10. Пусть f (x)=	x +1	. Тогда D(f )=
	x2 −1
а) (− ∞; + ∞);		б) (1; + ∞);

в) (− ∞; −1) (1; + ∞);		г) (− ∞; −1) (−1;1) (1; + ∞).

20. Какие из данных функций являются четными?
а) y = cos 2x ;	б) y = ctg3x ;		в) y = 2tg3x ;	г) y = −3sin x .

30. Какая из функций не является сложной функцией?

а) y = 2x2

;

б) y = log30 x ;

в) y = sin(x2 );

г) y = cos(2x).

4. В указанном множестве функций найдите бесконечно малые

при x → 0 функции:

а) y = 2x + 3 ;

б) y = 2x−1 ;

в) y = cos 2x ;

г) y = x + 4 − 2 .

5. Найти предел lim

sin αx

x→0 sin βx

а) e ;

б) ∞ ;

в)

;

г) α .

6. lim

равен

x −1

x→1

а)1;

б)-1;

в)

∞ ;

г) не существует.

7*. Функция sin 2 3x при x → 0 эквивалентна функции

а) 3x ;

б) 3x2 ;

в) 9x2 ;

г) 6x .

8*. Известно, что lim f (x)= −∞ ,

lim f (x)=18 . Какое из

x→c−0

x→c+0

утверждений верно?

а) c - точка неустранимого разрыва первого рода; б) c - точка устранимого разрыва первого рода; в) c - точка разрыва второго рода;

г) c - точка непрерывности.

Модуль 4.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

§1. Производная функции, ее геометрический

имеханический смысл


Пусть функция y = f (x)			определена в некоторой окрестности
точки х. Если переменная х получит приращение								x , то функция у
получит приращение	y = f (x +			x) − f (x) .
Определение. Производной функции y = f (x)								в точке х называ-
ется предел отношения приращения функции								y к приращению
аргумента x , когда	x →0 , т.е.
y′ = lim		y	= lim			f (x +	x) − f (x)		.
		x
	x→0		x→0				x
Для производной функции			y = f (x) в точке х применяют также
	′		dy		df (x)
обозначения:	f (x) = dx			=		dx	.

Функция, имеющая в данной точке конечную производную, называется дифференцируемой в этой точке.

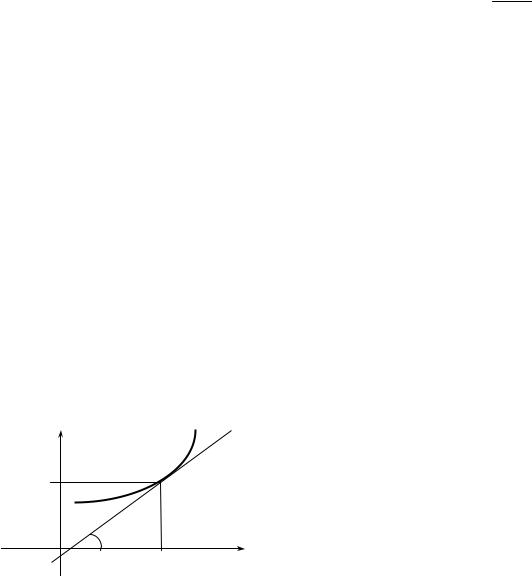
Геометрический смысл производной. Построим график функ-

ции y = f (x) и проведем к нему касательную через точку M (x0 , f (x0 )) (рис.4.1). Обозначим через α угол, образованный этой касательной c осью Ox , тогда tgα = f ′(x0 ) ,

т.е. производная f ′(x0 ) функции y = f (x) равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x0 .

y = f (x)

Рис.4.1 f (x0)

	α
0	x0	x

Уравнение	касательной к кривой y = f (x)	в точке
M (x0 , f (x0 ))	имеет вид y − f (x0 ) = f ′(x0 )(x − x0 ) ,	а уравнение

нормали к данной кривой в этой же точке записывается в виде y − f (x0 ) = − f ′(1x0 ) (x − x0 ) при условии, что f ′(x0 ) ≠ 0 .

Если f ′( x0 ) = 0 , то уравнение касательной: y = f (x0 ) , а уравнение

нормали: x = x0 .

Механический смысл производной. Пусть материальная точка движется прямолинейно по закону s = s(t) . Тогда v = s′(t) , т.е.

производная от пути по времени есть скорость движения точки.

§ 2. Основные правила дифференцирования

Если функции u и v дифференцируемы, то

1.(cu)′ = cu′, c = const .

2.(u ± v)′ = u′± v′ .

3.(u v)′ = u′ v + u v′.

4.	u	′	u′ v − u v′	,	v ≠ 0 .
4.		=		,	v ≠ 0 .
	v		v2

5.Если y = f (u) и u = ϕ(x) - дифференцируемые функции своих аргументов, то сложная функция y = f (ϕ(x)) тоже дифференци-

руема и y′x = yu′ u′x

или

Это правило легко распространить на цепочку из любого конеч-

ного числа дифференцируемых функций.

Если для дифференцируемой функции y =

f (x)

′

( f (x) ≠ 0) суще-

ствует обратная функция x = ϕ( y) , то ϕ′

или

x′ =

(y)

′

f (x)

Если функция задана параметрическими уравнениями

x = x(t),

то ее производная вычисляется по формуле

y = y(t),

yt′

y′(x) =

y′(t)

или

y′ =

x′(t)

xt′

§3. Таблица производных основных элементарных функций

Вприводимой ниже таблице: c = const ; α R ; a > 0 , a ≠1; u = u(x) .

Производные основных

Производные сложных функ-

элементарных функций

ций

c′ = 0 ; x′ =1;

(xα )′ = αxα−1 ;

(u α )′ = αu α−1u′ ;

( x )′ = 1 ;

( u )′ = 1 u′;

(a x )′ = a x ln a ;

(au )′ = au ln au′ ;

(e x )′ = e x ;

(eu )′ = eu u′;

(loga x)′ =

;

(loga

u)′ =

u′

;

u ln a

x ln a

′

(ln x)

;

(ln u)

u′;

(sin x)′ = cos x ;

(sin u)′ = cosu u′;

(cos x)′ = −sin x ;

(cos u)′ = −sin u u′;

′

(tgx)

;

(tgu)

u′;

cos2 u

cos2 x

(ctgx)′ = −

;

(ctgu)′ = −

u′

sin 2

(arcsin x)′ =

;

(arcsin u)′

u′ ;

1 − x2

1 − u 2

(arccos x)′ = −

;

(arccos u)′ = −

u′;

1 − x2

1 − u 2

′

(arctgx)

;

(arctgu)

u′;

1 + x2

1 + u 2

′

(arcctgx)

= −

;

(arcctgu)

= −

u′.

1+ x 2

1+u 2

Доказательство справедливости указанных формул смотрите в

[1], гл.3, §5, 6, 8, 10, 12, 14.

Пример 4.1. Найти производную функции y = 2x4 − 43 x2 + x25 .

Решение. Данную функцию представляем в ви-

	4		2		−5				′					2		′		′
																	−5
			3					4													3
													3
де y =2x		−4x		+2x		.	y′ = 2(x		)				3			+ 2(x		)	= 2 4 x			−
де y =2x		−4x		+2x		.	y′ = 2(x		)	− 4 x						+ 2(x		)	= 2 4 x			−

											2	x−	1		+ 2 (−5)x−6 =8x3 −					8			1 −	10 .
								− 4			2		3							8
								− 4			3		3							3
											3									3			3 x	x6

Пример 4.2. Найти производную функции y = tg 3 7x .

Решение. Последовательно используем формулы для производных сложных функций

)

′

= 3u

′

y′ = (tg 3 7x)′ =

u ,

= 3tg 2 7x(tg7x)′

(tgu)′ = cos2 u

u′,

гдеu = tg7x

гдеu = 7x

′

sin 2 7x

= 3tg

7x cos2 7x

(7x)

= 3tg

7x cos2 7x 7 = 21 cos4 7x .

Здесь при решении указывались формулы, которые применялись при вычислении производных.

Пример 4.3. Найти производную функции y = ln arctg x .

Решние.

y′ = (ln arctg x)′ =

(ln u)

′

(arctg x )′ =

= u u , =

гдеu = arctg x

arctg

= (arctgu)′ =

u′, =

(

x )′ =

1 + u 2

x )2

где

u =

arctg

1 + (

1 .

arctg

1 + x

Пример 4.4. Найти производную функции y = (x −1)2 x2 + 3x −1 .

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.20161.26 Mб80Магнетизм. Лабораторный практикум.pdf
#
13.09.201983.46 Кб8Макр. Нестаб. (2).doc
#
13.09.2019303.62 Кб5Макроэк. равновесие в класс.мод.. 2.doc
#
22.02.2016521.22 Кб20Макроэк.равн. IS-LM.doc
#
22.02.2016828.42 Кб63МАРКЕТИНГ.doc
#
22.02.20161.03 Mб20Математика. Часть 1.pdf
#
22.02.20163.92 Mб121Материаловедение_лабараторный практикум.pdf
#
22.02.20163.92 Mб56Материаловедение_лабпракт.pdf
#
22.02.2016959.49 Кб67Материалы - Менеджмент (ТОМ) - 17-24зэи.doc
#
22.02.2016334.34 Кб35Материалы к ГЭК 2012.doc
#
22.08.2019272.9 Кб6материалы по преддипл. практике рем 2012 год..doc