68
.pdf
52. Электростатическое поле на границе двух диэлектриков. Вывод граничных условий для тангенциальных и нормальных составляющих векторов напряженности электрического поля (E) и вектора электрического смещения (D) на границе раздела двух диэлектриков. Закон преломления линий напряженности электростатического поля и линий электрического смещения на границе раздела диэлектриков.
53. Равновесное распределение зарядов в проводнике. Электростатическое поле внутри проводника. Необходимые условия равновесного распределения зарядов в проводнике. Электростатическая защита.
Электростатическая защита.При внесении незаряженного проводника в электрическое поле происходит разделение зарядов, свободные заряды образуют на одной стороне избыток отрицательных зарядов, а на другой – избыток положительных зарядов (рис. 19.2).
Это явление называется электростатической индукцией, а заряды – индуцированными зарядами. При равновесном состоянии поле внутри проводника равно нулю. Линии напряженности вне проводника перпендикулярны к его поверхности. Нейтральный проводник, внесенный в электрическое поле, разрывает часть линий напряженности – они начинаются на положительных и заканчиваются на отрицательных индуцированных зарядах. Внутри поле отсутствует.
На свойстве проводников экранировать внешние поля основывается электростатическая защита от действия внешних электростатических полей. Когда какой – либо прибор хотят защитить от воздействия внешних полей, его окружают проводниковым экраном. Внешнее поле компенсируется внутри экрана возникающего на его поверхности электрическими зарядами. При этом экран может быть не сплошным, а в виде густой сетки. Заметим, что если заряды
находятся внутри полости, то они вызывают возникновение индукционных зарядов и на внутренней и на внешней поверхности проводника. Поле внутри полости в этом случае отлично от нуля.
Свободные электрические заряды в проводнике могут перемещаться под действием сколь угодно малой силы. Поэтому равновесие зарядов в проводнике может наблюдаться только при выполнении следующих условий:
1.Напряженность электрического поля внутри проводника должна быть равна нулю, т.е. = 0. то потенциал внутри проводника остается постоянным.
2.Напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности. Следовательно, в случае равнове¬сия зарядов, поверхность проводника является эквипотенциальной поверхно¬стью
Если бы эти условия не выполнялись, то на свободные заряды, имеющиеся в каждом проводнике, действовала сила, и равновесие было бы нарушено.
[продолжение 53]
Земля также является проводником, и заряды на ней находятся в равнове¬сии. Поэтому можно считать, что всё точки земли имеют одинаковый потенци¬ал. По этой причине постоянную точку при измерении потенциала часто выби¬рают на поверхности земли и говорят о потенциале относительно земли.
Так как при равновесии зарядов на проводнике напряженность поля в нем равна нулю, то поток вектора напряженности через любую замкнутую поверх¬ность, проведенную внутри проводника, равен нулю. Из теоремы Гаусса 1.9 следует, что в этом случае поверхность электрических зарядов не охватывает. Следовательно, при равновесии, внутри проводника не может быть электриче¬ских зарядов. Все они расположатся на поверхности проводника с некоторой поверхностной плотностью о. Заряды в состоянии равновесия распределяются по поверхности проводника всегда, независимо от того каким образом возни¬кают эти заряды.
Так как в состоянии равновесия зарядов внутри проводника нет, то удале¬ние вещества из некоторого объема, взятого внутри проводника, никак не от¬ражается на распределении зарядов. Это озна¬чает, что избыточный заряд распределяется на полом проводнике так же, как и на сплошном, т.е. на его наружной поверхности. На поверх¬ности полости заряды располагаться не могут. Это явление широко используется в электро¬статической защите и генераторе Ван-де-Граафа.
Электростатическое поле внутри проводника.Наличие в проводнике свободных зарядов приводит к тому, что внутри проводника электростатическое поле равно нулю. Если бы напряженность электрического поля была отлична от нуля, то поле приводило бы свободные заряды в упорядоченное движение, т.е. в проводнике существовал бы электрический ток. Утверждение об отсутствии электростатического поля внутри проводника в равной мере справедливо как для заряженного проводника, так и для незаряженного, помещенного во внешнее электростатическое поле. (Конечно, отдельные заряженные частицы - электроны и ионы - создают микроскопические поля. Но эти поля взаимно компенсируют друг друга, и среднее значение напряженности их поля оказывается равным нулю.)
54. Связь векторов напряженности электростатического поля (Е) и электрического смещения (D ) вблизи поверхности проводника с
поверхностной плотностью свободных зарядов на проводнике (вывод соответствующих формул для случаев проводник-вакуум и проводникдиэлектрик). Зависимость распределения заряда по поверхности проводника от его геометрии. Явление истечения заряда с острия.
56. Общая задача электростатики. Уравнение Пуассона; уравнение Лапласа. Теорема единственности.
Общей задачей расчета электростатического поля является определение напряженности поля во всех его точках по заданным зарядам или потенциалам тел. Для электростатического поля задача полностью решается отысканием потенциала как функции координат. Обратная задача отыскания распределения зарядов по заданному распределению зарядов решается с помощь уравнения Пуассона или с помощь уравнения Лапласа и граничного условия у поверхности заряженных проводящих тел. Это наиболее простой тип задач.
Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое описывает
•электростатическое поле,
•стационарное поле температуры,
•поле давления,
•поле потенциала скорости в гидродинамике.
Это уравнение имеет вид: 
где 
— оператор Лапласа или лапласиан, а 
— вещественная или комплексная функция на некотором многообразии.
В трёхмерной декартовой системе координат уравнение принимает форму:
Уравнение Лапласа — дифференциальное уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так:
и является частным случаем уравнения Гельмгольца.
Ситуация однако становится однозначной, если мы, например, зададим потенциалы всех проводников (и, разумеется, величины всех точечных зарядов, если помимо зарядов на проводниках имеются еще точечные заряды в пространстве вокруг них) и выберем начало отсчета потенциала так, чтобы на бесконечности ∆ᵠ=∞ тогда решение будет так
ᵠ1 ᵠ2 ᵠ3 ᵠ=0
Лапласа, дополненное такими граничными условиями для функциистановится вполне однозначным или, как говорят, единственным.
57. Электроемкость. Электроемкость уединенного проводника. Электроемкость шара. Взаимная электроемкость двух проводников. Конденсаторы. Электроемкость плоского конденсатора. Вывод формулы для расчета электроемкости батареи конденсаторов, соединенных параллельно. Предельное допустимое напряжение при параллельном соединении конденсаторов.
Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.
Электроемкость уединенного проводника — физическая величина, равная отношению электрического заряда уединенного проводника к его потенциалу
C=qφ
. В СИ единицей электроемкости является фарад (Ф).Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):
Взаимная электроемкость двух проводников численно равна заряду, который нужно перенести с одного проводника на другой для изменения разности потенциалов между ними на единицу.
Электрическая емкость уединенного проводника зависит от его формы и размеров, а также от величины относительной диэлектрической проницаемости среды, в которой он находится. Электроемкость не зависит от материала проводника, его агрегатного состояния, от формы и размеров возможных полостей внутри проводника. Электроемкость не зависит также ни от заряда проводника, ни от его потенциала.
В качестве примера найдем электроемкость уединенного проводящего шара радиуса R, покрытого слоем диэлектрика с относительной проницаемостью 
и толщиной d. Пусть шар имеет заряд q. Тогда напряженность поля, создаваемого шаром внутри диэлектрического слоя,
Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом.
Напряженность 
поля между двумя пластинами плоского конденсатора равна сумме напряженностей полей, создаваемых каждой из пластин:
Если на пластинах площадью S находятся электрические заряды +q и -д, то на основании формул (17.5) и (17.6) для модуля напряженности поля между пластинами можем записать
Напряжение в любых случаях не может превысить величины ЭДС источника тока.
59. Энергия электростатического поля. Объемная плотность энергии электростатического поля. Энергия взаимодействия неподвижных точечных зарядов. Энергия уединенного проводника и энергия заряженного конденсатора.
В пределах электростатики невозможно дать ответ на вопрос, где
сосредоточена энергия конденсатора. Поля и заряды, их образовавшие, не могут существовать обособленно. Их не разделить. Однако переменные поля могут существовать независимо от возбуждавших их зарядов (излучение солнца, радиоволны, …), и они переносят энергию. Эти факты заставляют признать, что носителем энергии является электростатическое поле.
При перемещении электрических зарядов силы кулоновского взаимодействия совершают определенную работу dА. Работа, совершенная системой, определяется убылью энергии взаимодействия -dW зарядов
. |
(5.5.1) |
Энергия взаимодействия двух точечных зарядов q1 и q2, находящихся на расстоянии r12, численно равна работе по перемещению заряда q1 в поле
неподвижного заряда q2 из точки с потенциалом 
в точку с потенциалом 
:
Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему. Для однородного поля
объемная плотность энергии равна 
. Для плоского конденсатора, объем которого Sd, где S - площадь пластин, d - расстояние между пластинами, имеем
С учетом, что и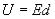 
Энергия системы неподвижных точечных зарядов. Электростатические силы взаимодействия консервативны (см. § 83); следовательно, система зарядов обладает потенциальной энергией. Найдем потенциальную энергию системы двух неподвижных точечных зарядов Q1 и Q2, находящихся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией
(см. (84.2) и (84.5)):
где ϕ12 и ϕ21 — соответственно потенциалы, создаваемые зарядом Q2 в точке нахождения заряда Q1 и зарядом Q1 в точке нахождения заряда Q2. Согласно (84.5),