
Metod_2a_2002
.pdf
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
(МУ) |
|
|
|
|
Нормальные |
|
|
напряжения |
в |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
(МХ) |
|
произвольной |
точке А(х,у) сечения |
|||||||||||||||||
Растянутая зона |
|
МУ |
|
|
можно найти по формуле |
|
|
|
|
|
|||||||||||||
|
(N) |
|
|
|
P |
|
MyxA |
|
M |
|
y |
|
|
|
|
|
|
|
|||||
|
Р |
|
у |
|
|
|
x |
A |
|
(5.4) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||
|
У |
А |
|
|
|
A |
|
|
|
Iy |
|
|
|
Ix |
|
|
|
|
|
|
|
||
ХN |
МХ |
X |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
Учитывая соотношения |
|
|
|
|
|
|
|
||||||||||||||
|
х |
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
Iy |
|
|
|
|
|
|
|
|
УN |
|
|
|
|
|
ix |
x , |
|
|
iy |
|
|
|
, |
|
(5.5) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
определяющие |
|
значения |
|
главных |
||||||||||||||
|
Нейтральная |
|
|
|
радиусов инерции сечения, получим |
|
|
||||||||||||||||
|
|
|
|
|
|
P |
|
|
xp |
xA |
|
|
yp yA |
|
|
|
|
||||||
|
линия |
|
|
|
у |
|
|
|
(5.4) |
I |
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
A |
F |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iy |
|
|
|
|
|
|
ix |
|
|
|
|
||
|
В |
отличие |
от сложного |
Рис. 5.3 |
(косого) |
изгиба при |
внецентренном |
сжатии нейтральная линия не проходит через центр тяжести сечения. Положение этой линии, из условия равенства нулю нормальных напряжений , определим отрезками, которые она отсекает на главных осях инерции:
xN |
|
i2y |
, yN |
|
i2 |
|
|
|
x |
(5.6) |
|||||
xp |
yp |
||||||
|
|
|
|
|
Нейтральная линия делит площадь сечения на две части, в которых нормальные напряжения имеют противоположные знаки. Положение нейтральной линии зависит от координат точки В, где приложена сила Р. Наибольшие по абсолютной величине нормальные напряжения возникают в наиболее удаленных точках в сжатой и растянутой зонах сечения. Для определения положения этих точек достаточно провести касательные к контуру сечения, параллельные нейтральной линии. Точки касания и будут являться точками с наибольшими по модулю нормальными напряжениями. Важно отметить следующие положения: если точка приложения силы лежит на одной из главных осей инерции и перемещается вдоль нее, то нейтральная линия также перемещается, оставаясь параллельной другой главной оси инерции. Справедливо и обратное утверждение: если нейтральная линия перемещается, оставаясь параллельной одной из главных осей инерции, то точка приложения В силы Р перемещается вдоль другой главной оси инерции (рис.5.4). Следует заметить, что если сила из бесконечности приближается к центру тяжести сечения, нейтральная линия удаляется неограниченно.

|
|
|
|
|
24 |
2' |
1' |
y |
|
|
Нейтральная |
|
|
линия (сила в |
|||
|
|
|
|
|
|
|
|
|
|
|
точке С) |
|
|
0 |
B2 |
B1 |
X |
|
|
ц.т. |
|
(P) |
|
|
|
|
|
|
|
|
|
|
|
|
Нейтральные |
|
|
|
|
|
линии |
a)
y |
|
|
A |
|
|
|
(P) |
|
|
B |
|
0 |
C |
X |
ц.т. |
|
|
D |
|
|
|
|
Нейтральная |
б) |
|
линия (сила в |
|
точке А) |
Из рис. 5.4б следует, что точка приложения В силы Р смещается вдоль прямой АС общего положения (из точки В в точку С), нейтральная линия поворачивается вокруг некоторой точки D. Справедливо и обратное утверждение: если нейтральную линию поворачивать вокруг точки D, то точка приложения силы будет перемещаться вдоль прямой АС общего положения. Обратные утверждения широко используются при построении некоторой воображаемой области, расположенной вокруг центра тяжести. Эта область обладает замечательным свойством: в какой бы точке этой области ни находилась сила Р, во всех точках поперечного сечения нормальные напряжения имеют один знак. Эту область принято называть ядром сечения.
Очевидно, что если сила будет находится на контуре ядра сечения, нейтральная линия будет касаться контура поперечного сечения. Отсюда вытекает правило построения ядра сечения. Задаемся серией нейтральных линий, касательных к контуру поперечного сечения, определяем для каждой из них отрезки, отсекаемые на главных осях инерции х, у ах и ау соответственно (с учетом знаков), и по формулам
xя |
|
i2y |
, yя |
|
i |
2 |
, |
|
|
|
x |
(5.7) |
|||||
ax |
|
|
||||||
|
|
|
|
ay |
|
|||
найдем координаты точек, принадлежащих контуру ядра сечения. Величины отрезков ах и ау для сечения ломаного очертания можно найти из уравнения прямой, проходящей через две точки:
x x1 |
|
y y1 |
(5.8) |
|
x2 x1 |
y2 y1 |
|||
|
|
где x1, y1 и x2, y2 координаты точек контура сечения, через которые проходит заданная нейтральная линия;
x, y текущие координаты точек нейтральной линии. Если принять y = 0, x = ах, то
|
|
ax |
x1 |
|
x2 x1 y1 |
. |
(5.9) |
|
|
|
|
||||||
А если принять x = 0, y = ау, то |
|
|
|
|
y2 y1 |
|
||
|
|
y2 y1 x1 . |
|
|||||
a |
y |
y |
|
(5.10) |
||||
|
1 |
|
x2 x1 |
|
||||
|
|
|
|
|
|
|||
Если очертание контура сечения криволинейное, то необходимо написать уравнение линии этого контура. Затем записать уравнение касательной к этой линии и определить
25
соответствующие отрезки, отсекаемые нейтральной линией на главных осях инерции. В работе это не используется, поэтому такие соотношения здесь не приводятся.
5.3.Порядок выполнения работ
5.3.1.Порядок расчета балки на сложный (косой) изгиб:
а) Строим эпюры поперечных сил и изгибающих моментов в горизонтальной и вертикальной плоскостях и определяем положение опасного сечения; б) Устанавливаем сечение балки рационально относительно главных центральных осей инерции;
в) Из условия прочности назначаем размеры сечения балки; г) Определяем положение нейтральной линии;
д) Находим нормальные напряжения в угловых точках сечения балки; е) Строим эпюру напряжений в аксонометрии.
5.3.2. Порядок расчета короткой стойки на внецентренное сжатие:
а) Выполняем разбивку сечения стойки на элементарные площади и определяем координату центра тяжести; б) Вычисляем осевые моменты и квадраты радиусов инерции
центральных осей x, y, соответственно;
в) Определяем положение нейтральной линии отрезками xN и yN, которые она отсекает на главных центральных осях; находим положение опасных точек в растянутой и сжатой зонах сечения; г) Находим размеры поперечного сечения стойки из условия прочности материала на
растяжение и сжатие; назначаем необходимые размеры; д) Вычисляем нормальные напряжения во всех угловых точках сечения и строим аксонометрическую эпюру напряжений; е) Строим ядро сечения стойки.
5.4.Содержание расчетных работ
5.4.1.Содержание задачи на косой изгиб.
Для стальной балки прямоугольного поперечного сечения необходимо:
построить эпюры поперечных сил Qx, Qy и изгибающих моментов Мх и Му в аксонометрии и определить положение опасного сечения;
рационально расположить поперечное сечение балки;
определить безопасные размеры поперечного сечения b и h при соотношении k = h/b;
указать положение силовой и нейтральной линий;
вычислить величину нормальных напряжений i в угловых точках поперечного сечения балки и построить эпюру этих напряжений в аксонометрии.
Врасчете принять расчетное сопротивление стали R = 210 МПа.
Данные взять из таблицы 5.2.
Пример расчета балки на сложный изгиб
Рассмотрим стальную балку прямоугольного поперечного сечения (рис.5.5а), защемленную с одной стороны, нагруженную силой Р = 20 кН под углом р= 450 и равномерно распределенной нагрузкой q = 12кН/м в вертикальной плоскости yoz и сосредоточенной парой сил с моментом М = 8 кН·м в горизонтальной плоскости xoz.
Соотношение k = h/b=1,6. |
26 |
Расчетное сопротивление R = 210 МПа. Силу Р = 20 кН |
|
разложим на составляющие |
Px = Pcos450 = 14,14 кН, Ру= Psin450 = 20 · 0,707 = 14,14 |
кН. |
|
1)Построение эпюр изгибающих моментов выполним независимо в горизонтальной
ивертикальной плоскостях.
а) Горизонтальная плоскость xoz. |
|
|
|
|
||
Участок I. Qx (z) = 0, |
My(z) = 0, 0 z 1 м. |
|
|
|||
Участок II. Qx (z) = 14,14 кН= const, |
|
|
|
|
||
My(z) =Pxz, 0 z 1 м, |
|
|
|
|
||
My(0)=0, Му (1) = 14,14· 1 = 14,14 кН·м. |
|
|
||||
Участок III. Qx (z) = 14,14 кН = const, |
My(z) = Px(1+z) + М, 0 z 1,4м, |
|||||
Му(0) = 14,14(1+0) + 8 = 22,14 кН·м, |
|
Му(1,4) =14,14(1+1,4) + 8 =41,94 кН·м |
||||
б) Вертикальная плоскость yox. |
|
|
|
|
||
Участок I. Qy(z) = qz, 0 z 1 м. |
|
|
|
|
||
Qy(0) = 0, Qy(0) = 12 кН, |
|
Mx (z) q |
z2 |
|||
|
2 |
|
||||
|
|
12 12 |
|
|
|
|
Mx(0) = 0, |
Mx (1) |
6 кН·м. |
|
|
||
|
|
|
||||
|
2 |
|
|
|
|
|
Участок II. Qy(z) = 12 + 14,14 = 26,14кН = const Mx(z) = q·1·(0,5+z) + Pуz, 0 z 1 м, Мх(0) = 6 кН·м,
Мх(1) = 12·1(0,5+1) + 14,14 · 1 = 32,14 кН·м.
Участок III. Qy(z) = 26,14кН = const,
Mx(z) = q·1·(1,5+z) + Py(1+z), 0 z 1,4 м, Mx(o) = 32,14 кН·м
Mx(1,4) = 12 · 2,9+ 14,14 · 2,4 = 68,74 кН·м.

27
По этим результатам счета строим эпюры изгибающих моментов МУ и МХ (рис.5.5
а,б, в, г, д).
 q=12кН/м Py
q=12кН/м Py
P 

z
M=8 |
кНм |
|
 Px
Px
|
|
) |
Эпюра |
Qx |
(кН |
|
||
|
|
|
|
) |
Эпюра |
My |
(кНм |
|
||
|
|
|
|
|
|
|
|
|
) |
|||
Эпюра |
Qy |
(кН |
||||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
кНм |
Мх |
( |
Эпюра
Рис. 5.5
2) Определение положения опасного сечения балки выполним по максимальному результирующему моменту
MИЗГ M2x M2y 
 68,742 41,942 80,52 кН·м
68,742 41,942 80,52 кН·м

28
Других сечений, где бы Мизг был больше чем 80,52 кН·м, нет. Следовательно, сечение балки вблизи заделки является опасным.
3)Рациональное расположение сечения диктуется величиной изгибающего момента Мх =68,74 кН·м, который больше чем Му = 41,94 кН·м в том же опасном сечении. Поэтому балку прямоугольного сечения ставим так, чтобы момент сопротивления Wx был больше Wy, а это означает, что больший размер сечения балки нужно поставить вертикально.
4)Подбор сечения балки выполним по формуле 5.3:
|
|
у |
|
|
|
|
|
|
M |
x |
|
|
My |
|
R, или у |
|
|
|
6 |
|
M |
x |
|
|
|
6 |
My |
R, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
РАСЧ |
|
|
|
|
|
|
РАСЧ |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
W |
W |
bh2 |
|
|
hb2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но так как h/b = k, то h= kb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
Mx |
|
|
|
My |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6 |
|
|
|
|
|
|
|
6 103 |
68,74 |
|
|
|
41,94 |
|
|
2 |
|
||||||||||||||||||||
b 3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
11,83см |
||||||||||
|
|
|
k2 |
k |
|
|
|
2 10 106 |
1,6 |
|
1,6 |
|
|
||||||||||||||||||||||||
|
|
R |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Принимая b = 12 см, найдем: h = kb = 1,6 · 12 = 19,2 см.
 y
y
4 |
1 |
 Силовая линия
Силовая линия
Размеры |
балки |
назначаем |
окончательно: |
|
|
b = 12 см, h = 19 см |
(рис.5.6). |
|
5) Определение положения нейтральной линии:
h = 19 см
Зона сжатия
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
My |
|
I |
z |
41,94 |
192 |
1,5295 |
|
tgв |
|
|
122 |
|||
x |
Mx |
|
Iy |
68,74 |
|
||
= arctg (-1,5296) = 56049 . |
|
||||||
6) Положение силовой линии определим из отношения (это след плоскости действия результирующего  момента):
момента):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
My |
|
41,94 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
ctgб |
|
|
|
|
|
0,6101 |
||||
|
|
|
|
|
Рис. 5.6 |
|
|
|
|
Mx |
68,74 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= arcctg(0,6101) = 58037 . |
|||||||||||
|
Положение силовой и нулевой линий в опасном сечении балки показано на рис.5.6. |
|||||||||||||||||||||||
|
7) Вычисление нормальных напряжений в угловых точках (1, 2, 3, 4) поперечного |
|||||||||||||||||||||||
сечения балки и построение эпюры нормальных напряжений в аксонометрии. |
||||||||||||||||||||||||
|
Воспользуемся формулой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
у |
|
|
Mx y(i) |
|
|
Myx(i) |
|
12Mx y(i) |
|
12Myx(i) |
|
, |
|
||||||
|
|
|
|
|
|
(i) |
|
|
Ix |
|
Iy |
bh3 |
|
hb3 |
|
|
|
|
||||||
|
у(1) |
12 68,74 103 |
9,5 10 2 |
|
|
12 41,94 6 103 10 2 |
95,2 91,97 МПа |
|||||||||||||||||
|
|
|
|
|
|
|
|
19 123 10 8 106 |
||||||||||||||||
|
|
|
|
|
12 193 10 8 106 |
|
|
|
|
|
|
|
||||||||||||
|
(1) |
= 95,2 + 91,97 = 187,17 МПа, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
(2) |
= 95,20 + 91,97 = 3,23 МПа, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
(3) |
= -95,20 – 91,27 = -187,17 МПа |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
(4) |
= 95,20 – 91,97 = -3,23 МПа |
|
|
|
|
|
|
|
|
|
|||||||||||||
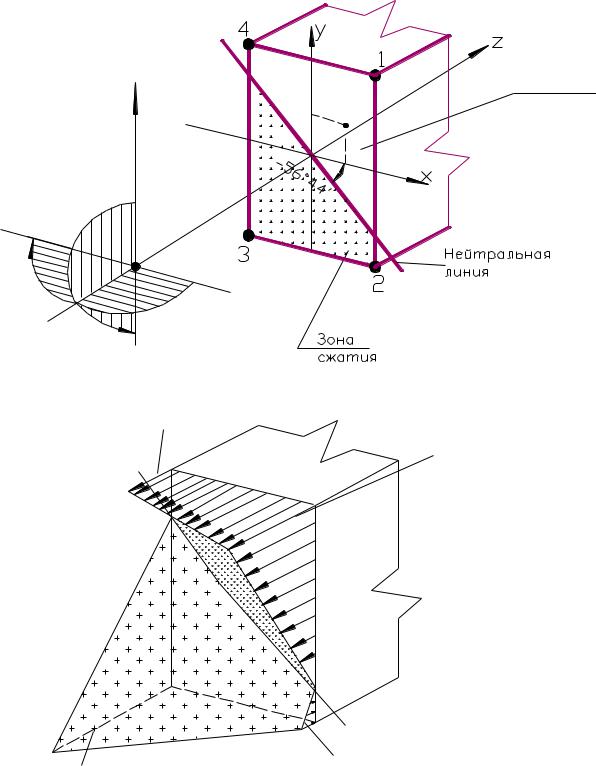
29
a)
(IV)
Mx=41.94кНм
(x)
Mx=68.74кНм
Зона
растяжения
(i)



 yi
yi 



 xi
xi
(4)=3.23 МПа
(1)=187.2 МПа
б)
(2)=3.23 МПа
(3)=187.2 МПа
Рис. 5.7
На рис.5.7а показаны направления изгибающих моментов Му и Мz и направления нормальных напряжений в точке, расположенной в первой четверти главных центральных осей инерции сечения балки. На рис.5.7б представлена соответствующая эпюра нормальных напряжений (МПа) в аксонометрии.
5.4.2. Содержание задачи на внецентренное сжатие.

30
Для заданной короткой стойки требуется:
определить координаты центра тяжести, выразив все величины через характерные размеры сечения;
вычислить главные моменты и радиусы инерции заданного сечения стойки;
выразить отрезки, отсекаемые на главных осях инерции, нейтральной линией и построить
ее;
из условия прочности материала на растяжение и сжатие определить размеры поперечного сечения, если Rсж расчетное сопротивление материала на сжатие, Rp то же, на растяжение;
найти нормальные напряжения в угловых точках сечения стойки и построить эпюру в аксонометрии;
построить ядро сечения.
Варианты задач взять из таблиц.
Пример расчета короткой стойки на внецентренное сжатие
Для стойки, загруженной в точке I силой Р = 1,0 МН, определить размеры сечения при Rсж = 200 МПа, Rp = 75 МПа, b/h =7/16.
Р=10 МH
G
a) |
|
|
L |
Е |
|
|
|
F |
K |
(I) |
|
|
|
H |
|
|
|
C3 |
|
|
D |
|
|
|
|
|
|
|
B |
|
|
|
|
A |
|
б)
P=1 MН
Рис.5.8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1. Разбивка заданного сечения на простые площади F1, F2, F3 c указанием собственных |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
центральных осей xi, yi (i=1, 2, 3) |
(Рис.5.8б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
F |
1 |
|
6 |
|
b |
h |
|
|
3 |
|
bh; |
|
EGF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
2 |
|
7 |
|
|
4 |
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
F |
|
|
6 |
b |
h |
|
3 |
|
bh; |
|
|
|
|
|
|
|
|
|
|
|
EGKD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
7 |
|
|
|
|
|
2 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
F |
14 |
b |
h |
|
7 |
bh bh; |
|
|
|
BLHA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
7 |
|
|
|
|
|
|
2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
F Fi |
3 bh 3bh bh 37bh. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2. Координаты центров тяжести составляющих площадей относительно |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вспомогательной оси х0: |
1 |
|
|
|
h |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
h |
|
h |
|
|
|
|
3 |
|
|
|
|
|
|
h |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
1 |
|
h |
|
|
h; |
y |
2 |
|
|
|
|
h; |
y |
3 |
|
. |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
12 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||||||||||||||
|
|
3. Вычисление координаты центра тяжести, лежащего на оси симметрии у: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Sx |
|
|
|
|
|
|
|
|
Fy |
|
|
F y |
|
|
F y |
|
|
|
|
|
3 |
bh |
11 |
h |
3 |
bh |
3 |
h bh |
h |
|
|
53 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
28 |
|
|
|
12 |
|
|
7 |
|
4 |
|
|
|
|
|
h 0,358h. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
c |
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 F2 |
|
F3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |
bh |
|
|
|
|
|
148 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Главные центральные оси показаны на рис. 5.9б.
4. Вычисление значений квадратов радиусов инерции относительно главных центральных осей х, у через главные моменты инерции соответственно:
|
|
|
|
|
|
6 |
|
|
|
h |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 h |
3 |
|
|
|
|
|
|
|
|
|
h |
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
11 |
|
|
53 |
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
b |
|
|
|
|
3 |
|
53 |
|
2 |
3 |
|
2b |
|
|
|
||||||||||||
|
|
|
|
|
|
7 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||
Ix |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
h |
|
|
|
|
|
bh |
|
|
|
|
|
|
|
|
|
h |
|
|
h |
|
|
bh |
|
|
|
|
||||||||||||
36 |
|
|
|
|
12 |
|
148 |
|
|
|
|
|
12 |
|
4 |
148 |
7 |
12 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
h |
|
53 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
bh 0,07347bh |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
148 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
6 |
|
|
3 |
|
|
h |
|
6 |
|
|
|
3 |
|
|
|
|
h |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
2b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
7 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Iy |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
0,3563hb3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
48 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
i |
2 |
|
|
I |
x |
|
|
|
0,07347bh3 28 |
|
0,0556h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
x |
|
F |
|
|
|
|
|
|
37bh |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
Iy |
|
|
|
|
|
0,3563hb3 28 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
i |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2696b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
37bh |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5. Определение положения нейтральной линии отрезками, которые отсекает она на главных центральных осях инерции по формулам (5.6):
|
|
i2y |
|
0,2696b2 |
||||||
xN |
|
|
|
|
|
|
|
|
|
0,2696b |
xp |
|
b |
|
|||||||
|
|
|
|
|
|
|
||||
yN |
|
i2 |
|
0,0556h |
2 |
0,5146bh. |
||||
x |
|
|
|
|||||||
yp |
|
|
|
|||||||
|
|
|
|
|
0,108h |
|||||

32
На рис. 5.10 показано положение нейтральной линии. Нейтральная линия делит сечение на две зоны: в одной растягивающие, в другой сжимающие напряжения. Видно, что в сжатой зоне опасной является точка Н, а в растянутой точка В. Из условия прочности материала в этих точках определим требуемые размеры b и h сечения короткой стойки.
6. Определение размеров поперечного сечения из условия прочности:
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
xpxH |
|
ypyH |
|
|
|
|
|
|
|
|
||||||||
|
|
а) у |
H |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Rсж |
|
|
|
|||||||||||||
|
|
|
2 |
2 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iy |
|
ix |
|
|
|
|
|
|
|
|
|
|
|||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,108h 0,358h |
|||||||
|
|
|
|
|
|
|
|
|
|
|
28P |
|
|
|
|
|
b b |
|
|
|
||||||||||||||||
|
|
уH |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Rсж |
|||||||||||
|
|
|
|
|
|
|
|
|
0,2696b 2 |
|
|
|
|
|
|
0,0556h 2 |
||||||||||||||||||||
|
|
|
|
|
|
7 |
|
|
37bh |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
откуда при |
b |
h: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
16 |
|
|
28P 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
уH |
|
|
|
|
(5,4) |
Rсж |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
37 16b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
уH 1,788 |
|
|
P |
|
|
|
|
Rсж. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,788 1000 10 |
3 |
|
|
|
|
|
|||||||||
|
|
|
1,788 P |
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||
Откуда b |
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
9,45 см |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
R–с |
|
|
|
|
|
|
|
|
|
|
200 10 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
h |
(1) |
|
16 |
b |
(1) |
21,62см. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
28P 7 |
|
|
(b) ( b) |
|
( 0,108h)(0,142h) |
|
|
|||||||||||||
б) у |
B |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
R |
p |
||||||||
|
37 16b2 |
|
0,2696b2 |
|
|
|
0,0556h2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
уB 0,988 |
|
P |
Rp |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,988 1000 103 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0,988P |
|
|
|
2 |
|
|
|
|
|||||||||||||||
b |
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
11,5 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Rp |
|
|
|
|
|
|
|
|
75 10 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
h |
(2) |
|
16 |
b |
(2) |
|
11,50 |
16 |
26,24см. |
|
|
||||||||
|
7 |
|
|
7 |
|
||||
Окончательно принимаем размеры b = b(2) = 11,5 см, h = h(2) = 26,50 см.
7. Определение нормальных напряжений в угловых точках контура поперечного сечения стойки и построение эпюры напряжений в аксонометрии. Применяем формулу (5.4)
|
|
|
P |
|
xpxi |
|
ypyi |
|
у |
i |
|
|
1 |
|
|
|
|
|
2 |
2 |
||||||
|
|
F |
|
|
|
|||
|
|
|
|
iy |
|
ix |
|
Так для точки B имеем:
|
|
|
28P |
|
|
xpxB |
|
ypyB |
|
|
|
|
28 |
1,0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
уB |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
37bh |
2 |
|
2 |
37 26,30 |
11,5 10 |
4 |
|||||||||||||
|
|
|
|
|
|
iy |
|
|
ix |
|
|
|
|
|
|||||
|
|
(b)( b) |
|
|
( 0,108h)(0,142h) |
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
74,12МРa < Rp |
75МРa. |
||||
0,2696b2 |
|
|
0,0556h2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
