КЛ Спец констр МК

максимальних значень різних навантажень, які розглядаються одночасно, або дій. Правила введення цих коефіцієнтів визначаються нормами.

В деяких випадках необхідно забезпечити який-небудь степінь надійності роботи матеріалу конструкції. Для цього вводять коефіцієнт надійності за матеріалом.

Необхідно брати до уваги відхилення дійсної роботи конструкцій від розрахункових припущень, що приймаються у проекті. Це враховують через введення коефіцієнта умов роботи.

За другим граничним станом конструкції розраховують від нормативних навантажень з коефіцієнтами перевантаження, що дорівнюють одиниці, за винятком розрахунку переміщень в рухливих опорних частинах і деформаційних швах, коли ці коефіцієнти приймають більше за одиницю.

Навантаження і дії беруть у найбільш невигідних при експлуатації і будівництві можливих положеннях і сполученнях для кожного елемента, що розраховується, частини конструкції або всієї споруди в цілому.

2.6. Проблема утоми

Враховуючи, що мости сприймають динамічні дії, особлива увага при проектуванні і конструюванні мостів надається проблемам витривалості (утоми). Перш за все всі з'єднання та вузли металевих і сталебетонних конструкцій розраховуються на проектний термін служби. На підставі цих розрахунків визначаються терміни оглядів та ремонтів. У процесі виготовлення конструкцій всі зварні з'єднання піддаються ультразвуковому і (або) рентгенівському контролю. Уникають місць концентрації напружень шляхом спеціальних конструктивних заходів: шліфуванням зварного шва та основного металу, усуненням бовтозварних з'єднань, усуненням сталей великої товщини, зварних пакетів і т.п.

ЛІТЕРАТУРА:

1.СНиП 2.05.03-84. Мосты и трубы/Госстрой ССР.-М.:ЦИТП Госстроя СССР, 1985,

2000с.

2.СНиП III-43-75. Правила производства и приемки работ. Мосты и трубы / Госстрой СССР.- М.: ЦИТП Госстроя СССР, 1976, 110 с.

3.СНиП 3.06.07-86. Мосты и трубы. Правила обследований и испытаний. / Госстрой

СССР.- М.: ЦИТП Госстроя СССР, 1988, 40 с.

4.Інструкція по утриманню штучних споруд / В.Ф. Сушков, Л.П. Ватуля, М.М. Літвінов та інші. – К.: Транспорт України, 1999.-96 с.

5.Гибшман Е.Е. Проектирование металлических мостов. — М.: Транспорт, 1969.— 415

с.

6.Стрелецкий Н.Н. Сталежелезобетонные пролетные строения мостов. — М.:

Транспорт, 1981. — 359 с.

7.Стан та залишковий ресурс фонду будівельних металевих конструкцій в Україні. / А.В. Перельмутер, В.М. Гордеєв, Є.В. Горохов та ін. – К.: “Сталь”, 2002.- 166 с.

111

РОЗДІЛ 7. ЧИСЕЛЬНІ МЕТОДИ АНАЛІЗУ

КОНСТРУКЦІЙНИХ СИСТЕМ

(автор: д.т.н., професор Мущанов В.П.)

Лекція 1.

1. Основні положення. Терміни і визначення. Переваги і недоліки

Розрахунок складних конструкційних систем може виконуватися як аналітичними, так і чисельними методами. Проте ефективність застосування аналітичних методів, не дивлячись на можливість отримання розв'язання в зручному замкнутому вигляді, залежить від того, наскільки вдало підібрані апроксимуючі вирази. У зв'язку з цим обмеженням розрахунок конструкційних систем аналітичними методами (Власова, Рітца-Тимошенко, БубноваГальоркіна і др.) здійснюється, як правило, для конструкцій з простою геометрією поверхні, класичними граничними умовами (шарнірно-нерухоме закріплення або жорстке закладення ), осесиметричні розподілені навантаження.

У зв'язку з бурхливим розвитком обчислювальної техніки особливо широке застосування отримали чисельні методи: метод кінцевих різниць, метод кінцевих елементів, варіаційнорізницевий метод і ін.

2.МКР. Область застосування. Особливості застосування в розрахунках стержньових і просторових листових конструкцій

Основна ідея методу кінцевих різниць (МКР) полягає в заміні диференціальних рівнянь кінцево-різницевими, які приводять до системи рівнянь алгебри щодо невідомих дискретних значень шуканих функцій у вузлових точках сітки.

Нехай наприклад, дана функція двох змінних F=F(х,у) і треба обчислити часткову похідну F / x у вузлі і. Якщо АВ є дотична до поверхні F = F(х,у) у вузлі і, паралельна площині xy, то точне значення похідної дорівнює тангенсу кута (tg) нахилу прямої до осі х. Наближене значення похідної можна отримати, якщо замість прямої АВ розглянути пряму А1В1; а тангенс кута нахилу прямої А1В1 приблизно буде являти собою першу похідну в точці і:

F Fl Fkx 2h

Принципова послідовність рішення задачі методом кінцевих різниць має наступний вигляд:

1.Записується система диференціальних рівнянь, що описують напруженодеформований стан конструкції.

2.На поверхню конструкції, що розраховується, з кроком h наноситься сітка вузлів густиною 4 х 4 ... 8 х 8 (див. Рис. 1).

3.Обчислюємо значення функції і її похідних в суміжних точках відповідно до нижченаведених формул (наприклад, формули для заміни першої або другої похідних для

112

точок і, n) і замінюємо, тим самим, початкову систему диференціальних рівнянь системою рівнянь алгебри.

4. Розв’язуємо систему алгебраїчних рівнянь і визначаємо значення шуканої функції (величини переміщень, напружень і т.д.) у всіх вузлах сітки.

пружності, тобто розв'язанню ряду задач напружено-деформованого стану тонколистових металевих конструкцій, для яких характерний плоский напружений стан. Як відомо, рішення плоскої задачі теорії пружності описується диференціальним рівнянням 4-го порядку (бігармонічним рівнянням Лапласа):

113

4 x, y x44 2 x2 4y2 y44 x,y 0

де x,y - шукана функція напруг (функція Ері).

В результаті використовування кінцево-різницевих виразів, представлених в п.3, і приведення подібних членів для точки і - n отримаємо алгебраїчні рівняння наступного вигляду

20 i,n 8 i 1,n i 1,n i,n 1 i,n 1 2 i 1,n 1 i 1,n 1 i 1,n 1 i 1,n 1

i 2,n i,n 2 i 2,n i,n 2 0

Записуючи представлене рівняння для інших точок сітки одержуємо систему алгебраїчних рівнянь, розв’язуючи які (за умови попереднього визначення значень функції напружень в контурних і законтурних точках сітки), отримуємо значення функції напружень

у вузлах сітки.

Як основні недоліки МКР слід зазначити:

-незручність дослідження елементів із змінним перерізом зважаючи на ускладнення системи початкових диференціальних рівнянь;

-значні труднощі в складанні нерегулярних сіток;

наближене урахування граничних умов.

При всіх своїх достоїнствах (простоті, достатньо великій універсальності і т.п.) застосування МКР безпосередньо до початкових рівнянь при складних граничних умовах може привести до помітних погрішностей. У зв'язку з цим на даний час особливо широке застосування серед всіх чисельних методів знайшов метод кінцевих елементів (МКЕ).

Лекція 2.

1. Особливості використання МКЕ в розрахунках листових конструкцій

Застосування МКЕ пов'язане з цілим рядом важливих для даного випадку переваг:

-можливість представляти велику кількість конструктивних елементів заданими аналітичними моделями - кінцевими елементами, і мати, тим самим, широку область аналітичного уявлення;

-при розрахунку за МКЕ можуть бути розглянуті граничні умови і навантаження довільного характеру;

-розміри, а також жорсткісні характеристики кінцевих елементів, можуть бути змінними залежно від геометрії конструкції, а також конструктивних, експлуатаційних, технологічних особливостей;

-властивості матеріалів елементів, які становлять конструкцію, можуть бути різними, що дозволяє розраховувати конструкції, які складаються з різномодульних матеріалів.

В той час як при розв'язанні задач, пов'язаних із статичним розрахунком стрижньових конструкцій, МКЕ дає точні розв'язання, то при використанні в розрахунках просторових

114

листових (континуальних) систем ці рішення носять наближений характер. Точність результатів розрахунку залежить, перш за все, від густини сітки. При цьому для розрахунків на розподілені навантаження, наприклад, покриттів мембран з гнучким опорним контуром, рекомендується сітка не менше, ніж 24 х 24. Для мембран з практично незміщуваним опорним контуром густина сітки може бути знижена до 12 ... 16.

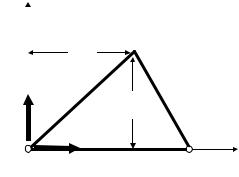
Для розрахунку конструкцій, що випробовують плоский напружений стан, плоский трикутний кінцевий елемент являється одним з найбільш зручних типів кінцевих елементів, оскільки дозволяє найбільш просто і зручно отримати на конструкції сітку вузлів необхідної густини. Розглянемо процес формування матриці жорсткості плоского трикутного 3-и вузлового кінцевого елемента з вузлами і, j, m, позначеними у напрямі обходу проти годинникової стрілки (див. Рис. 2)

y1

m xm

vi

ym

Зміщення у вузлі мають 2 компоненти - ui і vi. Тоді вектор вузлових зміщень елемента може бути представлений як

(1)

Найпростіше представлення зміщень u і v точок з координатами х і у в середині елемента через зміщення вузлових точок може бути отримано на основі використання двох лінійних многочленів:

Підставивши рішення систем (3) у вирази (2) остаточно отримаємо вирази для u і v

115

Коефіцієнти aj, bj, cj, am, bm, cm можна отримати шляхом циклічної перестановки індексів в послідовності і, j, m.

Відносна деформація в будь-якій точці елемента визначається за допомогою трьох компонентів, що вносять внесок у внутрішню роботу, яка за допомогою рівнянь (4) може бути записана як

Ураховуючи, що для трикутного елемента постійної товщини загальний вираз для матриці жорсткості може бути спрощений, тобто

k e B T D B dV B T D B t

і ураховуючи, що матриця пружності (закон Гука) для випадку плоского напруженого стану має вигляд

остаточно вираз для матриці жорсткості плоского трикутного елемента має вигляд:

116

де

Надалі використання матриці жорсткості трикутного кінцевого елемента нічим не відрізняється від використання матриці жорсткості стрижньового кінцевого елемента, що описано в попередньому розділі.

Іншою яскраво вираженою особливістю застосування МКЕ в розрахунках листових просторових конструкцій є урахування можливості сприйняття тонким металевим листом стискальних зусиль. До цього часу сформувалися три основні напрями, в яких різними авторами по-різному оцінюється можливість сприйняття тонким металевим листом стискальних напружень:

1 - мембрана здатна сприймати стискальні зусилля нарівні з розтягальними; 2 - мембрана не сприймає стискальних напружень;

3 - часткове сприйняття стискальних зусиль при ортогональному розтягуванністисненні .

Перерозподіл зусиль в мембрані після виключення з роботи стиснутої ділянки досліджувався в основному двома методами:

а) шляхом згущування сітки вузлів і задання початкових вигинів; б) шляхом задання "умовно" ортотропної розрахункової моделі із зниженою

жорсткістю мембрани у напрямі стискувальних напружень.

Ступінь умовної анізотропії в роботах приймався: 0.5 - 0.7 - для гіпара, 0.25 - для шатрової, 0.1 - 0.2 - для плоскої мембрани, ненавантаженої в поперечному напрямі, яка працює на зсув; 0.15 - для плоскої мембрани за наявності поперечного навантаження.

На даний час запропоновані алгоритми:

1)засновані на використанні ітераційного процесу і стрижньової апроксимації мембрани з урахуванням пониження жорсткості стиснутих елементів шляхом множення жорсткості на розтягування на коефіцієнт граничного стиснення (до k= 0.25 для циліндрової поверхні).

2)засновані на використанні прийомів задання початкових вигинів (наприклад, при сітці 12 х 12 максимальна величина початкового вигину 1 мм).

117

РОЗДІЛ 8. МЕТОДИ ВАРІАНТНОГО І ОПТИМАЛЬНОГО

ПРОЕКТУВАННЯ СПЕЦІАЛЬНИХ СПОРУД

(автори: к.т.н., доцент Роменський І.В., д.т.н., професор Мущанов В.П.)

1.Цілі, задачі, загальні принципи оцінки економічної ефективності конструктивної форми. Основні положення, терміни і визначення

Метою оцінки економічної ефективності конструктивної форми є вибір рішення, що дає найбільший економічний ефект при обов'язковому виконанні вимог міцності, надійності, довговічності.

При виборі і обґрунтовуванні проектних рішень, оцінки їхнього технічного рівня, урахування властивостей конструкції з погляду економічних інтересів різних учасників будівельного циклу використовують систему техніко-економічних показників (ТЕП).

Техніко-економічні показники можуть відноситися до будівельного об'єкту в цілому, окремих складових його підсистем (об'ємно-планувальні, конструктивні, технологічні і т.д.) або елементів (колони, балки, ферми і т.д.). Можливі ТЕП, які відносяться до окремих фрагментів конструкції, наприклад вузлів спряження елементів.

Головними задачами оцінки економічної ефективності конструктивної форми є:

-вибір кращого варіанта з деякого числа альтернативних;

-формування цільової функції для вибору економічно оптимального варіанта, тобто кращого при заданих умовах і обмеженнях.

Під техніко-економічною оцінкою розуміють виконання розрахунків встановленого набору показників, що характеризують варіанти проектних рішень і виявлення їхньої економічної ефективності. В результатах техніко-економічної оцінки повинно бути відображено вплив технічних, технологічних, організаційних, ринкових чинників на економічні показники проектних рішень. Суть техніко-економічної оцінки полягає: в глибокому і всесторонньо му вивченні різноманітних чинників, комплексно урахованих при розробці проектів; кількісному визначенні показників, що характеризують варіанти; зіставленні показників між собою з метою вибору найкращого проектного рішення.

Загальні принципи техніко-економічної оцінки.

1. В основі визначення ефективності проектного рішення повинен бути народногосподарський підхід. Необхідно добиватися зниження прямих і спряжених витрат на будівництво, поточних витрат при експлуатації об'єкту, раціонального використовування земель, що відводяться під будівництво, зменшення негативних технологічних дій на навколишнє середовище і т.д.

2. Комплексність оцінки. Техніко-економічна оцінка проектних рішень повинна проводитися на всіх основних стадіях їхньої розробки. Проектувальник повинен вибрати склад визначуваних ТЕП і критерій оцінки варіантів, що зіставляються, виходячи із поставленої задачі. На даний час це особливо важливо, оскільки економічні інтереси кожного з учасників будівельного циклу неоднакові. Відповідні економічні інтереси і господарські умови пов'язані з різними ТЕП і критеріями ефективності. Ухвалюючи технічне

118

рішення, проектувальник повинен ясно уявляти собі його оцінку для всіх зацікавлених осіб і організацій будівельного циклу. Стосовно металевих конструкцій будівельний цикл розділений на етапи: виготовлення, транспортування, монтаж, експлуатація. Ці етапи виконуються різними організаціями. Послідовність дій при техніко-економічній оцінці в загальному вигляді показана на рис.1 /1/.

3.При оцінці проектних рішень використовується метод порівняльної економічної ефективності. Зіставляються показники витрат і встановлюється наскільки один варіант більш ефективний від іншого. Для усесторонньої оцінки проектних рішень використовується система показників. Один з показників звичайно приймається як головний, а інші ураховуються як додаткові. Аналіз окремих показників використовується для виявлення шляхів вдосконалення варіантів або з метою розкрити можливі погрішності при визначенні показників. Техніко-економічні показники діляться на абсолютні і відносні, вартісні і натуральні. Склад абсолютних показників наведений на рис.2 /2/.

4.Для правильної оцінки порівнюваних варіантів необхідне дотримання умов зіставності. Варіанти повинні бути зіставлені за: функціональним призначенням; ступенем детальності проектних опрацьовувань; за рівнем використовуваних при проектуванні норм, правил, ТУ (будівельні конструкції повинні бути розраховані на однакові навантаження, для однакових умов експлуатації); рівнем цін і кошторисно-нормативної бази; технічним рівнем виготовлення і зведення; методам обчислення техніко-економічних показників (початкові дані повинні бути зіставними по складом, величиною, одиницями вимірювання, точністю). Порівняння варіантів слід проводити тільки з погляду ознак які відрізняють їх. Однакові для варіантів елементи до розгляду не включаються. Показники по суміжних частинах проекту, не залежні від особливостей даного рішення приймаються умовно однаковими. У випадках, коли особливості альтернативних варіантів обумовлюють зміни в інших частинах проекту (наприклад, зміна витрат на стінове обгороджування, опалювання, вентиляцію і т.д.), слід ураховувати різницю у витратах на будівництво і поточних витратах по змінних суміжних частинах.

Основні терміни і визначення.

Варіант — одне з альтернативних проектних рішень, розроблених відповідно до поставленої задачі. Проектне рішення, яке відповідіє сучасному технічному рівню і поширене в практиці, називається аналогом.

Довговічність, термін служби будівлі, споруди, конструкції — час функціонування, після якого використовування стає технічно неможливим (фізичний термін служби) або нераціональним (моральний термін служби).

Витрати — обсяг ресурсів, витрачених для досягнення результату. Критерій — правило переваг при відборі варіантів рішень.

Оптимальне рішення — краще проектне рішення із усіх можливих за заданим критерієм.

Показник — ознака, що відображає кількісні і якісні властивості об'єкту.

Проектне обмеження — наперед встановлене замовником і (або) регламентуючою документацією обмеження, в т.ч. за величиною техніко-економічних показників.

119

Ресурси — витрати праці, матеріалів, енергії, асигнувань і часу, необхідного для створення і експлуатації об'єкту.

Економічність проекту — категорія, що відображає ідею економії по всіх позиціях витрат, пов'язаних із створенням і експлуатацією об'єкту.

При проектуванні металевих конструкцій розглядається система техніко-економічних показників, що характеризують якість проектного рішення і технологічність конструкції з погляду витрат у галузі будівництва (рис. 2). Розглянемо більш детально ці показники.

Маса металу конструкції. Найбільш вживаний показник при оцінці проектних рішень. Легко розраховується. У складі вартості конструкції витрати на метал складають 50…70%. Крім того, вага металу істотно впливає на трудомісткість і вартість виготовлення і монтажу. Проте, буде помилковим вважати масу узагальнюючим показником. Не всі складові витрат залежать від маси. Залежність витрат від маси може бути нелінійна і навіть розривна. Це пов'язано з тим, що при зміні маси змінюється технологія. Малому діапазону зміни витрат на метал може відповідати більший діапазон зміни витрат на виготовлення, монтаж, експлуатацію.

Витрати на матеріали при виготовленні включають витрати на металопрокат з урахуванням відходів, зварювальні і лакофарбі матеріали, розраховані за діючими цінами. Цей показник ураховує відмінності, зв'язані з використанням сталей різних марок, варіанти антикорозійних покриттів. В порівнянні з масою показник залежить не тільки від параметрів конструкції, але і від ринкової кон'юнктури.

Трудомісткість заводського виготовлення — сума витрат праці на виконання технологічних процесів виготовлення. Є числовою характеристикою властивостей конструкції, узагальнюваних поняттям технологічність. Вона не залежить від ринкової кон'юнктури і пов'язана з параметрами конструктивної форми, технологією виготовлення, оснащеністю виробництва. Технологічний процес розділяється на технологічні операції, що виконуються на відповідному їм робочому місці. Трудомісткість представляє суму трудовитрат по окремих технологічних операціях. Трудовитрати, безпосередньо не пов'язані з технологічними процесами виготовлення, ураховуються непрямим чином в показниках собівартості виготовлення. Так само, як і маса, трудомісткість — фізична величина.

Заводська собівартість виготовлення — сума витрат (в грошовому виразі) на виготовлення і реалізацію конструкції. Включає: витрати на матеріали; заробітну плату виробничих і допоміжних робочих, ІТР, службовців; витрати на тримання і експлуатацію устаткування (амортизація, ремонт, енерговитрати тощо) і інструментів; загальноцехові витрати; загальнозаводські витрати; поза виробничі витрати. Вплив кон'юнктури виявляється через ціни на матеріали і заробітну плату.

Ціна конструкції — сума, за яку її продає завод-виготівник . Різниця між ціною і заводською собівартістю є прибутком заводу-виготівника . При зіставленні проектних рішеньціна конструкції не вносить нічого нового в порівнянні з собівартістю.

Транспортні витрати включають витрати на перевезення від заводу заготівника до приоб’єктного складу в районі будівництва. Представляють інтерес у разі значних відмінностей у цих витратах для варіантів рішень, що може бути пов'язане із: збільшенням відстані перевезення через спеціалізацію заводів-виготівників ; зміною виду транспортних засобів; появою негабаритності вантажу і т.д.

120