МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ

Кафедра высшей и прикладной математики и информатики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к самостоятельной работе по курсу «Вычислительная техника и программирование» Часть 1. Методы решения систем уравнений. Метод Гаусса

(для студентов строительных специальностей дневной формы обучения)

УТВЕРЖДЕНО на заседании кафедры

высшей и прикладной математики и информатики

Протокол № 2 от 16.09.2004 г.

Макеевка 2004 г.

3

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Инженеру часто приходится решать алгебраические и трансцендентные уравнения, что может представлять собой самостоятельную задачу или являться частью более сложных задач. В обоих случаях практическая ценность метода в значительной мере определяется быстротой и эффективностью полученного решения.

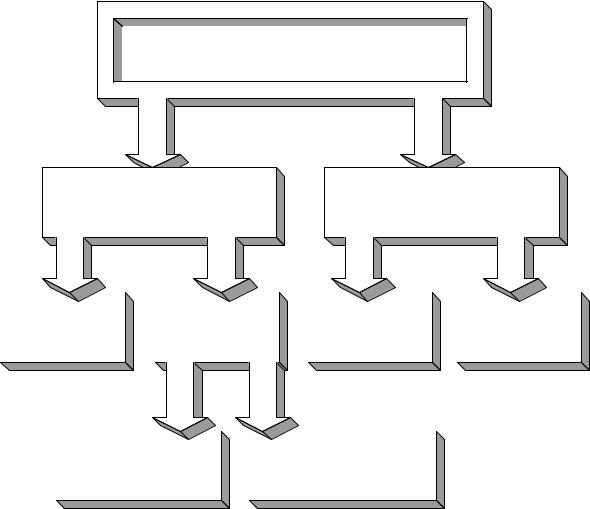
Выбор подходящего метода для решения уравнений зависит от характера рассматриваемой задачи. Задачи, сводящиеся к решению алгебраических и трансцендентных уравнений, можно классифицировать по числу уравнений и в зависимости от предлагаемого характера и числа решений (Рис. 1.).

Рис. 1. Классификация уравнений и систем уравнений в зависимости от числа решений

Любое уравнение с одним неизвестным может быть записано в виде: f (x )= 0

Если функция f (x) представлена многочленом первой степени, т.е. уравнение имеет вид:

4

f (x)= a x + b = 0 ,

то такое уравнения называется линейным и оно имеет одно решение x = −ab .

Если функция f (x) представлена многочленом n -ой степени, т.е. уравне-

ние имеет вид:

f (x)= an xn + an−1 xn−1 + ...+ a1 x + a0 = 0 ,

то такое уравнение называется алгебраическим. Алгебраическое уравнение n - ой степени имеет n корней, считая и комплексные корни.

Если функция f (x) содержит в себе тригонометрические, логарифмиче-

ские или показательные функции, то соответствующее уравнение называется трансцендентным. Такое уравнение может иметь как конечное, так и бесконечное число решений.

Систему уравнений будем называть линейной или нелинейной в зависимости от математической природы входящих в нее уравнений.

Решение линейного уравнения с одним неизвестным получается достаточно просто и здесь не рассматривается.

Концепция методов

Способы решения систем линейных уравнений делятся на две группы:

•точные (прямые) методы, представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, метод Крамера, метод Гаусса и др.), т.е. при использовании таких методов за конечное число действий получаем точное решение системы. Точное решение получается в том случае, если вычисления проводить без округлений, т.е. понятие точное относится к алгоритму решения.

•итерационные (приближенные) методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов

(метод итерации, метод Зейделя и др.).

Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода.

Эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.

В общем виде линейная система уравнений записывается следующим образом:

или чаще в матричном виде: a x = B , где а – квадратная матрица размером n x n, B и x – векторы размером n (n – размерность системы).

5

Метод Гаусса

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х1, х2, …, хn:

Метод Гаусса, его еще называют методом Гауссовых исключений (методом последовательных исключений), состоит в том, что систему (1) приводят последовательным исключением неизвестных к эквивалентной системе с верхней треугольной матрицей:

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду:

а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:

Последний, (n+1) столбец этой матрицы содержит решение системы (1). Рассмотрим изложенное более подробно.

Верхняя треугольная система линейных уравнений

Рассмотрим алгоритм обратной подстановки, который полезен для решения систем линейных уравнений, имеющих верхнюю треугольную матрицу коэффициентов.

6

Доказательство.

Решение можно легко найти. Последнее уравнение включает только одно неизвестное xN , поэтому вычисляем его первым:

Когдазначения xN , xN −1 ,K, xk +1 известны, можнозаписатьобщуюформулу:

N

bk − ∑ akj x j

Легко видеть, что решение единственно.

Метод исключения Гаусса и выбор главного элемента

Рассмотрим схему решения системы A x = B N уравнений с N неизвестными. Нашей целью является построение эквивалентной верхней треугольной системы α x = β , которую можно решить методом обратной подстановки.

7

Говорят, что две линейные системы размера N x N эквивалентны, если они имеют одно и то же множество решений. Теоремы из линейной алгебры показывают, что применение определенных преобразований к заданной системе не изменяет множества решений.

Теорема (элементарные преобразования). Следующие операции, приме-

ненные к линейной системе, приводят к эквивалентной системе.

Чаще всего используют замещение, чтобы заменить уравнение разностью между этим уравнением и кратным другому уравнению. Рассмотрим это на примере

Пример. Найдем параболу y = A + B x +C x2 , которая проходит через

три точки: (1; 1), (2; -1), (3; 1).

Для каждой точки найдем уравнение связывающее значение x со значением y . Результатом является система линейных уравнений:

Если вычесть первое уравнение из второго и третьего, то исключается переменная А. Это применение преобразования замещения. В результате получаем эквивалентную линейную систему.

Переменная В исключается из третьего уравнения (11) путем двукратного вычитания из него второго уравнения. Получается эквивалентная верхняя тре-

Воспользуемся алгоритмом обратной подстановки для нахождения коэффициентов: C = 4 / 2 = 2 ; B = −2 − 3 2 = −8 ; A = 1 −( −8 ) − 2 =7 . Следователь-

но уравнение параболы имеет вид: y =7 −8 x + 2 x2 .

Эффективнее всего можно хранить коэффициенты линейной системы A x = B как матрицу размера N х (N+1). Коэффициенты В хранятся в (N+1)-м

8

столбце матрицы. Расширенная матрица обозначается как A B , и систему уравнений представляют в виде:

К расширенной матрице также можно применять операции согласно вышеизложенной теореме об элементарных преобразованиях.

Определение (главный элемент). Коэффициент arr матрицы А, который используется, чтобы исключить элементы akr , где k = r + 1, r + 2,K, N , назы-

вается r -м главным (ведущим) элементом и r -я строка – главной строкой.

Пример. Представить следующую систему в форме расширенной матрицы, найти эквивалентную ей верхнюю треугольную систему линейных уравнений и ее решение

x1 +2 x2 + x3 +4 x4 =13

−3 x1 + x2 +3 x3 +2 x4 = 6

Первая строка используется, чтобы исключить элементы под диагональю в первом столбце. Мы обращаемся к первой строке, как к главной, и называем

Вторая строка используется, чтобы исключить элементы под диагональю во втором столбце. Эта строка является главной, и значение mk 1 является мно-

жителем строки 2, которую вычитаем из k строк, k = 3,4 . Результатом исключения будет:

9

Описанный выше процесс называется методом исключения Гаусса и должен быть модифицирован так, чтобы его можно было использовать в большинстве случаев. Если akk = 0 , то строку k нельзя использовать для исключения

элементов столбца k и строку k следует заменить такой же строкой под диагональю, чтобы получить не равный нулю главный элемент. Если этого нельзя сделать, значит, матрица коэффициентов системы линейных уравнений является вырожденной и система не имеет единственного решения.

Рассмотрим решение системы в общем виде на примере системы 4 уравнений с 4 неизвестными:

Первый шаг. Выберем ведущий элемент первого шага, отличный от 0. Если a11 ≠ 0 , то возьмем его за ведущий на первом шаге, если равен 0, то переста-

вим уравнения в системе так, чтобы a11 ≠ 0 .

Разделим первое уравнение на ведущий элемент a11 , получим уравнение:

Исключим x1 из остальных уравнений системы, сложив их с первым, умноженным, соответственно, на −ai 1 (i ≥ 2). Для коэффициентов при x2 , x3 , x4 введем обозначение:

10

aij(1) = aij − ai 1 a1(1j) , (i , j ≥ 2)

Рассмотрим систему:

Взяв последние три уравнения, получим систему трех уравнений с тремя неизвестными:

В системе (16) разделим первое уравнение на a22(1) ≠ 0 для выделения x2 (если a22(1) = 0 , то меняем уравнения местами):

Отсюда уже можно найти x4 .

На этом заканчивается прямой ход. Легко усмотреть общий вид формул пересчета коэффициентов для прямого хода:

Формула (21) – для ведущих уравнений, а (22) – для остальных.

Таким образом, в результате прямого хода получена верхняя треугольная система из уравнений (15), (17), (19) и (20) из которой можно найти:

11