
- •Мазмұны
- •1.2 Жалпы түсініктер
- •1.2 Қалдықпен бөлу
- •1.3 Ең үлкен ортақ бөлгіш және ең кіші ортақ еселік
- •Мунда жазу керек
- •1.4 Сандар теорясының негізгі теоремасы
- •2. Бөлінгіштікке қатысты қалыпты емес есептер
- •2.1 Математикалық индукция әдісі. Ньютон биномының формуласы.
- •2.2 Бөлінгіштік белгілері
- •2.3 Көбейткіштерге жіктеу формулаларын қолдану
- •2.4 Қалдықпен бөлу
- •2.5 Өзара жай сандар
2.3 Көбейткіштерге жіктеу формулаларын қолдану
7. 2020 цифрдан тұратын 1000 . . . 001 санының 1001 санына бөлінетінін дәлелдеңіз.
Шешуі. Берілген санды келесідей түрлендірейік:

673 тақ сан болғандықтан берілген сан 1001 санына бөлінеді.
8.
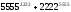 қосындысының 7-ге бөлінетінін дәлелдеңіз.
қосындысының 7-ге бөлінетінін дәлелдеңіз.
Шешуі.
Берілген
қосындыны
 арқылы белгілеп, оны келесі түрінде
жазайық
арқылы белгілеп, оны келесі түрінде
жазайық
Оң
жақтағы әр жақшадағы қосындыны Ньютон
биномы бойынша жіктесек онда,
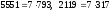 болатындықтан, әр жіктеудегі соңғы
қосылғыштан басқа қосылғыштардың 7-ге
бөлінетіндігін көреміз. Яғни,
болатындықтан, әр жіктеудегі соңғы
қосылғыштан басқа қосылғыштардың 7-ге
бөлінетіндігін көреміз. Яғни, Енді
Енді қосындысының 7-ге бөлінетіндігін
көрсетсек жеткілікті.
қосындысының 7-ге бөлінетіндігін
көрсетсек жеткілікті.
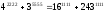 болатындықтан,
соңғы қосындының
болатындықтан,
соңғы қосындының
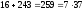 санынына бөлінетіндігін көреміз.
Сонымен, берілген сан 7-ге бөлінеді.
санынына бөлінетіндігін көреміз.
Сонымен, берілген сан 7-ге бөлінеді.
9.
Кез келген натурал
 үшін
үшін қосындысының 9-ға бөлінетінін дәлелдеңіз.
қосындысының 9-ға бөлінетінін дәлелдеңіз.
Шешуі.
Берілген
қосындыны
 түрінде жазайық.
түрінде жазайық.
Ньютон
биномы бойынша жіктесек, онда
 қосындысы 9-ға қалдықсыз бөлінсе, онда
берілген қосындының да 9-ға бөлінетінін
көру қиын емес.
қосындысы 9-ға қалдықсыз бөлінсе, онда
берілген қосындының да 9-ға бөлінетінін
көру қиын емес. қосындысын
келесідей түрлендірейік:
қосындысын
келесідей түрлендірейік:
 .
.
Ал
 қосындысы 9-ға бөлінетіндіктен,
қосындысы 9-ға бөлінетіндіктен,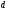 қосындысы да 9-ға бөлінеді. Демек,
берілген қосынды 9-ға бөлінеді.
қосындысы да 9-ға бөлінеді. Демек,
берілген қосынды 9-ға бөлінеді.
10.
Егер
 тақ сан болса
тақ сан болса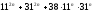 қосындысының 40-қа бөлінетінін
дәлелдеңіз.
қосындысының 40-қа бөлінетінін
дәлелдеңіз.
Шешуі. Берілген қосындыны келесідей түрлендірейік:
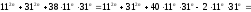

 .
.
Ал
 тақ сан болғанда
тақ сан болғанда айырымы 20-ға бөлінетінін ескерсек,
онда бірінші және екінші қосылғыш 40-қа
бөлінетіндіктен, олардың қосындысы да
40-қа бөлінеді.
айырымы 20-ға бөлінетінін ескерсек,
онда бірінші және екінші қосылғыш 40-қа
бөлінетіндіктен, олардың қосындысы да
40-қа бөлінеді.
11.
 қосындысының 66-ға бөлінетінін
дәлелдеңіз.
қосындысының 66-ға бөлінетінін
дәлелдеңіз.
Шешуі. Берілген қосындыны келесідей түрлендірейік:
 .
.
Бірінші
жақшадағы қосынды
 санына бөлінетіндігі айқын. Екінші
жақшадағы айырымды формула бойынша
түрлендірсек, келесі өрнекті аламыз:
санына бөлінетіндігі айқын. Екінші
жақшадағы айырымды формула бойынша
түрлендірсек, келесі өрнекті аламыз:
 .
.
Бұл
көбейтіндінің
 және
және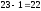 сандарына бөлінетіндігін көреміз.
Сондықтан, ол 66-ға да бөлінеді.
сандарына бөлінетіндігін көреміз.
Сондықтан, ол 66-ға да бөлінеді.
12.
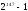 санынын 343-ке бөлінетінін дәлелдеңіз.
санынын 343-ке бөлінетінін дәлелдеңіз.
Шешуі.
Беріген
айырымды
көбейткіштерге
жіктейік. Сонда,
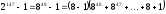 болады.
болады.
 болғандықтан,
болғандықтан,
 қосындысының
49-ға бөлінетінін көрсетсек жеткілікті.
Ол үшін әрбір
қосындысының
49-ға бөлінетінін көрсетсек жеткілікті.
Ол үшін әрбір
 қосылғыштыНьютон
биномы формуласымен жіктейік. Сонда,
әр жіктеудегі соңғы қосылғыш 1-ден өзге
қосылғыштардың 7-ге бөлінетінін көреміз.
Ал, 1-лердің саны 49 болғандықтан,
қосылғыштыНьютон
биномы формуласымен жіктейік. Сонда,
әр жіктеудегі соңғы қосылғыш 1-ден өзге
қосылғыштардың 7-ге бөлінетінін көреміз.
Ал, 1-лердің саны 49 болғандықтан,
 қосындысы
49-ға бөлінеді.
қосындысы
49-ға бөлінеді.
2.4 Қалдықпен бөлу
13.
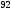 -ге
бөлінетін, ал
-ге
бөлінетін, ал -ға бөлгенде 3 қалдық қалатын ең кіші
натурал
-ға бөлгенде 3 қалдық қалатын ең кіші
натурал
 санын
анықтаңыз.
санын
анықтаңыз.
Шешуі.
 десек, онда
десек, онда Бұл теңдікті
Бұл теңдікті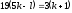 түрінде жаза аламыз.
түрінде жаза аламыз. және
және сандары өзара жай сандар болғандықтан
сандары өзара жай сандар болғандықтан

Осыдан,
 Яғни,
Яғни, .
.
14.
 тақ сан және 3-ке бөлінеді.
тақ сан және 3-ке бөлінеді.
 санын 6-ға бөлгендегі қалдықты анықтаңыз.
санын 6-ға бөлгендегі қалдықты анықтаңыз.
Шешуі.
Есеп
шарты бойынша
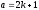 және
және .
. санын 6-ға бөлгендегі қалдық
санын 6-ға бөлгендегі қалдық болсын. Онда
болсын. Онда Жоғарыдағы теңдіктерден
Жоғарыдағы теңдіктерден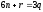 болады. Осыдан
болады. Осыдан Теңдіктің оң жағындағы өрнек 3-ке
бөлінетіндіктен сол жағындағы өрнек
те 3-ке бөлінуі керек. 6-ға бөлгендегі
қалдық 1, 2, 3, 4, 5 болатындықтан
Теңдіктің оң жағындағы өрнек 3-ке
бөлінетіндіктен сол жағындағы өрнек
те 3-ке бөлінуі керек. 6-ға бөлгендегі
қалдық 1, 2, 3, 4, 5 болатындықтан
15.
 санын 3-ке бөлгендегі қалдық 1-ге, ал 4-ке
бөлгендегі қалдық 3-ке тең.
санын 3-ке бөлгендегі қалдық 1-ге, ал 4-ке
бөлгендегі қалдық 3-ке тең. санын 6-ға және 12-ге бөлгендегі қалдықты
анықтаңыз.
санын 6-ға және 12-ге бөлгендегі қалдықты
анықтаңыз.
Шешуі.
Есеп шарты бойынша
 және
және .
Онда
.
Онда немесе
немесе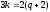 .
2 мен 3 өзара жай сандар болғандықтан
.
2 мен 3 өзара жай сандар болғандықтан жұп сан.
жұп сан. болса, онда жоғарыдағы теңдіктерден
болса, онда жоғарыдағы теңдіктерден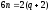 немесе
немесе болады. Онда
болады. Онда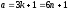 және
және немесе
немесе .
Демек, 6-ға бөлгенде 1 қалдық, ал 12-ге
бөлгенде 7 қалдық қалады.
.
Демек, 6-ға бөлгенде 1 қалдық, ал 12-ге
бөлгенде 7 қалдық қалады.
16. (3.29)
17. Цифрларының қосындысы 5-ке бөлінетін 1-мен 1999 сандарының аралығында қанша бүтін сан бар?
Шешуі.
Төрт
орынды
сандарды
 түрінде өрнектейік.
түрінде өрнектейік. қосындысын 5-ке бөлгендегі қалдық келесі
сандардың бірі болуы мүмкін: 0, 1, 2, 3, 4.
Осы қалдықтарға сәкес,
қосындысын 5-ке бөлгендегі қалдық келесі
сандардың бірі болуы мүмкін: 0, 1, 2, 3, 4.
Осы қалдықтарға сәкес, -ны
санның цифрларының
қосындысы
5-ке
бөлінетіндей етіп анықтайық.
-ны
санның цифрларының
қосындысы
5-ке
бөлінетіндей етіп анықтайық.
|
Қалдықтың мәні |
0 |
1 |
2 |
3 |
4 |
|
с-ның мәні |
0 немесе 5 |
4 немесе 9 |
3 немесе 8 |
2 немесе 7 |
1 немесе 6 |
Демек,
әр қалдыққа қатысты, есеп шартын
қанағаттандыратындай
 -ның
мәндері екеу.
-ның
мәндері екеу.
1-мен
1999 сандарының аралығында бір таңбалы
5 саны ғана есеп шартын қанағаттандырады.
Екі таңбалы сандарды
 деп белгілесек, мұндағы
деп белгілесек, мұндағы 1-ден 9-ға дейінгі тоғыз цифрлардың бірі.
Яғни, цифрларының қосындысы
5-ке
бөлінетін екі орынды
сандардың саны
1-ден 9-ға дейінгі тоғыз цифрлардың бірі.
Яғни, цифрларының қосындысы
5-ке
бөлінетін екі орынды
сандардың саны
 .
.
Үш
орынды
сандарды
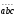 деп белгілесек, мұндағы
деп белгілесек, мұндағы -ның
қабылдайтын мәндері 1-ден 9-ға дейінгі
тоғыз цифрлар болса,
-ның
қабылдайтын мәндері 1-ден 9-ға дейінгі
тоғыз цифрлар болса, -ның
қабылдайтын мәндері 0-ден 9-ға дейінгі
он цифр. Яғни, үшорынды
сандардың ішіндегі
-ның
қабылдайтын мәндері 0-ден 9-ға дейінгі
он цифр. Яғни, үшорынды
сандардың ішіндегі
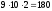 сан есеп шартын қанағаттандырады. Осы
сияқты, төрторынды
сандар
сан есеп шартын қанағаттандырады. Осы
сияқты, төрторынды
сандар
 болса,
болса,
 мен
мен
 -ның
әрқайсысының қабылдайтын мәндері 0-ден
9-ға дейінгі он цифр болатындықтан,
-ның
әрқайсысының қабылдайтын мәндері 0-ден
9-ға дейінгі он цифр болатындықтан,
 төрт
орынды
санның цифрларының
қосындысы
5-ке
бөлінеді.
төрт
орынды
санның цифрларының
қосындысы
5-ке
бөлінеді.
Сонымен,
1-мен 1999 сандарының аралығында цифрларының
қосындысы
5-ке
бөлінетін
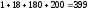 сан бар.
сан бар.
