
- •Содержание
- •Введение
- •1.Обзор работ по резонансным ударно-вибрационным машинам
- •1.1 Общие сведения о виброуплотняющих машинах и областях их применения
- •1.2 Динамика резонансных ударно-вибрационных машин
- •2. Анализ динамики ударно-вибрационных систем
- •2.1 Обоснование расчетной схемы ударно-вибрационной системы с двумя степенями свободы на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами
- •2.2 Динамика ударно-вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами
- •2.3 Анализ результатов исследования динамики вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами.
- •Выводы по разделу
- •3. Методика расчета двухмассной резонансной ударно-вибрационной системы с двумя степенями свободы
- •3.1 Расчет резонансной ударно-вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами.
- •3.2 Выводы по разделу
- •Заключение
Выводы по разделу
1. Предложены упрощенные математические модели двухмассных ударно-вибрационных машин с упругими ограничителями с центробежным приводом и с эксцентриково-шатунным приводом.
2. Разработка программы расчета двух массных ударно вибрационных машин, позволяющая находить их основные параметры и фазовые соотношения.
3.
Установлена закономерность для всех
двухмассных ударно-вибрационных машин
с упругими ограничителями, состоящая
в том, что при резонансном режиме работы
фазовые углы
 между
вынуждающей силой и переходом скорости
через нуль зависит только от соотношения
коэффициентов жесткости упругих
ограничителей и постоянных упругих
связей и величины зазора.
между
вынуждающей силой и переходом скорости
через нуль зависит только от соотношения
коэффициентов жесткости упругих
ограничителей и постоянных упругих
связей и величины зазора.
4.
Найденные зависимости дает возможность
использовать систему автоматического
фазового регулирования по выбору фазовых
углов
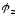 в зависимости от соотношения
в зависимости от соотношения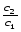 и зазораh.
и зазораh.
3. Методика расчета двухмассной резонансной ударно-вибрационной системы с двумя степенями свободы
3.1 Расчет резонансной ударно-вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами.
Для двухмассной ударно-вибрационной виброплощадки с центробежным приводом исходными данными при резонансе являются:
 масса
рабочего органа;
масса
рабочего органа;
 частота
вынуждающей силы;
частота
вынуждающей силы;
 максимальное
ускорение рабочего органа.
максимальное
ускорение рабочего органа.
Целесообразно
предварительно используя результаты
приближенных исследований системы
уравнений, определить значения
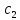 и
и – жесткости основных упругих элементов
и ограничителя;S
– статический момент массы дебаланса;
– жесткости основных упругих элементов
и ограничителя;S
– статический момент массы дебаланса;
 масса первого тела.
масса первого тела.
Согласно [15] расчет производных производим в следующем порядке:
На основе опыта конфигурирования и эксплуатации машин принимаем

Жесткость постоянных упругих связей:

где
 собственная частота колебаний системы
с
собственная частота колебаний системы
с
упругими
связями,
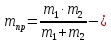 приведенная масса системы;
приведенная масса системы;
 собственная
частота колебаний с суммарной жесткостью
упругих связей
собственная
частота колебаний с суммарной жесткостью
упругих связей
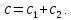
Жесткость упругих ограничителей:

Максимальная деформация упругих ограничителей:
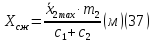
Используя прямую линеаризацию, находим статический момент массы дебалансов (кг
 м),
при котором выдерживается принятое
значение
м),
при котором выдерживается принятое
значение

Считая, что рассеивание мощности происходит только в той части периода движения, когда деформирован упругий ограничитель, мощность необходимая для поддержания колебаний в системе соответствует:

где
h
– коэффициент затухания; h
= (0,8 )
)
Мощность приводного электродвигателя:

где
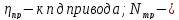 мощность
затрачиваемая на трение:
мощность
затрачиваемая на трение:

где
 приведенный к валу коэффициент трения
скольжения подшипника качения (при
жидкой смазке),d
– диаметр шейки вала под подшипником.
приведенный к валу коэффициент трения
скольжения подшипника качения (при
жидкой смазке),d
– диаметр шейки вала под подшипником.
По
выражениям для
 задавшись числом упругих элементов и
ограничителей, находят коэффициент
жесткости одного элемента. Расчет
резиновых ограничителей производят с
учетом их максимальной деформации при
ударе. По выражению дляS,
задавшись числом дебалансов, находят
статический момент массы одного
дебаланса. Далее определяют его
геометрические размеры.
задавшись числом упругих элементов и
ограничителей, находят коэффициент
жесткости одного элемента. Расчет
резиновых ограничителей производят с
учетом их максимальной деформации при
ударе. По выражению дляS,
задавшись числом дебалансов, находят
статический момент массы одного
дебаланса. Далее определяют его
геометрические размеры.
При исследовании колебаний системы в области резонанса очень важен учет рассеяния энергии в упругих элементах.
Внутреннее трение определяется рядом факторов, влияние которых очень сложно. Наибольшее распространение получила гипотеза вязкого трения. Она предлагает, что диссипативные силы пропорциональны скорости деформации упругих связей. Рассеяние энергии в нелинейных упругих связях можно представить функцией:

где
 кусочно
– постоянная функция;
кусочно
– постоянная функция;
 коэффициенты
жесткости упругих связей.
коэффициенты
жесткости упругих связей.

где
h
– зазор в буферах;
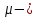 коэффициент
внутренних сопротивлений, для резиновых
ограничителей
коэффициент
внутренних сопротивлений, для резиновых
ограничителей По рекомендации [18] рассеяние энергии
в резиновых упругих связях в (2
По рекомендации [18] рассеяние энергии
в резиновых упругих связях в (2 )
раза выше, чем остальных.
)
раза выше, чем остальных.
После ориентировочного расчета основных параметров системы, можем провести уточнение их с использованием программы ASSVM.
Покажем
на численном примере последовательность
определения основных параметров двух
массной ударно-вибрационной площадки.
Известна масса рабочего органа
 максимальное ускорение рабочего органа
задано
максимальное ускорение рабочего органа
задано
Принимаем
величину
 равной:
равной:

2. Жесткость постоянных упругих связей:


где
 в
соответствии с [11].
в
соответствии с [11].
3. Жесткость упругих ограничителей:

4. Статический момент массы дебалансов:



5. Значения коэффициентов сопротивлений принимаем по рекомендациям в работах [15], [17].
Суммарные
значения коэффициента сопротивления
упругих элементов постоянной подвески
массы
 и обрабатываемой среды принимаем равным
и обрабатываемой среды принимаем равным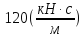 .
.
Имеем

 .
.
Значения
жесткостей опорных упругих элементов
 принимается по условию их прочности,
принимается по условию их прочности,
Будем
проводить расчет машины с нулевым
ударным зазором. При не деформированных
пружинах с коэффициентом жесткости

Используя
программу, задавшись шагом
 получаем данные для построения
зависимостей
получаем данные для построения
зависимостей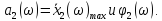
Эти зависимости показаны на (рис. 9, кривые 1,1е). Из графика видно, что резонанс достигается при частоте вынуждающей силы
 ,
то есть отклонение от предварительной
заданной резонансной частоты составляет:
,
то есть отклонение от предварительной
заданной резонансной частоты составляет:

Фазовый
угол

Решение нелинейных дифференциальных уравнений, описывающих динамику машины с эксцентриково – шатунным приводом с упругими элементами в шатуне, осложняются тем, что они не интегрируемы в квадратурах. Поэтому приходится идти по пути широкого применения приближенных методов.
В данном методе при нахождении первого приближения осуществляется эквивалентная линеаризация. Причем частота собственных колебаний и декремент затухания линеаризованной системы являются функциями амплитуды периодической составляющей деформации основных упругих связей и амплитуды деформации приводов элементов.
Динамика резонансной ассиметричной вибрационной площадки, соответствующей расчетной схеме на (рис. 8), хорошо изучена[18]. Там же приведены методика расчета резонансных асимметричных вибрационных площадок, которая дает возможность выбрать параметры системы. Исходные данные для расчета таких машин являются:
а)
предела изменения минимального ускорения
 рабочего органа;
рабочего органа;
б) асимметрия закона движения рабочего органа

где
 ,
, - максимальные и минимальные ускорения
рабочего органа;
- максимальные и минимальные ускорения
рабочего органа; -
выбирается из технологических соображений
-
выбирается из технологических соображений ;
;
в)
диапазон рабочих частот
 вынуждающей силы;
вынуждающей силы;
г)
масса рабочего органа
 ;
;
Далее, руководствуясь [18], определим основные параметры вибрационной площадки:
масса
 уравновешивающей рамы равно:
уравновешивающей рамы равно: ;
;коэффициенты формы колебаний:
 ;
;амплитуда
 периодической составляющей деформации
основных упругих связей связана с
амплитудой
периодической составляющей деформации
основных упругих связей связана с
амплитудой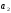 колебаний
рабочего органа соотношением:
колебаний
рабочего органа соотношением:
 ;
;
смещение центра колебаний относительного положения статического равновесия
 при нулевом зазоре в буферах:
при нулевом зазоре в буферах:
 ,
,
где
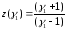 ;
;
величина жесткости линейных основных упругих связей:
 ,
,
где,
 - приведенная масса системы;
- приведенная масса системы;
жесткость упругого ограничителя определяется выражением:
 ;
;
эксцентриситет приведенного вала следует принимать:
 ;
;
частота вынуждающей силы определяется как:
 ,
,
для следующего случая нулевого зазора в буферах:
при
 ,
, ,
[18];
,
[18];
жесткость опорных упругих элементов выбирается минимально возможной по условиям их прочности;
жесткость приводных упругих связей выбирается как:

где,

Рассмотрим численный пример предварительного определения основных параметров двух массной вибрационной площадки.
Пусть
нам известно:
 ;
; ;
; ;
;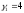 ;
; .
.
примем значение

 ;
; .
.
коэффициент формы колебания определим по формуле:
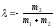 ;
;
 ;
;
приведены масса системы определения как:
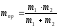 ;
;
 ;
;
амплитуда
 периодической
составляющей деформации основных
упругих связей определяется соотношением:
периодической
составляющей деформации основных
упругих связей определяется соотношением:
 ;
;
 ;
;
смещение центра колебаний относительно положения статического равновесия для зазора в буферах найдем как:
 ,
,
 ;
;
 ;
;
 ;
;
жесткость линейных основных упругих связей будет равна:
 ;
;
 ;
;
жесткость ограничителя должна удовлетворять соотношению:
 ;
;
 ;
;
эксцентриситет приводного вала примем равным:
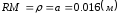
частота вынуждающей силы:
 ;
;
 ;
;
где
 -
для нулевого зазора в буфере при
-
для нулевого зазора в буфере при равно:
равно:
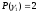 ,[18].
,[18].
жесткость приводных упругих связей выбирается как:
 ,
,
где
 ,
,

 -максимальная
масса рабочего органа,
-максимальная
масса рабочего органа,
 ;
;


По
рекомендациям [15] принимаем
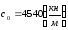 ;
;
значение в коэффициентах сопротивлений принимаются на основании данных [15],[18]:
 ;
;
Коэффициенты
сопротивления опорных элементов
 :
:

Коэффициенты
сопротивления ограничителя
 ;
;

Результаты
расчета вибрационной площадки с
эксцентриково –шатунным
приводом с помощью компьютерного
моделирования позволяют построить
графики зависимости
 и
и .
.
Из
(рис. 11) видно, что максимальное ускорение
достигаются при частоте вынуждающей
силы
 ,
то есть отклонение от предварительно
определяемой частоты составляет:
,
то есть отклонение от предварительно
определяемой частоты составляет: и максимальное ускорение рабочего
органа
и максимальное ускорение рабочего
органа соответствует отклонению:
соответствует отклонению: от
первоначально принятого.
от
первоначально принятого.
