32

Глава 9. Статистическое изучение связи социально-экономических явлений

9.1. Методические указания и решения типовых задач

Особенности статистического изучения связи между социально-экономическими явлениями заключаются в том, что они дают возможность не только выявить наличие и направление связи, но позволяют количественно ее оценивать и выражать аналитически. Связи между явлениями и признаками ввиду большого их разнообразия классифицируются в статистике по ряду оснований. Признаки по характеру их роли во взаимосвязи подразделяются на факторные (x)ирезультативные (y). Факторные признаки обуславливают изменение других, связанных с ними признаков. Признаки, изменяющиеся под действием факторных признаков, называются результативными.

Связи между явлениями, их признаками подразделяют, прежде всего, по степени тесноты связи, по направлению и ее аналитическому выражению. Речь идет о полной, или функциональной, связи и связи неполной, корреляционной или статистической. Функциональными называются такие связи, в которых определенному значению факторного признака (признаков) соответствует строго определенное значение результативного признака. В корреляционной (статистической) же связи такого соответствия между изменением факторного признака и результативного нет – одному и тому же значению признака-фактора могут соответствовать разные значения результативного признака (при одном и том же размере внесения органических удобрений урожайность зерновых культур может иметь самые различные значения). Корреляционная связь проявляется лишь в среднем, в массе случаев.

По направлению выделяют связь прямую и обратную. Прямая – это такая связь, при которой оба вида признаков (факторный и результативный) изменяются в одном и том же направлении – по мере увеличения или уменьшения значения факторного признака значения результативного соответственно увеличиваются или уменьшаются. В случае же обратной связи значения результативного признака изменяются под действием факторного, но в противоположном направлении по сравнению с изменением факторного признака. Так, с увеличением надоев молока на одну корову уровень его себестоимости при прочих равных условиях, как правило, снижается.

По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные. Если статистическая связь явлений может быть приближенно выражена математическим уравнением прямой линии, то ее называют линейной связью, если же она может быть выражена уравнением кривой линии (параболы, гиперболы, полулогарифмической кривой и т.п.), то криволинейной.

Для выявления связи, ее характера, направления в статистике используются методы приведения параллельных данных, балансовый, аналитических группировок, графический. Суть метода приведения параллельных данных состоит в следующем: приводятся два ряда данных о двух явлениях или двух признаков, связь между которыми необходимо выявить, и по характеру изменений делают заключения о наличии (если изменение величин одного ряда следует за изменением величин другого ряда) или об отсутствии связи (если никакого твердого, устойчивого соответствия в их изменениях нет). Балансовый метод заключается в построении балансов-таблиц, в которых итог одной части равен итогу другой (например, баланс производства сахара и его потребления).

Посредством факторных группировок устанавливаются и изучаются причинно-следственные связи между факторными и результативными признаками. Они основаны на изучении того, как в массовых явлениях с изменением одного или нескольких факторных признаков изменяется результативный признак. Например, с увеличением размера внесенных органических удобрений средняя урожайность зерновых культур от группы к группе закономерно возрастает.

Характер зависимости между двумя признаками (факторным и результативным) можно наглядно увидеть, если построить график, отложив на оси абсцисс ранжированные (возрастающие) значения признака-фактора (x), а на оси ординат значения результативного признака (y). Нанеся на график точки, соответствующие значениям x и y, получим корреляционное поле, где по характеру расположения точек можно судить о направлении и силе связи. Если точки беспорядочно разбросаны по всему полю, это говорит о том, что зависимости между двумя признаками нет; если они будут концентрироваться вокруг оси, идущей от нижнего левого угла в верхний правый, то имеется прямая зависимость между варьирующими признаками; и если точки будут концентрироваться вокруг оси, идущей от верхнего левого угла в нижний правый, то имеется обратная зависимость.

Удобной формой изложения данных о взаимосвязанных признаках является корреляционная таблица, представляющая собой комбинационную статистическую таблицу, в которой сопрягаются ряды распределения факторного и результативного признаков. Если частоты концентрируются у диагонали, идущей из левого верхнего угла в правый нижний, то это указывает на то, что связь между факторными и результативными признаками близка к прямой, а если же в корреляционной таблице частоты концентрируются у диагонали, идущей из правого нижнего угла в верхний левый, то в подобных случаях отмечается обратная связь между признаками.

Показатели тесноты связи. Для оценки тесноты связи применяется ряд показателей. Одни из них являются эмпирическими (непараметрическими), другие - теоретическими (выводимыми строго математически).

К непараметрическим коэффициентам оценки тесноты связи относятся: коэффициент Фехнера (коэффициент знаков), коэффициент корреляции рангов (коэффициент Спирмена), коэффициент конкордации, коэффициент ассоциации, коэффициент контингенции и коэффициент взаимной сопряженности.

Коэффициент знаков (коэффициент Фехнера) вычисляется на основании определения знаков отклонений вариантов двух взаимосвязанных признаков от их средних величин по формуле:

, (9.1)

где С – число совпадений знаков;

Н – число несовпадений знаков.

Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывает по рангам (порядковым номерам) двух взаимосвязанных признаков следующим образом:

, (9.2)

где d_i² – квадраты разности рангов; n – число наблюдений (число пар рангов).

Пример 1. По данным группам сельскохозяйственных предприятий района о внесении органических удобрений (x, т/га) и уровнем урожайности зерновых культур (y, ц/га) рассчитаем коэффициент Спирмена:

Таблица 9.1

№ предп-риятия	x	y	Сравнение рангов		Разность рангов di=Rx-Ry	di2
			Rx	Ry
1	2	22	2	1	1	1
2	1	23	1	2	-1	1
3	3	25	3,5	3	0,5	0,25
4	3	28	3,5	5	-1,5	2,25
5	4	27	5	4	1	1
6	5	30	6	6,5	-0,5	0,25
7	7	32	8	8	0	0
8	6	30	7	6,5	0,5	0,25
9	8	35	9,5	10	-0,5	0,25
10	8	34	9,5	9	0,5	0,25
Итого	-	-	-	-	-	6,5

Следовательно, связь между размером внесения органических удобрений и уровнем урожайности зерновых культур прямая и тесная.

Если двум или нескольким показателям присвоен один и тот же ранг, то расчеты производятся как средняя арифметическая из порядковых значений рангов.

Для определения тесноты связи между тремя признаками применяется ранговый коэффициент конкордации, который вычисляется по формуле:

, (9.3)

где m – число признаков; n – число наблюдений; S- сумма квадратов отклонений рангов.

Пример 2. Наряду с вышеприведенной задачей определить тесноту связи между размером внесенных органических удобрений (x, т/га); размером внесенных минеральных удобрений (z, кг/га) и уровнем урожайности зерновых культур (у, ц/га). Зависимость между признаками представлена в табл. 9.2.

Таблица 9.2

№ предприятия	х	z	y	Сравнение рангов			Сумма рангов Rx+Rz+Ry	Квадраты сумм
				Rx	Rz	Ry
1	2	100	22	2	1	1	4	16
2	1	120	23	1	2	2	5	25
3	3	150	25	3,5	4	3	10,5	110,25
4	3	140	28	3,5	3	5	11,5	132,25
5	4	160	27	5	5	4	14	196
6	5	170	30	6	7	6,5	19,5	380,25
7	7	165	32	8	6	8	22	484
8	6	180	30	7	8	6,5	21,5	462,25
9	8	200	35	9,5	10	10	29,5	870,25
10	8	190	34	9,5	9	9	27,5	756,25
Итого	-	-	-	-	-	-	165	3432,5

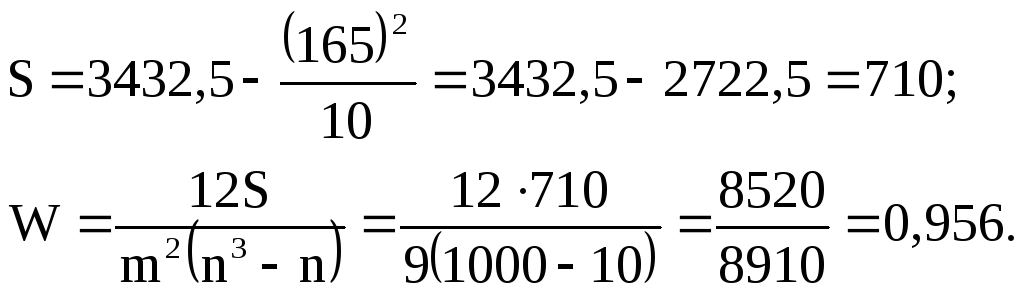
Величина коэффициента конкордации показывает, что между исследуемыми признаками имеется тесная зависимость. Эта зависимость объясняется тем, что рассматриваемые факторы оказывают значительное влияние на уровень урожайности зерновых культур.

Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным.

Коэффициент ассоциации исчисляется по формуле:

(9.4)

где a, b, c, d – частоты клеток четырехпольной таблицы, а коэффициент контингенции рассчитывается:

(9.5)

Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если

Пример 3. Исследовалась связь между выполнением норм выработки рабочих и уровнем их образования. Результаты обследования характеризуются следующими данными:

Таблица 9.3

Группы рабочих	Выполняющие нормы	Не выполняющие нормы	Итого
Рабочие, имеющие среднее техническое образование	80 (а)	20 (b)	100
Рабочие, не имеющие среднего технического образования	30 (c)	70 (d)	100
Итого	110	90	200

Связь между выполнением норм выработки и уровнем образования рабочих признается достоверной.

Если каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи применяется коэффициент взаимной сопряженности К.Пирсона. Этот коэффициент исчисляется по формуле:

(9.6)

где - показатель взаимной сопряженности.

Пример 4. В качестве примера расчета коэффициента взаимной сопряженности возьмем аналитическую таблицу, характеризующую связь между урожайностью ячменя и сроками его уборки.

Таблица 9.4

Урожайность Сроки сева	Высокая	Средняя	Низкая	Итого	Ti
Своевременно	50 2500 41,67	8 64 2,56	2 4 0,27	60 - 44,50	0,742
С небольшим опозданием	10 100 1,67	14 196 7,84	6 36 2,40	30 - 11,91	0,397
С сильным опозданием	_	3 9 0,36	7 49 3,27	10 - 3,63	0,363
Итого	60	25	15	100	1,502

Порядок заполнения клеток корреляционной таблицы производится следующим образом. В левом верхнем углу каждой клетки проставляются частоты, в центре клетки рассчитаны квадраты частот, внизу справа каждой клетки записываются частные от деления квадратов частот на суммы по соответствующей графе. Так, например, 41,67 есть результат деления (2500 : 60); 2,56 (64 : 25); 0,27 (4 : 15) и т.д. Сумма этих чисел проставляется в нижнем углу первой клетки итоговой графы:

41,67 + 2,56 + 0,27 = 44,50.

Таким же образом производится подсчет сумм и в других клетках итоговой графы. Частные от деления найденных сумм на итог частот по каждой строке заносятся в клетки последней графы (Т_i). И наконец, сумма чисел последней графы без единицы и равна, т.е.

Подставив найденное значение в формулу расчета коэффициента взаимной сопряженности, получим:

Коэффициент взаимной сопряженностиисчисляется и по формуле, предложенной А.А. Чупровым:

(9.7)

где К₁ – число групп по факторному признаку;

К₂ – число групп по результативному признаку.

Вычислим коэффициент взаимной сопряженности по формуле А.А. Чупрова:

Корреляция и регрессия. На основе методов корреляционно-регрессионного анализа представляется возможным оценить не только тесному связи, но и выразить эту связь аналитически.

Связь между результативным и факторным признаками в зависимости от ее характера может быть аналитически выражена уравнениями:

прямой: (9.8)

с системой нормальных уравнений:

(9.9)

гиперболы: ; (9.10)

с системой нормальных уравнений:

(9.11)

параболы второго порядка: (9.12)

с системой нормальных уравнений:

(9.13)

степенной функции: (9.14)

для нахождения системы нормальных уравнений необходимо выражение степенной функции прологарифмировать, т.е.:

(9.15)

с системой нормальных уравнений:

(9.16)

Уравнение полулогарифмической кривой:

(9.17)

с системой нормальных уравнений:

(9.18)

В уравнении прямой параметр а₀ показывает влияние на результативный признак неучтенных факторов. Параметр а₁ – коэффициент регрессии показывает, на сколько в среднем изменяется значение результативного признака при увеличении факторного на единицу его измерения. В уравнении параболы а₂ показывает ускорение (замедление) результативного признака при увеличении факторного признака на единицу.

На основе коэффициентов регрессии вычисляются коэффициенты эластичности, которые показывают изменение результативного признака (y) в процентах в зависимости от изменения факторного признака (x) на 1%.

При линейной зависимости запишем:

(9.19)

а если зависимость представлена в виде параболы, то коэффициент эластичности имеет вид:

(9.20)

Уравнение регрессии как бы доводит метод группировок до каждой единицы наблюдения.

Для измерения тесноты связи при линейной зависимости служит линейный коэффициент корреляции, исчисляемый по формуле:

(9.21)

В случае нелинейной зависимости между признаками линейный коэффициент корреляции теряет смысл и для измерения тесноты связи применяют так называемое корреляционное отношение, известное также под названием «индекс корреляции», исчисляемый по формуле:

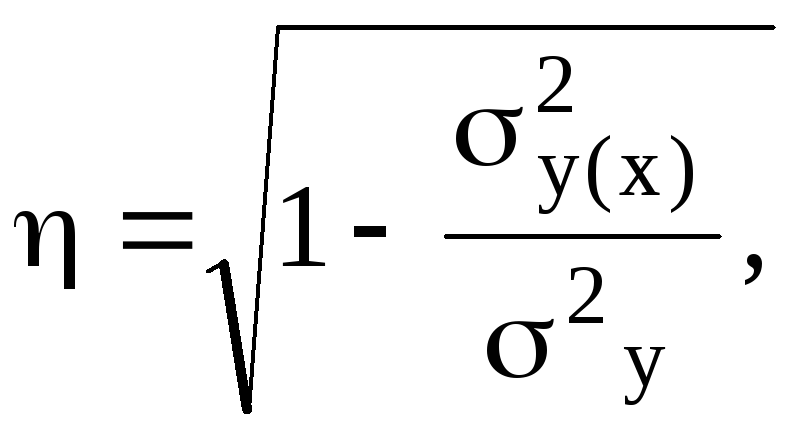(9.22)

где (9.23)

Для качественной оценки связи на основе показателя корреляционного отношения можно пользоваться следующей таблицей, предложенной американским ученым Чэддоком:

Таблица 9.5

Величина η	0,1 - 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,99
Сила связи	слабая	умеренная	заметная	высокая	очень высокая

Для оценки значимости коэффициента корреляции используют критерий, исчисляемый по формуле:

(9.24)

где - среднеквадратическая ошибка коэффициента парной корреляции:

(9.25)

Если , то существование связи между признаками признается доказанным, и наоборот.

Пример 5.По данным о стоимости основных фондов (х, млрд. р.) и объеме выпуска продукции (у, млрд. р.) необходимо определить уравнение связи и тесноту связи. Связь предполагается линейной.

Таблица 9.6

№ предприятия	х	у	ху	х2	у2
1	120	56	6720	14400	3136	52,2
2	80	40	3200	6400	1600	35,4
3	100	40	4000	10000	1600	43,8
4	60	24	1440	3600	576	27,0
5	90	36	3240	8100	1296	39,6
6	150	50	7500	22500	2500	64,8
7	110	46	5060	12100	2116	48,0
8	130	65	8450	16900	4225	56,4
9	140	70	9800	19600	4900	60,6
10	100	45	4500	10000	2025	43,8
Итого	1080	472	53910	123600	23974	471,6

Применительно к уравнению прямой запишем систему нормальных уравнений:

10а₀+1080а₁=472;

1080а₀+123600а₁= 53910;

а₀= 1,8; а₁= 0,42;

Следовательно, с увеличением стоимости основных фондов на 1 млрд. р. объем выпуска продукции увеличивается в среднем на 0,42 млрд. р.

Определим коэффициент эластичности:

то есть с увеличением стоимости основных фондов на 1% объем выпуска продукции увеличивается на 0,96%.

Для вычисления коэффициента корреляции необходимо рассчитать:

(9.26)

(9.27)

(9.28)

(9.29)

Рассчитаем величину линейного коэффициента корреляции:

=.

Вычислим критерий существенности коэффициента корреляции:

Поскольку t_эмп > 3, то существенность связи между размером основных фондов и объемом выпуска продукции признается доказанной.

Значения параметров уравнения прямой можно вычислить на основе статистических характеристик:

Следовательно:

Оценка значимости (существенности) коэффициента корреляции может быть осуществлена с использованием критерия Стьюдента: если t_эмп.>t_табл., то существенность связи доказана, и наоборот. Значение t_табл. определяется с уровнем значимости, допустим, = 0,05 и числом степеней свободы V = n –m, где n – число наблюдений; m – число параметров уравнения (Приложение 2). В нашем примере имеем: V = 10 – 2 = 8, тогда t_табл ( = 0,05, V = 8) = 2,3.

Поскольку t_эмп.>t_табл, то существенность связи между исследуемыми признаками статистически подтверждена.

Оценка значимости коэффициента регрессии а₁ осуществляется следующим образом: если то с заданным уровнем значимостиможно статистически констатировать подтверждение существенности коэффициента регрессии а₁. Эмпирическое значение критерия коэффициента регрессии определятся по формулам:

(9.30)

где 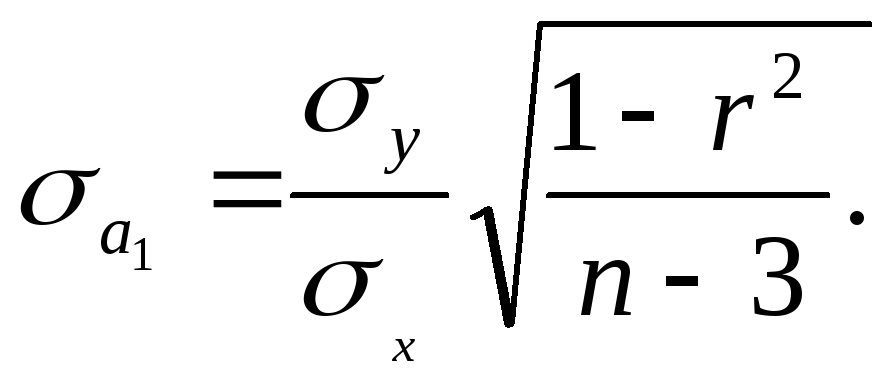(9.31)

Вычислим значение :

Эмпирическое значение критерия коэффициента а₁:

Табличное значение критерия коэффициента регрессии совпадает с определением этого значения для коэффициента корреляции, т.е. . Посколькуто значимость (существенность) коэффициента регрессии (а₁) статистически доказана.

Измерение тесноты связи по уравнению параболы второго порядкавозможно в тех случаях, когда функция имеет экстремальные значения (максимум или минимум), то есть точки перегиба. Так, например, с увеличением размеров внесения органических удобрений уровень урожайности зерновых культур возрастает, но до определенного предела. Достигнув его, урожайность уже не растет и даже падает. Такая связь между признаками вполне обоснована может быть описана уравнением параболы второго порядка:

(9.32)

На основе уравнения параболы второго порядка можно определить значение факторного признака (х), при котором значение результативного признака (у) достигнет максимума. Для этого используется формула:

(9.33)

Пример.6.Исследуется влияние размера внесенных органических удобрений (х, т/га) на уровень урожайности зерновых культур (у, ц/га) по 10 хозяйствам района. Связь между признаками выражается параболой второго порядка. Данные расчетов представим в табл. 9.7

Таблица 9.7.

№ хозяйства	х	у	у2	х2	ху	х3	х4	х2у
1	1	14	196	1	14	1	1	14	13,81	0,19	0,0361
2	2	18	324	4	36	8	16	72	17,52	0,48	0,2304
3	3	20	400	9	60	27	81	180	20,76	-0,76	0,5776
4	4	25	625	16	100	64	256	400	23,52	1,48	2,1904
5	5	23	529	25	115	125	625	575	25,81	-2,81	7,8961
6	6	27	729	36	162	216	1296	972	27,61	-0,61	0,3721
7	7	30	900	49	210	342	2401	1470	28,94	1,06	1,1236
8	8	32	1024	64	256	512	4096	2048	29,79	2,21	4,8841
9	9	30	900	81	270	729	6561	2430	30,17	-0,17	0,0289
10	10	29	841	100	290	1000	10000	2900	30,07	-1,07	1,1449
Итого	55	248	6468	385	1513	3025	25333	11061	248,0	-	18,4842

Подставим данные табл. 9.6. в систему нормальных уравнений:

10а₀+55а₁ +385а₂= 248;

55а₀+ 385а₁+3025а₂= 1513;

385а₀+ 3085а₁+ 25333а₂= 11061.

Преобразуем систему путем деления соответствующих значений на коэффициенты при первых членах. В результате получим: а₀= 9,61; а₁= 4,435; а₂= - 0,239.

Следовательно,

Определим, при каком количестве внесенных органических удобрений, будет достигнута наивысшая урожайность зерновых:

т/га

На основе уравнения параболы второго порядка рассчитано, что при внесении органических удобрений на 1 га посевов в размере 9,3 т наивысшая урожайность зерновых культур достигнет:

= 9,61 + 4,435^.9,3 – 0,239^.9,3²= 30 ц/га.

Вычислим корреляционное отношение:

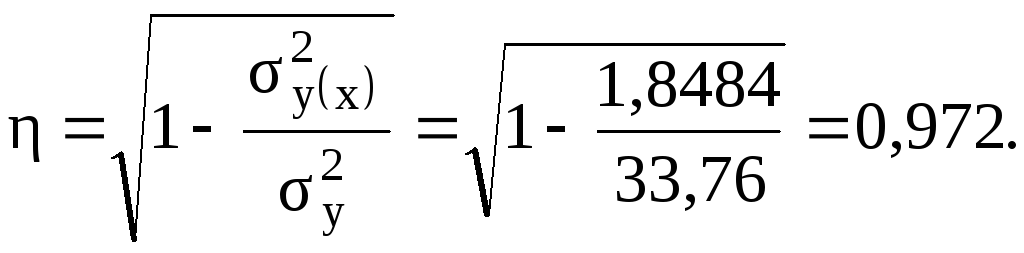
Исчисленный коэффициент корреляционного отношения близок к единице, что свидетельствует о достаточно тесной связи между исследованными признаками.

Зависимость между тремя и более признаками называется множественной или многофакторнойкорреляционной зависимостью. Линейная связь между тремя признаками выражается уравнением:

(9.34)

а система нормальных уравнений для определения параметров а₀, а₁и а₂будет следующей:

(9.35)

Теснота связи между тремя признаками измеряется с помощью множественного (совокупного) коэффициента корреляции:

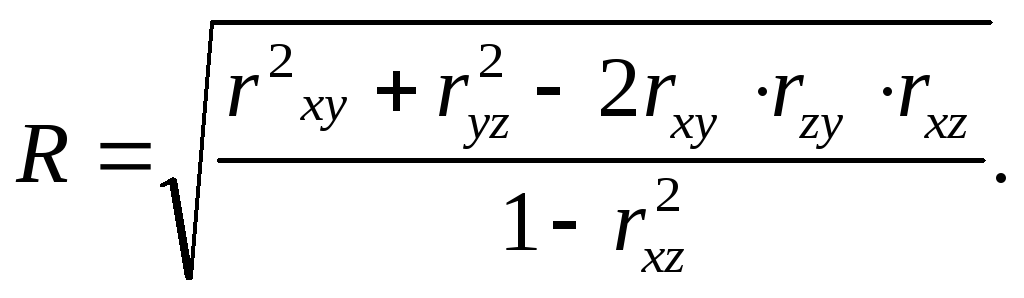, (9.36)

где - парные коэффициенты корреляции.

Наряду с парными коэффициентами вычисляются и частные коэффициенты корреляции. Они характеризуют тесноту связи между парой признаков при условии элиминирования (закрепления на среднем уровне) значений остальных признаков. Применительно к взаимосвязи трех признаков частные коэффициенты корреляции исчисляются:

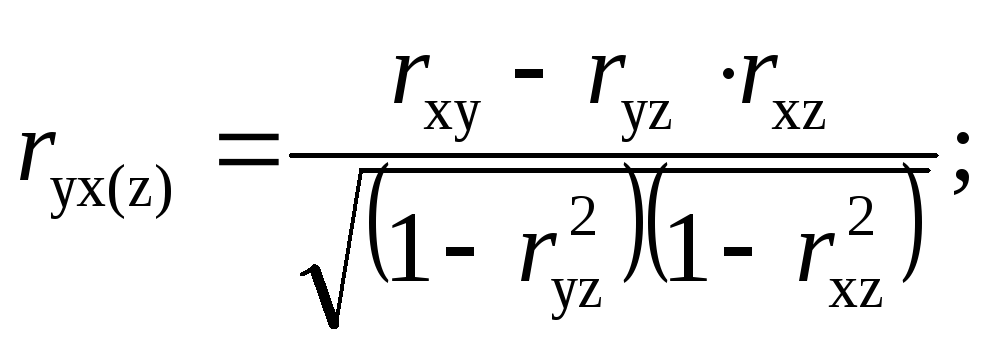(9.37)

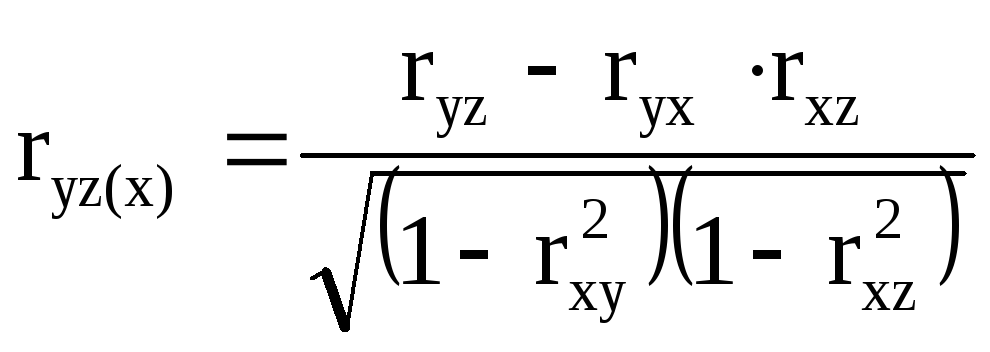. (9.38)

Множественный коэффициент корреляции в квадрате (R²) называется коэффициентом детерминации. Он показывает долю вариации результативного признака, обусловленную вариацией факторных признаков, включенную в регрессионную модель.

Пример 7. Определим зависимость между уровнями урожайности зерновых культур (y, ц/га) и двумя факторами: размером внесения минеральных удобрений (х, ц/га) и сроками уборки (z, дней). Результаты подсчета приведем в табл. 9.8.

Таблица 9.8

№ фермы	у	x	z	х2	xy	у2	z2	yz	xz
1	14	1	9	1	14	196	81	126	9	15,10
2	18	3	8	9	54	324	64	144	24	20,11
3	20	2	8	4	40	400	64	160	16	18,70
4	23	2	7	4	46	529	49	161	14	20,89
5	26	4	6	16	104	676	36	156	24	25,90
6	24	4	7	16	96	576	49	168	28	23,71
7	28	5	6	25	140	784	36	168	30	27,31
8	27	5	5	25	135	729	25	135	25	25,90
9	29	6	6	36	174	841	36	174	36	28,72
10	30	7	6	49	217	961	36	186	42	30,13
Итого	240	39	68	185	1020	6016	476	1578	248	240,07

10а₀ + 39а₁ +68а₂=240;

39а₀ + 185а₁ +248а₂=1020;

68а₀ + 248а₁ +476а₂=1578.

Отсюда: а₀ = 33,4; а₁ = 1,41; а₂= - 2,19.

Следовательно, =33,4+1,41х – 2,19z.

Значение парных коэффициентов корреляции по данным табл. 9.8 составят:

r_yx = 0,915; r_yz = - 0,915; r_xz = - 0,813.

Множественный коэффициент корреляции равен:

Вычислим множественный коэффициент детерминации: R²=(0,961)²= 0,924, или 92,4%, то есть вариация урожайности зерновых культур на 92,4% обусловлена вариацией двух факторных признаков, включенных в регрессионную модель (размером внесения минеральных удобрений и сроками уборки урожая).

Рассчитаем частные коэффициенты корреляции:

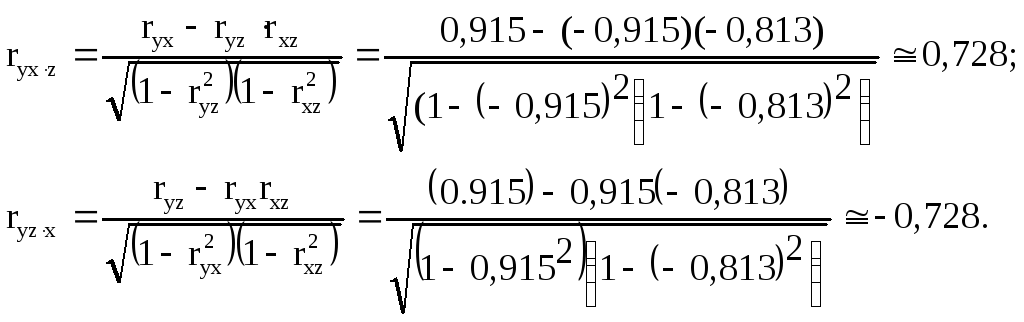
Частные коэффициенты корреляции оказались меньше, чем парные. Это связано с тем, что сопутствующее влияние одного из факторов в каждом из частных коэффициентов корреляции элиминировано.

Для многофакторных регрессионных моделей с числом факторов больше двух целесообразно множественный коэффициент корреляции исчислять по формуле:

, (9.39)

где r₁₂, r_{13, …,} r_1p – парные коэффициенты корреляции между результативным и каждым из факторных признаков, включенных в регрессионную модель:

- бетта-коэффициенты – это коэффициенты регрессии в стандартизованном масштабе, показывающие, на какую величину среднеквадратического отклонения (сигмы) изменится результативный признак, если каждый из факторных признаков увеличится на одну сигму. Бетта-коэффициенты рассчитываются:

, (9.40)

где a_j – коэффициенты регрессии при каждом из признаков – факторов;

σ₁ - среднеквадратическое отклонение результативного признака;

σ_j - среднеквадратические отклонения по каждому из факторных признаков.

Множественный коэффициент детерминации вычисляется по формуле:

(9.41)

В приведенной формуле каждое из выражений, входящих в сумму значений, показывает долю вариации результативного признака, обусловленную вариацией каждого из факторов регрессионной модели.

Пример 8. Линейные коэффициенты корреляции между уровнем результативного признака и тремя его факторами составляли: 0,60; 0,75; и 0,68, а - коэффициенты соответственно: 0,30; 0,46 и 0,50.