
Дымков Лекции
.pdf
© БГЭУ Лекция №3 Основы теории вероятностей проф. Дымков М. П. 7
Из интегральной теоремы Лапласа можно получить формулу
m |
|
|
|
n |
|
|
|
|
ε |
|
. |
||||
P |
n |
− p < ε |
≈ Φ |
|
|
||
|
|
|
|
pq |
|
||
Пример. Вероятность появления события в каждом из независимых испытаний равна 0,5. Найти число испытаний n, при котором с вероятностью 0,7698 можно ожидать, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.
Решение. |
|
По условию p = 0,5, q = 0,5, ε = 0,02 ; |
||||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|||||
P |
|
|
|
− 0,5 |
≤ 0,02 |
= 0,7698. |
||
n |
||||||||
|
|
|
|
|
|
|
||
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
ε |
n |
: |
|||
Воспользуемся формулой P |
n |
− p ≤ ε |
≈ Φ |
|
||||||
|
|
|
|
|
|
|
|
pq |
|
|
|
|
n |
|
= 0,7698 |
|
0,04 |
n = |
1,2 |
|
|
|
Φ 0,02 |
|
|
. |
||||||
|
|
0,5 0,5 |
|
|
|
|
|
|
|
|
|
n = 30 |
|
n = 900 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
Ответ: |
n = 900 |
|
|
|
|
|
|
|
|

© БГЭУ Лекция №4 |
Случайные величины |
проф. Дымков М. П. |
1 |
7
Случайной называют величину, которая в результате испытания примет одно и только одно из возможных значений, наперед неизвестное и зависящее от случайных причин, которые заранее нельзя учесть.
Случайные величины (СВ) обозначают буквами Х, У, Z, а их возможные значения – х, у, z…..
Дискретная случайная величина
Дискретной называют случайную величину, которая принимает отдельные, изолированные друг от друга значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным.
Как охарактеризовать СВ?
Дискретная случайная величина может быть задана рядом распределения – это соответствие между возможными значениями и их вероятностями:
|
Х |
x1 |
x2 |
|
… |
|
|
xn |
|
|
Р |
p1 |
p2 |
|
… |
|
|
pn |
|
|
|
pi = P(X = xi ), i = |
|
. |
|||||
|
|
1,n |
|||||||
События X = x1, X = x2 , K, |
X n = xn |
образуют полную |
|||||||
группу, следовательно, сумма вероятностей этих событий равна единице: p1 + p2 + p3 +Kpn =1.
© БГЭУ Лекция №4 |
Случайные величины |
проф. Дымков М. П. |
2 |
Дискретная случайная величина может быть задана
функцией распределения.
Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х
вероятность того, что случайная величина Х примет |
|
значение меньшее х: |
F(x)= P(X < x) |
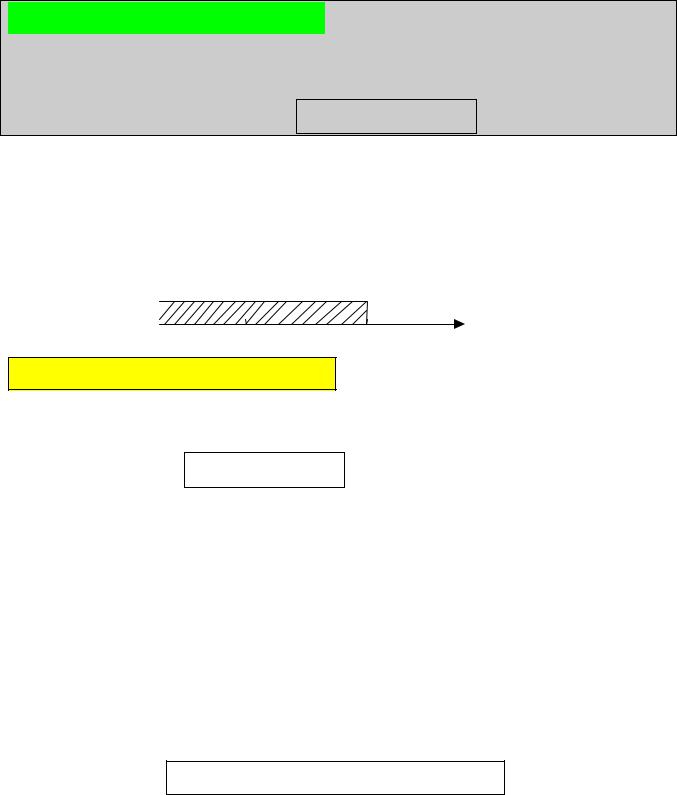
Если значения случайной величины – точки на числовой оси, то геометрически функция распределения интерпретируется как вероятность того, что случайная величина Х попадает левее заданной точки х:
Х< x
0 х х
F (x) обладает свойствами:
1. Функция распределения случайной величины есть
неотрицательная функция, заключенная между нулем и |
|
единицей: |
0 ≤ F(x)≤1. |
2.Функция распределения есть неубывающая функция на всей числовой оси.
3.На минус бесконечности функция распределения
равна нулю, на плюс бесконечности равна 1, т.е. |
|||
|
F(−∞)= lim F(x)= 0, |
F(+∞)= lim F(x)=1 |
. |
|
x→−∞ |
x→+∞ |
|
4. Вероятность попадания случайной величины в интервал [x1, x2 ) (включая x1) равна приращению ее
функции распределения на этом интервале, т.е.
P(x1 ≤ X < x2 )= F(x2 )− F(x1 ).

© БГЭУ Лекция №4 |
Случайные величины |
проф. Дымков М. П. |
3 |
Числовые характеристики случайной величины
Математическое ожидание М (Х)
Пусть случайная величина Х может принимать только значения x1, x2 ,K, xn , вероятности которых
соответственно равны p1, p2 ,K, pn .
Тогда математическое ожидание М (Х) случайной величины Х определяется равенством
n
M (X )= x1 p1 + x2 p2 +K+ xn pn = ∑xi pi .
i=1
Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.
Свойства математического ожидания
1.Математическое ожидание постоянной величины равно самой постоянной: M (C)= C .
2.Постоянный множитель можно выносить за знак математического ожидания: M (CX )=CM (X ).
3.Математическое ожидание алгебраической суммы конечного числа случайных величин равно
алгебраической сумме их математических ожиданий:
M (X ±Y )= M (X )± M (Y ).
4.Математическое ожидание произведения конечного числа независимых случайных величин равно
произведению их математических ожиданий:
M (XY )= M (X )M (Y ).
5.Математическое ожидание отклонения случайной
величины от ее математического ожидания равно нулю: M (X − M (X ))= 0 .
© БГЭУ Лекция №4 |
Случайные величины |
проф. Дымков М. П. |
4 |
Дисперсия случайной величины
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения.
Дисперсией D(X ) случайной величины Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания: D(X )= M [X −M (X )]2 .
Дисперсия – это мера рассеяния случайной величины около ее математического ожидания.
Если Х – дискретная случайная величина, то дисперсию вычисляют по следующим формулам:
n
D(X )= ∑(xi − a)2 pi , (где а = М(Х));
i=1
или
D(X )= M (X 2 )−(M (X ))2 .
Свойства дисперсии случайной величины
1.Дисперсия постоянной величины есть нулю: D(C)= 0 .
2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX )= C 2 D(X ).
3.Дисперсия суммы двух независимых случайных
величин равна сумме дисперсий этих величин:
D(X +Y )= D(X )+ D(Y ).
4.Дисперсия разности двух независимых случайных
величин равна сумме их дисперсий:
D(X −Y )= D(X )+ D(Y ).
© БГЭУ Лекция №4 Случайные величины проф. Дымков М. П. 5
Средним квадратическим отклонением σ случайной
величины Х называется арифметическое значение корня квадратного из ее дисперсии: σ = D(X ).
Биномиальный закон распределения
Если вероятность появления события А в каждом испытании постоянна и равна р, то число появлений события А – дискретная случайная величина Х,
принимающая значения 0,1,2,…,m, K, n с вероятностями
Pn (m)= Cnm pmqn−m , 0 < p <1, q =1 − p, m = 0, 1, K, n.
Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, вычисляется по формулам: M (X )= np , D(X )= npq .
Распределение Пуассона
Дискретная величина X имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, K, m,....
(счетное множество значений) с вероятностями
P (X = m)= λme−λ ,
n |
m! |
||
|
|||
Числовые характеристики равны |
|
. |
|
M (X )= D(X )= λ |
|||
Непрерывные случайные величины. Плотность вероятности
Функцией распределения случайной величины Х называется функция F (х), выражающая для каждого х
вероятность того, что случайная величина Х примет |
|
значение, меньшее х: |
F(x)= P(X < x). |
© БГЭУ Лекция №4 |
Случайные величины |
проф. Дымков М. П. |
6 |
Случайная величина Х называется непрерывной, если ее
функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
Примеры непрерывных случайных величин: диаметр детали, которую токарь обтачивает до заданного размера, рост человека, дальность полета снаряда и др.
Теорема. Вероятность любого отдельно взятого
значения непрерывной случайной величины равна нулю:
P(X = x1 )= 0.
Следствие. Если Х – непрерывная случайная величина, то вероятность попадания случайной величины в интервал (x1, x2 ) не зависит от того, является этот
интервал открытым или закрытым, т.е.
P(x1 < X < x2 )= P(x1 ≤ X < x2 )= P(x1 < X ≤ x2 )= P(x1 ≤ X ≤ x2 )
Для непрерывной случайной величины
P(x1 < X < x2 )= F(x2 )− F(x1 ).
Задание непрерывной случайной величины с помощью функции распределения не является единственным.
Плотностью вероятности (плотностью распределения
или просто плотностью) р (х) непрерывной случайной величины Х называется производная ее функции распределения: p(x)= F′(x).
Плотность вероятности р(х), как и функция распределения F(х), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин.
© БГЭУ Лекция №4 |
Случайные величины |
проф. Дымков М. П. |
7 |
Свойства плотности вероятности непрерывной случайной величины:
1.p(x)≥ 0;
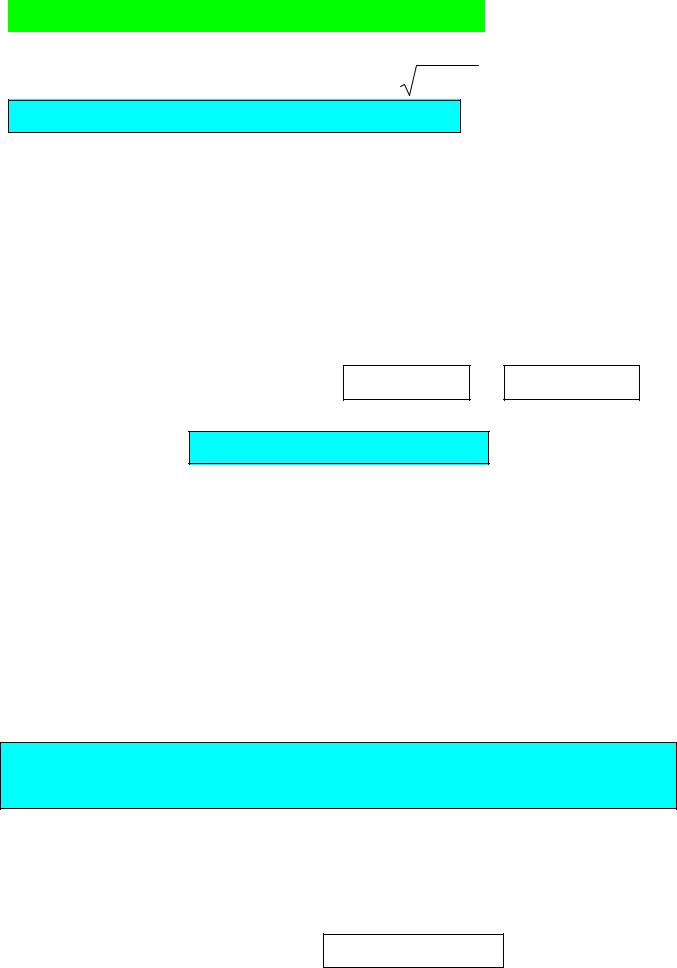
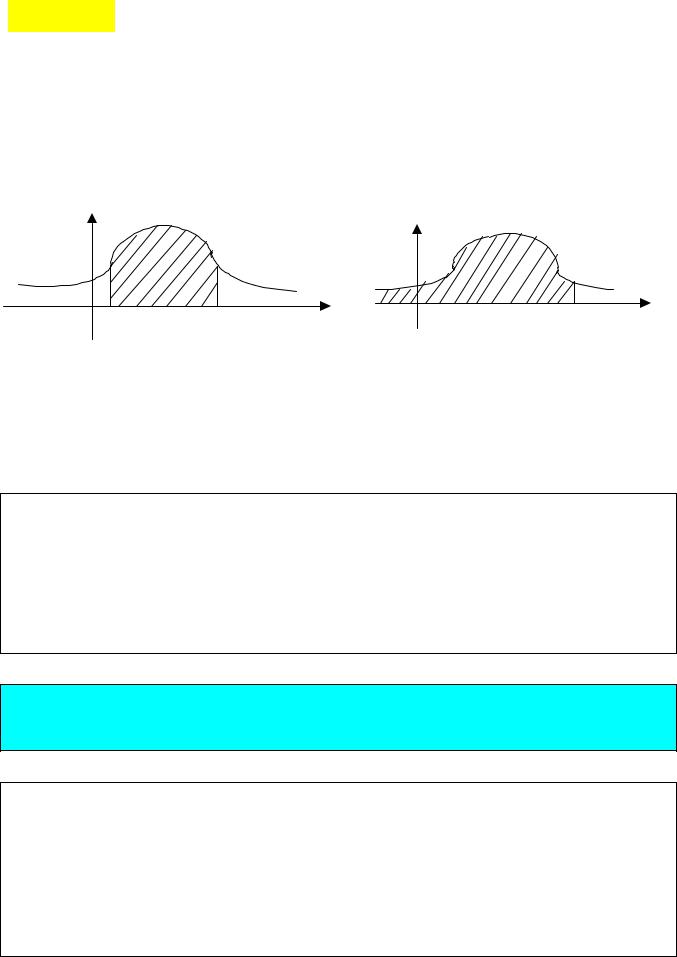
2.P(a ≤ X ≤b)= b∫ p(x)dx, (рис. 1);
a
р(х) |
|
|
|
Р(а≤Х≤ b) |
|
а |
b |
х |
3. F(x)= x∫ p(x)dx, (рис. 2);
−∞
+∞
4.∫ p(x)dx =1.
−∞
р(х) |
|
F(х) |
|
х |
х |
Геометрически свойства плотности вероятности означают, что ее график – кривая распределения – лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
Числовые характеристики непрерывных случайных величин
Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат
|
M (X )= |
+∞ |
всей оси Ох, есть величина |
∫xp(x)dx |
|
|
|
−∞ |
где р(х) – плотность распределения случайной величины.
© БГЭУ Лекция №4 |
Случайные величины |
проф. Дымков М. П. |
8 |
Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат
интервалу |
( |
) |
, то |
M (X )= b xp(x)dx |
. |
|
a b; |
∫ |
|||
|
|
|
|
a |
|
Дисперсия непрерывной случайной величины Х, возможные значения которые принадлежат всей оси Ох,
определяется равенством D(X )= +∫∞[x −M (X )]2 p(x)dx,
−∞
или равносильным равенством
D(X )= +∫∞ x2 p(x)dx −[M (X )]2 .
−∞
Вчастности, если все возможные значения Х
принадлежат (a b;), то D(X )= b∫[x −M (X )]2 p(x)dx,
|
a |
или |
D(X )= b∫x2 p(x)dx −[M (X )]2 . |
|
a |
Все свойства математического ожидания и дисперсии для дискретных случайных величин справедливы и для непрерывных величин.
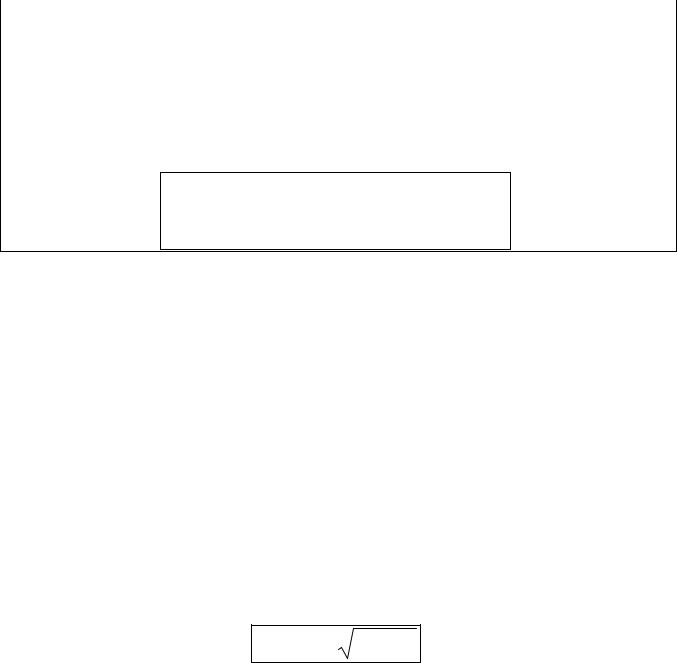
Среднее квадратическое отклонение непрерывной
случайной величины определяется равенством:
σ(X )= D(X ).
Модой M0 (X ) непрерывной случайной величины Х
называется ее наиболее вероятное значение (для которого плотность вероятности р(х) достигает максимума).
© БГЭУ Лекция №4 |
Случайные величины |
проф. Дымков М. П. |
9 |
||||
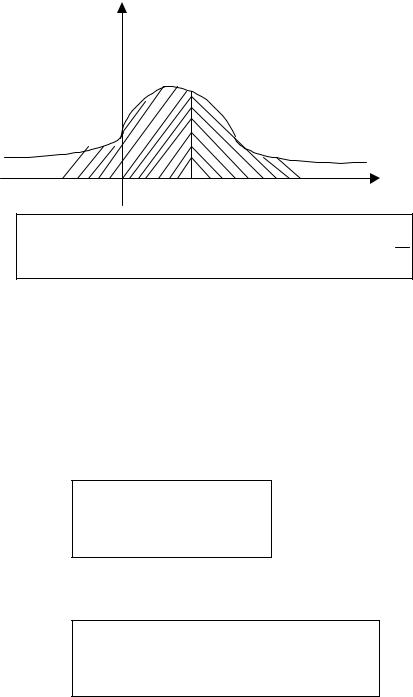
Медианой Me (X ) непрерывной случайной величины Х |
|||||||
называется такое ее значение, для которого |
|
|
|||||
|
р(х) |
|
|
|
|
|
|
|
|
Р1=1/2 |
|
|
|
|
|
|
|
|
Р2=1/2 |
|
|
|
|
|
|
Ме(Х) |
|
х |
|
|
|
P(X < Me (X ))= P(X > Me (X ))= |
1 . |
|
|||||
|
|
|
|
|
|
2 |
|
Геометрически, |
вертикальная |
прямая |
x = Me (X ), |
||||
проходящая через точку с абсциссой, равной Me (X ), |
|||||||
делит площадь фигуры под кривой распределения на две |
|||||||
равные части (рис. ). Очевидно, что F(M e (X ))=1/ 2. |
|
||||||
Начальный теоретический момент порядка k |
|||||||
непрерывной |
случайной |
величины |
Х |
определяется |
|||
|
νk |
+∞ |
|
|
|
|
|
равенством |
= ∫ xk p(x)dx . |
|
|
|
|
||
|
|
−∞ |
|
|
|
|
|
Центральный теоретический момент порядка k |
|||||||
непрерывной случайной величины Х определяется |
|||||||
равенством |
µk |
= +∫∞[x −M (X )]k p(x)dx. |
|
|
|||
|
|
−∞ |
|
|
|
|
|
Если все возможные значения Х принадлежат интервалу |
|||||||
(a b;), то νk = b∫xk p(x)dx, µk = b∫[x −M (X )]k p(x)dx.
a |
a |
