БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.Н |
|
|
3) |
Уравнение прямой, проходящей через две точки: |
|||||||
|
x − 0 |
= |
y + 4 |
; |
x |
= |
y + 4 |
; |
4x = −3y −12; |
4x + 3y +12 = 0 |
|
−3 − 0 |
0 + 4 |
|
4 |
||||||
|
|
|
−3 |
|
x2 + y2 + 4x − 6 y −3 = 0 есть уравнение окружности. |
|||||
Пример 2. Показать, |
что |
|
||||||||
Найти ее центр и радиус.
Решение. Выделим полные квадраты для переменной x и y . x2 + y2 + 4x − 6 y −3 = 0
(x2 + 4x + 4) + ( y2 −6 y +9) − 4 −9 −3 = 0 (x + 2)2 + ( y −3)2 −16 = 0
(x + 2)2 + ( y −3)2 =16
Уравнение окружности имеет вид (6.13), центр окружности находится в точке A(−2,3) , радиус равен 4.
Гипербола
Гиперболой называется геометрическое место точек на плоскости, для которых разность расстояний до двух данных точек, называемых фокусами есть величина постоянная.
y |
|
|
b |
|
M(x, y) |
F1 |
a F2 |
x |
c |
|
|
По определению |
|
F1M − F2M = 2a , |
(6.14) |
где сумму расстояний точек гиперболы от фокусов обозначили через 2a . F1, F2
– фокусы гиперболы. Расстояние между фокусами F1F2 = 2c . Из треугольника F1MF2 :
|
|
F1M |
|
− |
|
F2M |
|
< |
|
F1F2 |
|
|
, откуда следует соотношение: |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
a < c |
(6.15) |
||||||
Выберем на гиперболе произвольную точку М(х, у). Тогда: |
|||||||||||||
|
F M = (x + c)2 + y2 |
F M = (x − c)2 + y2 |
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
2 |
||
(x + c)2 + y2 − (x − c)2 + y2 = 2a
(x + c)2 + y2 = 4a2 + 4a (x − c)2 + y2 + (x − c)2 + y2
59
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.Н |
4a (x − c)2 + y2 = −4a2 + 4xc |
|
a2 (x − c)2 + a2 y2 = a4 − 2a2 xc + x2 c2 |
|
a2 x2 |
− 2a2 xc + a2 c2 + a2 y2 = a4 − 2a2 xc + x2 c2 |
a2 x2 |
+ a2 c2 + a2 y2 − a4 − x2 c2 = 0 |
− x2 (c2 − a2 ) + a2 (c2 − a2 ) + a2 y2 = 0 |
|
x2 (c2 − a2 ) − a2 y2 = a2 (c2 − a2 ) |
|
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось) a2b2 = b2 x2 − a2 y2
|
x2 |
− |
y2 |
=1 |
(6.16) |
|
|
|
|||
|
a2 |
b2 |
|
||
Получили каноническое уравнение гиперболы. |
|
||||
Гипербола симметрична относительно начала координат и относительно |
|||||
осей координат. |
|
||||
Ось 2a называется действительной осью гиперболы. |
|
||||
Ось 2b называется мнимой осью гиперболы. |
его основной |
||||
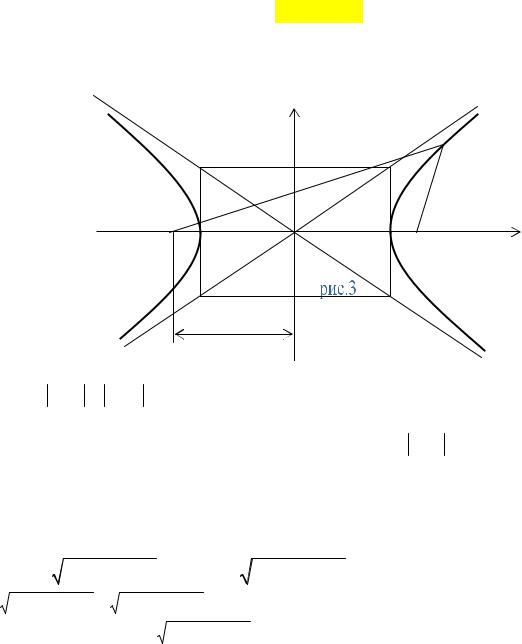
Для |
построения гиперболы удобно использовать |
||||
прямоугольник–прямоугольник со сторонами 2a и 2b , стороны которого проходят через вершины гиперболы симметрично относительно координатных
осей. |
Прямые |
y = ± b x , |
проходящие через |
противоположные вершины |
||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
основного прямоугольника, являются асимптотами гиперболы. |
||||||||||||||
|
|
|
Гипербола целиком находится вне основного прямоугольника, касаясь |
|||||||||||
его сторон в своих вершинах. |
|
|
||||||||||||
|
|
|
Отношение ε = |
c |
>1называется эксцентриситетом гиперболы, где c – |
|||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
половина расстояния между фокусами, a – действительная полуось. |
||||||||||||||
|
|
|
С учетом того, что с2–а2=b2: |
|
||||||||||
ε |
2 |
= |
c2 |
= |
a2 |
+b2 |
=1 |
+ |
b2 |
|
|
|
||
|
a2 |
|
a2 |
a2 |
|
|
|
|||||||
b |
|
|
|
|
|
|
|
|
||||||
= ε2 −1 |
|
|
|
|
|
|
|
|
|
|||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
a = b , |
|
|
ε = |
2 , |
то гипербола |
называется равнобочной |
||||
(равносторонней). Чем ближе ε |
к 1, тем теснее прижата гипербола к оси Ox . |
|||||||||||||
При ε →1 гипербола вырождается в два луча (−∞, −a] и [a, +∞) ; при ε → +∞ – в пару прямых, параллельных оси Oy .
Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии εa от него,
называются директрисами гиперболы. Их уравнения: x = ±εa .
60