Аналитическая геометрия

Лекция 5

Предмет аналитической геометрии

Аналитическая геометрия–раздел геометрии, в котором простейшие геометрические образы (прямые, плоскости, линии и поверхности второго порядка) исследуются средствами алгебры на основе метода координат . В данном разделе будет использована декартова прямоугольная система координат, определенная в лекции 4. В дальнейшем нами будет изучена также полярная система координат.

В аналитической геометрии на плоскости решается общая задача, состоящая в исследовании формы, расположения и свойств данной линии. Пусть мы имеем некоторую линию на плоскости. Координаты x и y точки,

лежащие на этой линии, не могут быть произвольными; они должны быть подчинены известным ограничениям, обусловленным геометрическими свойствами данной линии. Тот факт, что числа x и y являются координатами

точки, лежащей на данной линии, аналитически записывается в виде некоторого уравнения. Это уравнение называется уравнением линии на плоскости.

Сущность метода координат на плоскости заключается в том, что всякой линии сопоставляется ее уравнение, а затем свойства этой линии изучаются путем аналитического исследования соответствующего уравнения. Введем основное понятие аналитической геометрии.

Уравнением линии на плоскости называется уравнение F(x, y) = 0 ,

которому удовлетворяют координаты любой точки данной линии и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Займемся систематическим изучением линий по их уравнениям и в первую очередь рассмотрим прямую линию на плоскости.

Прямая линия на плоскости

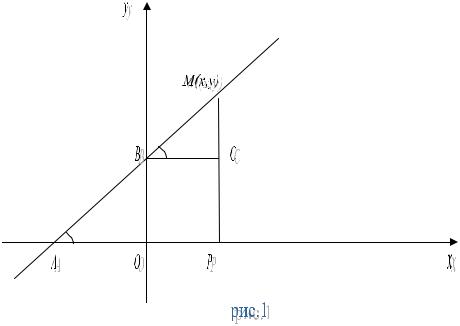
Выведем уравнение прямой AB, заданной величинами b и k = tgϕ , где угол ϕ образован данной прямой с положительным направлением оси Ox .

Для этого возьмем на прямой AB произвольную точку M (x, y) и опустим

метод координат был предложен в 17 веке французскими математиками П.Ферма (1601–1665) и Р. Декартом (1596–1650)

44

Этому уравнению удовлетворяют координаты x, y каждой точки M ,

лежащей на данной прямой. Обратно, легко убедиться, что если координаты какой-либо точки связаны уравнением (5.4), то эта точка лежит на прямой AB. Следовательно, (5.4) и есть уравнение прямой AB. Уравнение (5.4) носит название уравнения прямой с угловым коэффициентом. Входящие в него величины b и k , определяющие положение прямой на плоскости, называют параметрами этой прямой. Оба эти параметра могут быть любыми действительными числами.

Отметим, что текущие координаты x и y входят в уравнение (5.4) прямой в первой степени, поэтому будем говорить, что прямая есть линия

45

Уравнение (5.7) получается как частный случай из уравнения (5.4) при k = tg0 = 0 .

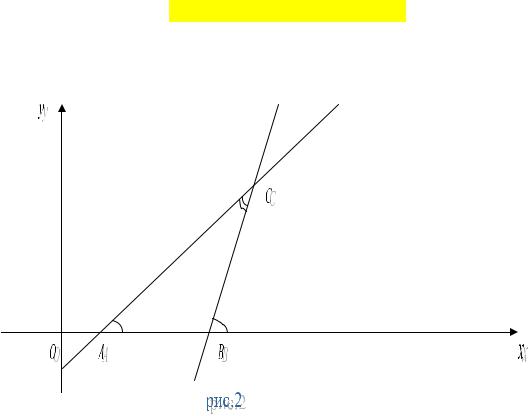
Угол между двумя прямыми

Рассмотрим две прямые (не параллельные оси Oy ), заданные их уравнениями с угловыми коэффициентами (рис.2)

Для параллельности двух прямых необходимо и достаточно, чтобы имело место равенство

Для перпендикулярности двух прямых необходимо и достаточно, чтобы имело место равенство

Пример 1. Определить острый угол между прямыми y=-3x+7; y=2x+1. Решение. k1=-3; k2=2

Пример 2. Показать, что прямые 3х–5у+7=0 и 10х+6у–3=0 перпендикулярны. Решение. k1=3/5, k2=-5/3, k1k2=-1, следовательно, прямые перпендикулярны.

46

Уравнения прямой, проходящей через данную точку в данном направлении

Пусть прямая PM наклонена под углом ϕ к положительному направлению оси Ox и проходит через заданную точку P(x1, y1) .

Выведем уравнение этой прямой, предполагая сначала, что прямая не параллельна оси Oy . В этом случае, как мы видели, уравнение прямой имеет

вид (5.4). Так как точка P(x1, y1) лежит на прямой PM , то координаты x1, y1 должны удовлетворять уравнению (5.4): y1 = kx1 +b . Вычитая данное равенство из равенства (5.4), получаем:

Если прямая, проходящая через заданную точку P(x1, y1) , параллельна оси Oy ,

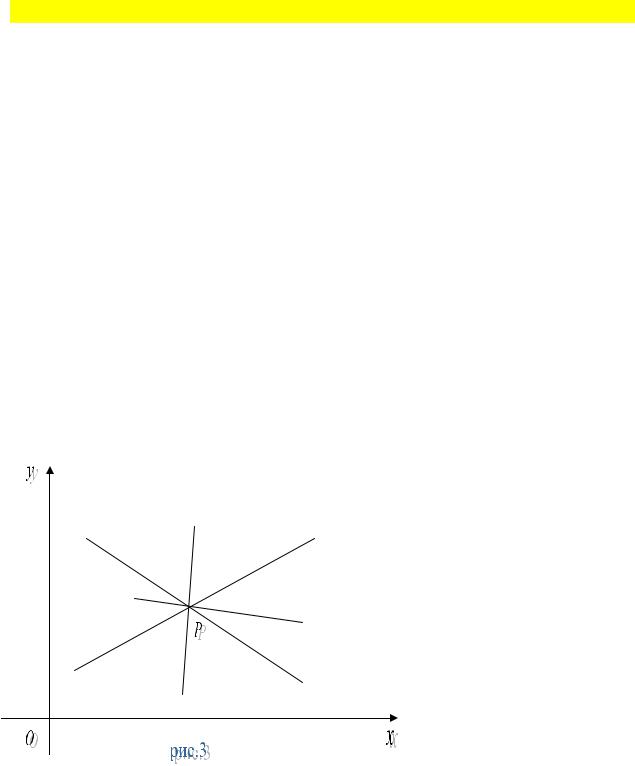
Если k –заданное число, то уравнение (5.13) представляет вполне определенную прямую, если же k –переменный параметр, то это уравнение определит пучок прямых, проходящих через точку P(x1, y1) (рис.3), при этом

k называется параметром пучка.

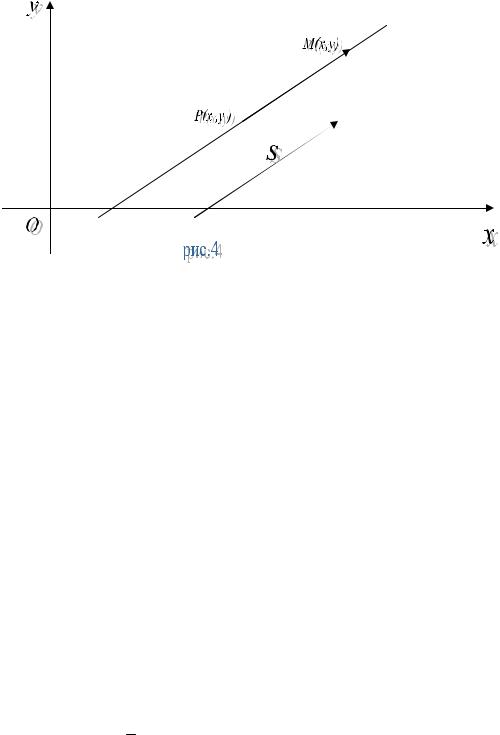
НаправлениеG прямой PM можно также задать с помощью направляющего вектора s ={p,q}, параллельного данной прямой (рис.4).

47

некоторому числу t , которое назовем параметром, то получим так называемое

параметрическое уравнение прямой:

Отметим, что параметрическое и каноническое уравнения прямой можно записать не единственным образом (вместо точки P(x1, y1) можно взять какую-

либо другую точку, вместо вектора s ={p,q}можно взять любой вектор,

параллельный ему).

Пример 3. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

2x–3y+3=0; y = 23 x +1.

Искомое уравнение высоты имеет вид: y − y1 = k(x − x1) или с учетом того, что она опущена из вершины C(12; -1): y −12 = k(x +1) . Коэффициент k определим

из условия 23 k = −1 или k = − 32 .

48