
- •Линейная алгебра
- •Лекция 2
- •Лекция 3
- •Лекция 4
- •Аналитическая геометрия
- •Лекция 5
- •Уравнения прямой, проходящей через две данные точки
- •Уравнения прямой в отрезках
- •Совместное исследование уравнений двух прямых
- •Расстояние от точки до прямой
- •Лекция 6
- •По определению
- •Из очевидных геометрических соотношений можно записать:
- •Лекция 7
- •Составим уравнение плоскости, проходящей через данные точки
- •Уравнение линии в пространстве
- •Уравнения прямой в пространстве
- •Угол между прямыми в пространстве
- •Условия параллельности и перпендикулярности
- •Понятие гиперплоскости, выпуклого множества
- •Лекция 8
- •Собственные значения и собственные векторы
- •Введение в математический анализ
- •Операции над множествами
- •Отображения (функции)
- •Способы задания функций
- •Виды функций
- •Обратная функция
- •Лекция 10
- •Монотонные последовательности
- •Число е
- •Лекция 11
- •Свойства эквивалентных бесконечно малых
- •Лекция 12
- •Лекция 13
- •Непрерывность функции на интервале и на отрезке
- •Дифференциальное исчисление функции
- •Лекция 15
- •Общие правила нахождения высших производных
- •Лекция 16
- •Исследование функций и построение графиков
- •Исследование функции на экстремум с помощью
- •Выпуклость и вогнутость кривой.
- •Лекция 18
- •Рис. 1. Два члена разложения
- •Рис. 2. Четыре члена разложения
- •Рис. 3. Шесть членов разложения
- •Теоретические вопросы к экзамену

БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
|
Лекция 4 |
Вектора на плоскости и в пространстве
Вматематике и ее приложениях различают два типа величин: скалярные
ивекторные. Скалярная величина полностью определяется одним числом, которое выражает отношение данной величины к соответствующей единице измерения, например, масса тела, температура, объем, работа.
Векторными величинами, или векторами, называют те, которые характеризуются не только их числовым значением, но и направлением в
пространстве \3 или на плоскости \2 , например, сила, скорость, ускорение. Для изучения общих свойств, присущих всем векторным величинам, в
математике вводят понятие абстрактного математического вектора, в котором сохранено лишь то общее, что имеют все физические векторы: величина и направление.
Естественным изображением математического вектора (упорядоченная пара точек) служит направленный отрезок: длина отрезка равна числовому значению (модулю) вектора, а направление отрезка, указываемое стрелкой,
совпадает с направлением этого вектора. Обозначается вектор АВ, а; модуль вектора обозначается АВ, а .
Будем рассматривать свободные векторы, которые определяются длиной и направлением и точка приложения которых может быть выбрана произвольно.
Вектор, начало и конец которого совпадают (в силу этого он не имеет определенного направления), называется нуль-вектором или нулевым
вектором. Обозначается нулевой вектор 0 .
Вектор, длина которого равна единице, называется единичным вектором.
Векторы называются ортогональными, если они лежатG на перпендикулярных прямых. Обозначаются ортогональные векторы aG b .
Векторы называются коллинеарными, если они лежат на одной прямой
или параллельных прямых. Обозначаются коллинеарные |
вектора |
aG|| b . |
|
Коллинеарные векторы могут быть сонаправленными |
G |
G |
или |
a |
↑↑ b |
||
противоположно направленными aG ↑↓ b . Нулевой вектор коллинеарен любому вектору.
Два ненулевых вектора a и b называются равными, если они имеют одинаковые модули и направление: aG = b .
Два коллинеарных вектора a и b называются противоположнымиG , если
они имеют одинаковые модули и противоположное направление: aG = −b . Векторы, лежащие в параллельных плоскостях (или в одной плоскости)
называются компланарными.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
34
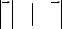
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
|
|
|
Линейные операции над векторами |
|
|
Как было сказано в лекции 3, линейными операциями над векторами |
|||
называется их сложение и умножение на число. |
||||
cG |
Суммой двух геометрических векторов a и b называется третий вектор |
|||
, начало которого совпадает с началом вектора a , а конец – с концом вектора |
||||
bG |
при условии, что вектор bGотложен из конца вектора a . Записывают cG = aG + b . |
|||
Вектор cG |
можно построить по правилу треугольника или по правилу |
|||
параллелограмма. Сумма нескольких векторов может быть найдена по правилу многоугольника.
Произведением вектора a на число α называется вектор b =α aG, удовлетворяющий условиям
1. b = α
 a
a
2. вектор aG сонаправлен с вектором b ( a ↑↑b ), если α > 0;
вектор aG противоположно направлен с вектором b ( a ↑↓b ), если α < 0.
Из определения коллинеарности векторов и операции умножения вектора на число вытекает
Утверждение 1. Векторы a и b коллинеарны тогда и только тогда, |
|||
G |
G |
G |
G |
когда b |
=αa |
или a |
= βb . |
Теорема 1. Для того чтобы любые два вектора были линейно зависимы необходимо и достаточно, чтобы они были коллинеарны.
Доказательство теоремы непосредственно вытекает из определения линейнойG G зависимостиG и утверждения 1:
aG|| b b =αaG aG и b –линейно зависимы.
Теорема 2. Для того чтобы любые три вектора были линейно зависимы
необходимо и достаточно, чтобы они были компланарными. |
|
||||||
Теорема 3. Если |
G |
G |
линейно независимые векторы, то любой вектор |
||||
a |
и b |
||||||
cG, компланарный с |
ними, |
можно единственным образом представить |
в |
||||
G |
G |
G |
Такое представление называется разложением вектора c |
по |
|||
виде: c |
= xa + yb . |
||||||
|
G |
G |
x и y |
– коэффициенты разложения. |
|
||
векторам a |
и b ; |
|
|||||
Из теоремы 3 следует, что все векторы, лежащие в некоторой плоскости, можно рассматривать как линейные комбинации каких-либо двух неколлинеарных (линейно независимых) векторов на этой плоскости. Аналогичный результат справедлив и для пространственных векторов.
Теорема 4. Если три вектора aG, b и c линейно независимы
(некомпланарныG ), тоGлюбой векторG d пространства \3 можно разложить по векторам aG, b и cG: d = xaG+ yb + zcG и такое представление единственно.
35

БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
Из теоремы 4 следует, что все векторы пространства\3 можно рассматривать как линейные комбинации каких-либо трех некомпланарных (линейно независимых) векторов.
|
пространстве\3 |
|
Векторный базис |
|
e1, eG2 , eG3 |
|
|
|
Пусть в |
|
заданы три вектора |
и пусть |
d |
– |
|||
произвольный вектор пространства. Будем говорить, что векторы e1, eG2 , eG3 |
||||||||
образуют в пространстве векторный базис, если |
любой |
вектор |
d |
в |
||||
пространстве |
представим в |
виде d = xeG1 + yeG2 + zeG3 |
и это |
представление |
||||
единственно.
Коэффициенты x, y, z разложения называются координатами (компонентами) вектора dG в базисе e1, eG2 , eG3 . Записывают d ={x, y, z}.
Из теоремы 4 следует, что три любых некомпланарных вектора, взятые в определенном порядке, образуют в пространстве векторный базис.
Если векторы, образующие базис, единичны и попарно ортогональны, то
базис называется ортонормированным. Ортонормированный базис будем
обозначать iG, Gj, kG : iG = Gj = kG =1 , i Gj, Gj k , kG iG .
Замечание. Если рассматривать векторы, лежащие в какой-либо плоскости, то по теореме 3 векторный базис на плоскости образуют любые два неколлинеарные векторы eG1, eG2 , лежащие в этой плоскости.
Базисом на прямой является любой ненулевой вектор. |
|
||||||
Пример 1. Даны векторыaG |
(1; 2; 3), |
b (-1; 0; 3), |
с (2; 1; -1) и |
d (3; 2; 2) в |
|||
некотором базисе. Показать, что векторы a , |
b и |
с образуют базис и найти |
|||||
координаты вектора d |
в этом базисе. |
|
|
|
|
||
G |
G |
G |
образуют |
базис, |
если |
они линейно |
независимы, |
Решение. Векторы a |
, b |
, с |
|||||
другими словами, если существует нетривиальное (ненулевое) решение системы уравнений:
α − β + 2γ = 0
2α + 0 β +γ = 0 , которая является следствием векторного равенства:
3α + 3β −γ = 0
1 |
−1 |
2 |
0 |
||
α 2 |
+ β 0 |
|
+γ 1 |
|
= 0 . |
3 |
3 |
|
−1 |
0 |
|
Это условие выполняется, если определитель матрицы системы отличен от нуля.
1 −1 2
20 1 ≠ 0
33 −1
36

БГЭУ 2006 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лекции по высшей математике для студентов I курса |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
||||||||
|
|
1 |
−1 |
2 |
|
|
= |
|
0 |
|
1 |
|
+ |
|
2 |
1 |
|
+ 2 |
|
2 |
0 |
|
= −3 + (−2 −3) +12 = 4 ≠ 0 . |
Таким |
образом, |
|||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
3 |
3 |
−1 |
|
|
|
|
1 |
|
−1 |
|
|
|
3 |
−1 |
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
G |
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
G |
G |
G |
G |
|
|
||||
|
|
|
|
G |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
векторы a |
, b |
с |
образуют базис и d |
= xa + yb |
+ zc . |
|
|
|||||||||||||||||||||
|
|
|
1 |
−1 |
|
2 |
|
3 |
|
|
|
|
x − y + 2z = 3 |
|
|
|||||||||||||
|
x 2 + y 0 |
|
+ z 1 |
|
|
= 2 |
|
или |
2x + 0 y + z = 2 |
|
|
|||||||||||||||||
|
|
|
3 |
3 |
|
−1 2 |
|
|
|
|
3x +3y − z = 2 |
|
|
|||||||||||||||
Для решения этой системы воспользуемся методом Крамера.
∆1 = |
|
d1 |
b1 |
c1 |
|
|
|
|
|
|
|
3 |
−1 |
2 |
|
|
|
0 1 |
|
2 1 |
|
|
2 0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
d2 |
b2 |
c2 |
|
|
= |
|
2 0 |
1 |
|
|
= 3 |
+ |
+ |
2 |
= 3(−3) + (−2 − 2) +12 = −1. |
|||||||||||||||
|
|
|
d3 |
b3 |
c3 |
|
|
|
|
|
|
|
2 |
3 |
−1 |
|
|
|
3 −1 |
|
2 −1 |
|
|
2 3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x = |
∆1 = −1/ 4 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∆2 = |
|
a1 |
d1 |
c1 |
|
|
|
|
|
|
|
1 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
a2 |
d2 |
c2 |
|
|
|
|
= |
|
|
2 |
2 |
1 |
|
= (−2 − 2) −3(−2 −3) + 2(4 − 6) = −4 +15 − 4 = 7; |
||||||||||||||||
|
|
|
a3 |
d3 |
c3 |
|
|
|
|
|
|
|
3 |
2 −1 |
|
|
|
|
|
|
|
|
|
|
|||||||
y = |
∆2 |
= 7 / 4; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a1 |
b1 |
d1 |
|
|
|
|
1 |
−1 |
3 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
∆3= |
a2 |
b2 |
d2 |
|
|
= |
|
2 |
0 |
2 |
= −6 + (4 −6) +18 =10; |
||||||||||||||||||||
|
a3 |
b3 |
d3 |
|
|
|
|
3 |
3 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||
z = |
∆3 = 5/ 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Координаты вектора d |
в базисе a , b , с : |
d |
={-1/4, 7/4, 5/2}. |
||||||||||||||||||||||||||||
Как следует из примера 1, процедура нахождения координат вектора в произвольном базисе достаточно трудоемка и связана с решением СЛАУ.
Система координат
Для определения положения произвольной точки могут использоваться различные системы координат. Положение произвольной точки в какойлибо системе координат должно однозначно определяться. Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса. Как на плоскости, так и в пространстве возможно задание самых разнообразных систем координат. Выбор системы координат зависит от характера поставленной геометрической, физической или технической задачи. Рассмотрим некоторые наиболее часто применяемые на практике системы координат.
37

БГЭУ 2006 |
|
лекции по высшей математике для студентов I курса |
|||
|
|
|
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
||
|
Декартова прямоугольная система координат в пространстве. |
|
|||
Аффинная |
|
Координаты вектора, точки |
задается точкой О |
||
система координат в пространстве |
|||||
(началом координат) и упорядоченной тройкой приложенных к ней некомпланарных векторов eG1, eG2 , eG3 (базисных векторов).
Декартова прямоугольная система координат (как частный случай аффинной системы координат) называется ортонормированной и правой, если в качестве базиса рассматривать орты i , Gj, k при условии, что эти векторы образуют правую тройку.
Тройка некомпланарных упорядоченных векторов aG, b и cG , приведенных к общему началу, называется правой, если кратчайший поворот от aG к b виден из конца вектора cG против хода часовой стрелки, в противном случае (когда поворот наблюдается по ходу часовой стрелки) тройка векторов называется
левой.
При круговой перестановкеG векторов ориентация тройки не изменяется, например, все тройки ( aG, b , cG), ( c , aG, b ), ( b , c , a )–правые. При перестановке
двух векторов ориентация тройки изменится на противоположную, например, |
||||
G G |
G |
G |
G |
G |
( a, b |
, c )–правая тройка, (b |
, a , c )–левая. Ортонормированный базис |
i , j, k |
|
образует правую тройку. |
|
|
||
|
Прямые, проходящие через начало координат в направлении базисных |
|||
векторов |
iG, Gj, kG, называются осями координат: Ox – ось абсцисс; Oy – ось |
|||
ординат; Oz – ось аппликат. Плоскости, проходящие через пару осей координат, называются координатными плоскостями: плоскость Oxy, плоскость Oxz, плоскость Oyz. Прямоугольная декартова система координат в пространствеG G обозначаетсяG Оxyz. Кроме направления базисные вектора
i ={1,0,0}, j ={0,1,0},k ={0,0,1} задают соответственно и единицу масштаба по
каждой оси Ox, Oy, Oz.
Зафиксируем в пространстве точку O(0,0,0) и рассмотрим произвольную
точку М. Вектор ОМ назовем радиус-вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую упорядоченную тройку чисел – компоненты ее радиус-вектора.
Прямоугольными декартовыми координатами точки М в системе
координат Оxyz называются коэффициенты разложения вектора ОМ по базису |
||
(iG, |
Gj,kG) : |
|
|
OM = xiG + yjG + zk |
(4.1) |
Записывают M (x, y, z) .
Чтобы найти компоненты вектора нужно из координат его конца вычесть
координаты начала. Радиус-вектор точки М имеет те же координаты, что и |
||||||
точка M : OMG |
={x, y, z}. |
|
||||
Если заданы точки A(x1, y1, z1) и B(x2 , y2 , z2 ) , то |
|
|||||
ABG ={x |
− x , y |
2 |
− y , z |
2 |
− z } |
(4.2) |
2 |
1 |
1 |
1 |
|
||
38

БГЭУ 2006 |
|
лекции по высшей математике для студентов I курса |
G |
G |
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
G |
Действительно, AB = OB −OA.
Длина произвольного вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две
точкиA(x1, y1, z1) и B(x2 , y2 , z2 ) в пространстве \3 , то длина вектора AB , как следует из формулы (3.9), вычисляется по формуле
AB = (x2 − x1 )2 + ( y2 − y1 )2 + (z2 − z1 )2 |
(4.3) |
Если точка М(х, у, z) делит отрезок АВ в соотношении
то координаты этой точки определяются как:
x = |
µx1 + λx2 |
; |
y = |
µy1 + λy2 |
; |
z = |
µz1 + λz2 . |
|
µ + λ |
|
|
µ + λ |
|
|
µ + λ |
λ/µ, считая от А,
(4.4)
В частном случае координаты середины отрезка находятся как:
x = |
x1 + x2 |
; |
y = |
y1 + y2 |
; |
z = |
z1 + z2 |
. |
(4.5) |
|
|
|
|||||||
2 |
|
2 |
|
2 |
|
|
|||
Линейные операции над векторами в координатах, как следует из (3.5), (3.6)
имеютGвидG: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
a ± b = (xa ± xb ; ya ± yb ; za ± zb ); α a |
= (αxa ;α ya ;αza ) |
|
|
|
|||||||||||||||||||||||||||||||
|
|
В лекции 3 были определены скалярное произведение и угол между |
|||||||||||||||||||||||||||||||||||
векторами формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
G |
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b = xa xb + ya yb + za zb; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
G |
G |
x x + y y + z z |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
cosϕ = |
a b |
2 |
2 |
|
|
|
|
|
(4.6) |
||||||||||||||||||||||
|
|
|
|
|
|
G |
G = |
2 |
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
|
a |
|
b |
|
|
a b |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
xa + ya + za |
|
xb + yb + zb |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Скалярное произведение ненулевых векторов a и b |
равно нулю тогда и |
||||||||||||||||||||||||||||||||||
только тогда, когда они ортогональны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
G |
G |
b ), если |
|
G |
= 2, |
|
b |
|
= 3, |
G |
|
|
|
||||||||||||
Найти (5 a + 3 b )(2 a - |
|
a |
|
|
a b. |
|
|
||||||||||||||||||||||||||||||
Решение. |
|
G |
|
|
G |
|
|
|
G G |
|
G |
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
G G |
|
G |
|
G |
|
|
|
= 10 |
2 |
−3 |
|
2 |
= 40 − 27 =13 , |
|
|
|
|
|||||||||||||||||||
10 a a |
- 5 a |
b + 6 a |
b |
- 3 b b |
a |
|
b |
|
|
|
|
|
|
||||||||||||||||||||||||
|
G |
G |
= |
G |
2 |
|
|
G |
G |
= |
G |
2 |
|
G |
|
G |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
т.к. a |
a |
a |
|
= 4, b |
b |
b |
|
= 9, a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
G |
G |
||||||||||||||
Пример |
|
3. |
|
|
Найти |
угол |
между |
|
векторами |
|
a и |
b , |
если |
||||||||||||||||||||||||
G |
G |
|
|
a |
= i + 2 j + 3k , |
||||||||||||||||||||||||||||||||
G |
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b |
= 6i + 4 j |
− 2k . |
|
|
|
|
G |
|
|
|
aG = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. aG=(1, 2, 3), |
|
|
|
1 + 4 +9 = |
14, |
b = |
36 +16 + 4 = 56 |
||||||||||||||||||||||||||||||
b =(6, 4, -2), |
|
||||||||||||||||||||||||||||||||||||
aG bG = 6 + 8 – 6 = 8.
cosϕ = |
|
8 |
= |
2 |
8 |
= |
4 |
= |
2 |
; |
ϕ = arccos |
2 . |
|
||
|
|
|
14 |
56 |
14 |
14 |
14 |
|
7 |
|
|
7 |
G |
||
Пример |
|
4. |
Найти |
скалярное |
|
произведение |
(3 a - 2 b ) (5 aG |
||||||||
|
|
- 6b ), если |
|||||||||||||
|
G |
|
G |
|
G |
G |
= π / 3. |
|
|
|
|
|
|
|
|
|
a |
= 4, b |
= 6, а^ b |
|
|
|
|
|
|
|
|||||
Решение. 15 aG aG-18 a bG -10 aG bG +12 b b =15 aG 2 − 28 aG
 bG cos π3 +12 bG 2 =
bG cos π3 +12 bG 2 =
39

БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
=15 16 − 28 4 6 1 |
+12 36=240–336+432=672–336=336. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
G |
|
|
Пример 5. Найти угол между векторами a и b , если aG = 3i + |
|
|
||||||||||||||||||||||||
4 j |
+ 5k , |
|
|
|||||||||||||||||||||||
bG |
= 4iG + 5 Gj −3kG . |
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
=(4, 5, -3), a b =12 + 20-15 =17, |
|
|
|
|
|
|
|||||||||
Решение. aG=(3, 4, 5), b |
|
|
|
|
|
|
||||||||||||||||||||
aG |
= 9 +16 + 25 = |
50; |
|
bG |
= |
16 + 25 + 9 = |
50 . |
|
|
|
|
|
|
|
||||||||||||
cosϕ = |
17 |
|
|
= |
17 ; |
|
|
ϕ = arccos 17 . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
50 |
50 |
|
50 |
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|||
Пример 6. При каком m векторы aG = mi + j и b = 3i −3 j − 4k |
перпендикулярны. |
|||||||||||||||||||||||||
Решение. aG |
= (m, 1, 0); |
|
G |
= (3, -3, -4) |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
||||||||||||||||
G |
G |
|
= 0; m =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
a |
b = 3m −3 |
|
|
|
|
|
|
|
|
2aG + 3b + 4cG |
|
5aG + 6b + 7cG, |
||||||||||||||
Пример 7. Найти скалярное произведение векторов |
и |
|||||||||||||||||||||||||
если |
G |
|
=1, |
|
G |
|
= 2, |
G |
|
3, |
G |
G |
G |
G |
G G |
π |
|
|
|
|
|
|
|
|||
a |
|
|
b |
|
c |
= |
a^ b |
= a^ c |
= b ^ c |
= 3 . |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
G |
|
|
G |
|
G |
G |
|
G |
G |
|
G G |
G G |
|
G |
G |
G G |
G |
||||
|
|
|
|
|
+ |
|
|
|
G |
|
||||||||||||||||
Решение.( 2a |
3b |
+ 4c )(5a + 6b + 7c )=10a |
a |
+12a |
b +14a c |
+15a |
b |
+18b |
b |
+ 21b c + |
||||||||||||||||
+ |
G G |
|
G |
G |
|
G |
G |
|
G G |
G |
b + |
G G |
G |
|
|
|
G G |
|
|
|||||||
20c a |
+ 24b |
c |
+ 28c |
c =10 a |
a + 27a |
34a c + |
45b c +18b b |
+ 28c c = 10 + |
||||||||||||||||||
+ 27 + 51 + 135 + 72 + 252 = 547.
Векторным |
|
Векторное произведение векторов |
|
||||||||||||
|
произведением ненулевых векторов |
|
|||||||||||||
вектор cG |
|
, удовлетворяющий следующим условиям: |
|||||||||||||
1) |
|
cG |
|
= |
|
aG |
|
|
|
b |
|
sinϕ , где ϕ - угол между векторами a и b , |
|||
|
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
|
sinϕ ≥ 0; |
0 ≤ ϕ ≤ π |
||||||||||||
2)векторG cGортогонален векторам a и b
3)aG, b и cG образуютG правую тройку векторов. Обозначается: cG = aG×b илиcG = [aG,b]
G
a и b называется
cG G
b
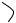 ϕ
ϕ
aG
Свойства векторного произведения векторов:
1)векторноеG произведениеG не коммутативно: b ×aG = −aG×b ;
2)aG×b = 0G aG bGили aG= 0 Gили b = 0;
3)(m aGG)×b = aG×(mbG ) = m( aG×b );
4)aG×(b + сG ) = aG×b + aG× сG ;
5)Если заданы векторы aG(xa, ya, za) и b (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами i , j, k , то
40

БГЭУ 2006 |
|
|
|
|
лекции по высшей математике для студентов I курса |
||||
|
|
|
iG |
Gj |
|
|
|
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
|
G |
G |
= |
k |
|
|
|
|
||
a |
×b |
xa |
ya |
za |
|
|
|
|
|
|
|
|
xb |
yb |
zb |
|
|
|
|
6) |
Геометрический смысл векторного произведения: |
длина вектора |
|||||||
G |
G |
(модуль |
векторного |
|
произведения) равна площади |
параллелограмма, |
|||
a |
×b |
G |
|||||||
построенного на векторах |
G |
|
|||||||
a |
и b . |
|
|||||||
Пример 8. Найти векторное произведение векторов aG = 2i + 5 j + k и b = i + 2 j −3k . |
||||||||||||||||||||||||||||||||||||||||||
Решение. aG = (2, 5, 1); |
|
|
|
bG = (1, 2, -3) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
iG Gj |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
G |
G |
|
G |
|
5 1 |
|
|
|
|
|
|
G |
|
2 1 |
|
|
|
G |
|
2 5 |
|
|
|
|
G |
G |
|
G |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
a ×b = |
2 5 1 |
= i |
|
2 −3 |
− j |
|
1 −3 |
+ k |
|
1 2 |
= −17i |
+ 7 j − k . |
|
|
||||||||||||||||||||||||||||
|
|
1 |
2 |
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 9. Вычислить площадь треугольника с вершинами А(2, 2, 2), |
|
|||||||||||||||||||||||||||||||||||||||||
В(4, 0, 3), С(0, 1, 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
JJJG |
|
|
|
|
|||||||||||||||
|
|
|
JJJG |
|
|
|
2;1− 2;0 − 2) = (−2;−1;−2); |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Решение. AC = (0 − |
|
|
AB = (4 − 2;0 − 2;3 − 2) = (2;−2;1) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
G |
|
G |
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
i |
|
j |
k |
|
|
G |
|
|
|
−1 − 2 |
|
|
|
G |
|
− 2 − 2 |
|
G |
|
− 2 −1 |
|
G |
G |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
AC × AB = |
− 2 −1 − 2 |
= i |
|
− 2 1 |
|
|
− j |
|
2 |
1 |
|
+ k |
|
2 − 2 |
|
= i (−1 − 4) |
− j(−2 + 4) + |
|||||||||||||||||||||||||
G |
|
|
|
|
2 |
− 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
G |
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(4 + 2) |
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
+ k |
= −5i − |
2 j + |
6k. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
AC × AB = |
25 + 4 + 36 = |
65. |
|
|
|
|
|
|
|
|
|
|
S∆ = |
|
|
65 (ед2). |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
cG = i − j + k |
Пример 10. |
Доказать, |
|
что векторы aG = 7i −3 j + 2k , |
|
b = 3i − 7 j +8k и |
|||||||||||||||||||||||||||||||||||||
компланарны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 −1 1 1 −1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3 |
− 7 |
|
8 |
~ |
0 |
− 4 |
|
|
|
|
|
5 , т.к. векторы линейно зависимы, то они компланарны. |
||||||||||||||||||||||||||||||
7 −3 2 |
|
0 4 −5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Пример |
11. |
Найти площадь |
параллелограмма, построенного на |
векторах |
||||||||||||||||||||||||||||||||||||||
aG + 3b; |
3aG + b , если |
|
aG |
|
= |
|
b |
|
=1; aG^ b = 300. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение.
(aG + 3b) ×(3aG +b) = 3aG×aG + aG×b +9b ×aG + 3b ×b = −b ×aG + 9b ×aG = 8b ×aG
S = 8 b 
 aG sin 300 = 4 (ед2).
aG sin 300 = 4 (ед2).
Смешанное произведение векторов
Смешанным (векторно-скалярным) произведением векторов aG, b и c
называется число, равное скалярному произведению вектора aG на вектор, равный векторному произведениюG векторов b и c .
Обозначается aG b ×cG или ( a , b , c ).
41
БГЭУ 2006 |
|
|
лекции по высшей математике для студентов I курса |
||||||||||||
|
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
||||||||||||||
|
Свойства смешанного произведения |
|
|
|
|
|
|
|
|||||||
1)при циклической (круговой) |
перестановке |
множителей |
смешанное |
||||||||||||
|
G |
G |
G G G |
G G |
G |
|
|
|
|
|
|
|
|
||
произведение не изменяется (a,b,c) = (b,c,a) |
= (c,a,b) |
|
|
|
|
|
|
|
|
||||||
2)при перестановке двух сомножителей смешанное произведение меняет |
|||||||||||||||
|
G G |
G |
|
G |
G G |
G G |
G |
G G |
G |
|
|
|
|
||
знак на противоположный (a,b,c ) |
= −(b |
,a,c ); (a,b |
,c )= −(a,c |
,b ) |
|
|
|
|
|||||||
3) (λaG1 + µaG2 ,b, cG) = λ(aG1 ,b, cG) + µ(aG2 ,b, cG) |
|
|
|
|
|
|
|
|
|
|
|||||
G |
G |
, y2 |
, z2 ), |
|
G |
|
|
G G |
G |
|
x1 |
y1 |
z1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
= |
x2 |
y2 |
z2 |
|
|
|||||||
4)Если a |
= (x1, y1, z1) , b = (x2 |
|
c = (x3 |
, y3 , z3 ) , то (a,b |
, c) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
x3 |
y3 |
z3 |
|
|
5)Смешанное произведение равно нулю тогда и только тогда, если: а) хоть один из векторов равен нулю; б) два из векторов коллинеарны; в) векторы компланарны.
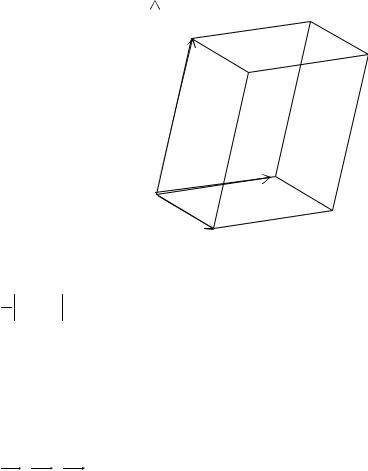
6)ГеометрическийG смысл смешанного произведения: смешанное произведение aGG b ×cG по модулю равно объему параллелепипеда, построенного
на векторах aG, b Gи c .
b ×cG
aG
cG
G b
Объем треугольной пирамиды, образованной векторами aG, bG и cG, равен
16 (aG,bG, cG)
Пример 12. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), |
|
||||||||||||||||||||
D(1; 5; 0) лежат в одной плоскости. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. |
|
|
|
|
Найдем |
JJJG |
координаты |
векторов: |
|||||||||||||
JJJG |
−6;1); |
JJJG |
|
|
|
|
|
|
|
|
|||||||||||
AB = (−2; |
AC = (4; |
−3;−2); AD = (−4;−2;2) |
|
||||||||||||||||||
Найдем смешанное произведение полученных векторов: |
|
||||||||||||||||||||
AB AC AD = |
|
− 2 |
− 6 |
1 |
|
|
|
|
− 2 − 6 1 |
|
|
|
0 − 6 |
1 |
|
= 0 , |
|
||||
|
|
|
|
|
|
|
|||||||||||||||
|
4 −3 |
− 2 |
|
= |
|
0 |
−15 |
0 |
|
= |
|
0 |
−15 |
0 |
|
|
|||||
|
|
|
− 4 |
− 2 |
2 |
|
|
|
|
0 |
10 |
0 |
|
|
|
0 |
10 |
0 |
|
|
|
42
БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
ст. преподавателя, кандидата физ.-мат. наук Поддубной О.H |
Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
Пример 13. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3),
D(3; 7; 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. |
|
|
|
JJJG |
Найдем |
JJJG |
координаты |
векторов: |
|||||||||
JJJG |
= (−2; |
−3;−4); |
|
−3); |
= (4;−1;−2) |
|
|
|
|
||||||||
BA |
BD = (1;4; |
BC |
|
|
|
|
|||||||||||
Объем пирамиды |
|
|
|
|
|
|
|
|
|
|
|
||||||
V = |
1 |
|
−2 |
−3 |
−4 |
|
= |
1 |
(−2(−8 |
−3) |
+3(−2 +12) −4(−1−16)) |
= |
1 |
3 |
) |
||
|
|
||||||||||||||||
6 |
|
1 |
4 |
−3 |
|
6 |
6 |
(22 +30 +68) = 20(ед |
|||||||||
|
|
4 |
−1 |
−2 |
|
|
|
|
|
|
|
|
|
|
|||
Для нахождения длины высоты пирамиды найдем сначала площадь основания
BCD.
|
|
iG |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
BD × BC = |
|
j |
|
|
|
|
G |
|
G |
G |
G |
G |
G |
||||
1 |
4 |
|
−3 |
= i (−8 |
−3) − j(−2 +12) + k (−1 −16) = −11i |
−10 j |
−17k. |
||||||||||
|
|
4 |
−1 |
− 2 |
|
|
|
|
|
|
|
|
|
||||
BD × BC = |
112 |
|
+102 |
+172 = |
121 +100 + 289 = |
510 |
|
|
|||||||||
Sосн = 510 / 2 (ед2) |
|
|
|
|
|
|
|
|
|
|
|||||||
Т.к. V = |
Sосн h |
|
; |
|
h = |
|
3V |
= |
120 |
= 4 510 |
(ед). |
|
|
||||
|
|
|
3 |
|
|
|
|
|
|
|
Sосн |
510 |
17 |
|
|
|
|
43
