
- •Линейная алгебра
- •Лекция 2
- •Лекция 3
- •Лекция 4
- •Аналитическая геометрия
- •Лекция 5
- •Уравнения прямой, проходящей через две данные точки
- •Уравнения прямой в отрезках
- •Совместное исследование уравнений двух прямых
- •Расстояние от точки до прямой
- •Лекция 6
- •По определению
- •Из очевидных геометрических соотношений можно записать:
- •Лекция 7
- •Составим уравнение плоскости, проходящей через данные точки
- •Уравнение линии в пространстве
- •Уравнения прямой в пространстве
- •Угол между прямыми в пространстве
- •Условия параллельности и перпендикулярности
- •Понятие гиперплоскости, выпуклого множества
- •Лекция 8
- •Собственные значения и собственные векторы
- •Введение в математический анализ
- •Операции над множествами
- •Отображения (функции)
- •Способы задания функций
- •Виды функций
- •Обратная функция
- •Лекция 10
- •Монотонные последовательности
- •Число е
- •Лекция 11
- •Свойства эквивалентных бесконечно малых
- •Лекция 12
- •Лекция 13
- •Непрерывность функции на интервале и на отрезке
- •Дифференциальное исчисление функции
- •Лекция 15
- •Общие правила нахождения высших производных
- •Лекция 16
- •Исследование функций и построение графиков
- •Исследование функции на экстремум с помощью
- •Выпуклость и вогнутость кривой.
- •Лекция 18
- •Рис. 1. Два члена разложения
- •Рис. 2. Четыре члена разложения
- •Рис. 3. Шесть членов разложения
- •Теоретические вопросы к экзамену

БГЭУ 2006 |
лекции по высшей математике для студентов I курса |
|
|
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
|
|
Исследование функций и построение графиков |
|
|
Лекция 17 |
|
Возрастание и убывание функций
Теорема 1. Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f′(x) > 0 (f′(x) < 0) для a<x<b, то эта функция строго возрастает (убывает) на отрезке [a, b].
Доказательство. Пусть f′(x)>0 для любых точек х1 и х2, принадлежащих отрезку [a, b], причем x1<x2. Тогда по теореме Лагранжа: f(x2)–f(x1)=f′(ε)(x2 – x1),
x1<ε <x2. По условию f′(ε)>0, следовательно, |
f(x2)–f(x1) >0, т.е. функция f(x) |
возрастает. Теорема доказана. |
|
Доказанную выше теорему можно проиллюстрировать графически: |
|
y |
y |
ϕ |
ϕ |
ϕ |
ϕ |
|
x |
|
x |
Точки экстремума
Пусть функция f(x) определена в некоторой окрестности точки х0 . Функция f(x) имеет в точке х0 максимум (минимум), если для всех точек х≠ х0 из этой окрестности выполнено неравенство: f(x0) > f(x) (f(x0) < f(x)).
Максимум или минимум функции называется экстремумом функции, а те значения аргумента, при которых достигаются экстремумы функции, называются точками экстремума функции (точки максимума и точки минимума).
Из определения следует, что экстремум функции имеет локальный характер–это наибольшее или наименьшее значение функции по сравнению с ее близлежащими значениями.
Теорема 2. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х0 и точка х0 является точкой экстремума, то в этой точке производная функции равна нулю.
Доказательство. Предположим не ограничивая общности, что функция f(x) имеет в точке х = х0 максимум. Тогда при достаточно малых положительных ∆х>0 верно неравенство:
f (x0 + ∆x) < f (x0 ) , т.е. f (x0 + ∆x) − f (x0 ) < 0
Тогда |
f (x0 + ∆x) − f (x0 ) |
> 0 |
при ∆х< 0 |
|
∆x |
||||
|
|
|
142
БГЭУ 2006
f (x0 + ∆x) − f (x0 ) < 0
∆x
По определению: lim
∆x→0
лекции по высшей математике для студентов I курса ст. преподавателя, к. физ.-мат. н. Поддубной О.H.
при ∆х > 0
f (x0 + ∆x) − f (x0 ) = f ′(x ) .
∆x 0
Т.е. если ∆х→0, но ∆х<0, то f′(х0) ≥ 0, а если ∆х→0, но ∆х>0, то f′(х0) ≤ 0. Возможно это только в том случае, если при ∆х→0 f′(х0) = 0.
Для случая, если функция f(x) имеет в точке х0 минимум теорема доказывается аналогично. Теорема доказана.
Геометрическая интерпретация. Геометрически условие f′(х0) = 0
означает, что в точке экстремума х0 дифференцируемой функции y=f(x) касательная к графику параллельна оси Оx.
Замечание. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум.
Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно.
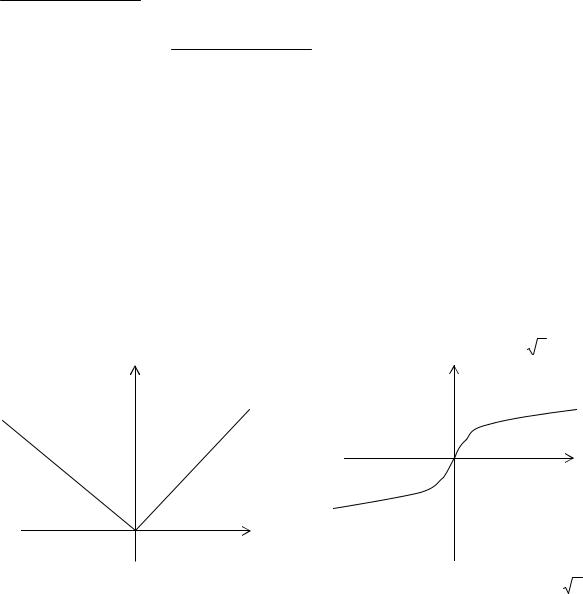
Пример 1. f(x) =|x| |
Пример 2. f(x) = 3 х |
y |
y |
|
x |
|
x |
В точке х = 0 функция f(x) =|x| |
В точке х = 0 функция f(x) = 3 х |
имеет минимум, |
не имеет ни максимума, |
но не имеет производной. |
ни минимума, ни производной. |
Следствие. Непрерывная функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.
Критическими точками функции называются точки из области определения функции, в которых производная функции не существует или равна нулю.
Теорема 3. (Достаточные условия существования экстремума) Пусть функция y=f(x) непрерывна в некоторой окрестности критической точки х0, и дифференцируема во всех точках этой окрестности (кроме, может быть, самой точки х0). Тогда если при переходе через точку х0 слева направо производная функции f′(x) меняет знак с “+” на “-“, то в точке х = х0 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”, то функция имеет в этой точке минимум. ,Если при переходе через точку х0 слева направо производная функции f′(x) не меняет знак, то в точке х0 экстремума нет.
143
БГЭУ 2006 |
|
лекции по высшей математике для студентов I курса |
|||
Доказательство. |
ст. преподавателя, к. физ.-мат. н. Поддубной О.H. |
|
|||
|
|
||||
|
f |
′ |
при |
x < x |
|
|
(x) > 0 |
|
|||
Пусть {f |
′(x) < 0 |
при |
x > x00 |
|
|
По теореме Лагранжа: |
f(x) – f(x0) = f′(ε)(x – x0), где ε – промежуточная точка |
||||
между x и x0. |
|
|
|
||
Тогда: 1) Если х < x0, то ε < x0; f′(ε)>0; f′(ε)(x – x0)<0, следовательно |
f(x) – |
||||
f(x0)<0 |
или f(x) < f(x0). |
|
|
||
f(x0)<0 |
|
2) Если х > x0, то ε > x0 f′(ε)<0; f′(ε)(x – x0)<0, следовательно |
f(x) – |
||
или f(x) < f(x0). |
|
|
|||
Т. к. и в первом и во втором случаях f(x)<f(x0), то можно сказать, что f(x)<f(x0) в любых точках вблизи х0, т.е. х0 – точка максимума.
Доказательство теоремы для точки минимума производится аналогично. Теорема доказана.
Из приведенных теорем 1-3 вытекает следующее правило исследования
функции на экстремум и нахождения промежутков возрастания и убывания функции:
1.Находим область определения функции y = f (x) .
2.находим первую производную функции y = f (x) .
3. приравниваем производную к нулю f ′(x) = 0 и находим все
действительные корни полученного уравнения, а также точки из области определения, в которых производная не существует. Т.о. находим все критические точки функции.
4.на числовой прямой в области определения строим критические точки. Они разобьют область определения на ряд интервалов, в каждом из которых производная сохраняет знак.
5.определяем знак производной в каждом из полученных интервалов (для этого достаточно определить знак производной в какой-нибудь одной
точке каждого из этих интервалов). Если на рассматриваемом интервале f ′(x) > 0 , то это – интервал возрастания, если f ′(x) < 0 , то это–интервал убывания функции.
6.устанавливаем, как меняет знак производная при переходе слева направо через каждую из критических точек. Если при переходе через
критическую точку хi слева направо производная функции f′(x) меняет знак с “+” на “-“, то в точке х = хi функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”, то функция имеет в этой точке минимум.
Приведем алгоритм для нахождения наибольшего и наименьшего
значения (абсолютного максимума и абсолютного минимума) непрерывной на отрезке [a,b] функции y = f (x) :
1)Найти критические точки функции, принадлежащие интервалу (a,b) .
2)Найти значения функции в найденных критических точках.
3)Найти значения функции на концах отрезка.
144
БГЭУ 2006 лекции по высшей математике для студентов I курса ст. преподавателя, к. физ.-мат. н. Поддубной О.H.
4) Выбрать среди полученных значений наибольшее и наименьшее. Пример 3. Найти наибольшее и наименьшее значения функции y = ln2 x − 2ln x
на отрезке [1,5]. |
|
|
|
|
|
Решение. |
Найдем |
|
|
производную |
функции |
y′ = (ln2 x − 2ln x)′ = 2ln x 1 − 2 |
|
1 |
= 2 ln x −1 . |
|
|
|
x |
|
x |
x |
|
Найдем критические точки функции из условий: ln x −1 = 0 или x = 0 . |
|
||||
Т.о. x = e и x = 0 – критически точки исследуемой функции. Однако, отрезку
[1,5] |
принадлежит |
только |
x = e . |
Вычислим значения |
функции |
||||||||||
f (e) = ln2 e − 2ln e =1− 2 = −1 |
|
|
|
|
|
|
|
|
|||||||
f (1) = ln2 1− 2ln1 = 0 − 0 = 0 |
|
|
|
|
|
|
|
|
|||||||
f (5) = ln2 5 − 2ln5 ≈ −0,63 |
|
|
|
|
|
|
|
|
|||||||
Сравнивая |
|
значения |
f (e), |
f (1), f (5) , |
находим |
yнаиб.[1,5] = f (1) = 0 , |
|||||||||
yнаим.[1,5] |
= f (e) = −1. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Исследование функции на экстремум с помощью |
|
|
||||||||||
|
|
|
|
производных высших порядков |
х=х0 имеет максимум, |
||||||||||
Теорема 4. Если f′(x0)=0, то функция f(x) в точке |
|||||||||||||||
если f′′(x0)<0 и минимум, если f′′(x0)>0. |
|
|
|
|
|
|
|||||||||
Доказательство. |
Пусть f′(x0)=0 и f′′(x0)>0. Пусть |
x = x0 + ∆x –точка, |
|||||||||||||
близкая к x0 .Т.к. f′′(x)=(f′(x))′, то имеем |
|
|
|
|
|
|
|||||||||
f ′′(x0 ) = lim |
f ′(x0 + ∆x) − f ′(x0 ) |
= lim |
f ′(x) |
. |
|
|
|
|
|
||||||
|
x − x |
|
|
|
|
|
|||||||||
|
∆x→0 |
|
∆x |
|
x→x0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
f ′(x) |
|
|
|
|
|
|
Таким |
образом, переменная величина |
стремится к |
пределу |
f′′(x0), а |
|||||||||||
x − x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
значит, начиная с некоторого момента эта величина имеет знак своего предела,
т.е. |
f ′(x) |
> 0 при 0 < |
|
x − x |
|
<ε, где ε–достаточно малое положительное число. |
||||||
|
|
|||||||||||
|
||||||||||||
|
x − x0 |
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
f ′(x) |
|
|
|||
Получаем, что числитель и знаменатель дроби |
имеют одинаковые знаки |
|||||||||||
x − x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
и, следовательно, |
|
|
|
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
||||
′ |
− x0 |
< 0 |
|
′ |
|
|
<ε. |
|||||
f (x) < 0 при −ε< x |
|
и f (x) > 0 при 0 < x − x0 |
||||||||||
Производная f ′(x) при переходе через точку x0 меняет свой знак с “-“ на “+”.
На основании теоремы 3 в этой точке функция f(x) имеет минимум. Для случая максимума функции теорема доказывается аналогично.
Если f′′(x0)=0, то характер критической точки x0 неизвестен. Для его определения требуется дальнейшее исследование.
145
