
- •Реферат
- •Summary
- •Содержание
- •Введение
- •1 Система управления запасами: теоретический аспект
- •1.1 Определение, сущность, содержание, классификация запасов
- •1.2 Системы управления запасами, их преимущества и недостатки
- •2 Методы расчета показателей оптимальных партий заказа при многономенклатурных поставках
- •2.1 Методы расчета показателей оптимальных партий заказа при многономенклатурных поставках: теоретический аспект
- •2.2. Многономенклатурные поставки по системе кратных периодов
- •3 Формирование графика многономенклатурных одновременных поставок по товарной линии материалов поставщика в условиях ограничения на грузоподъемность транспортного средства
- •Заключение
- •Список использованных источников
2.2. Многономенклатурные поставки по системе кратных периодов
В
1966 г. профессором Ю. И. Рыжиковым [4] была
предложена стратегия организации
поставок, суть которой сводилась к
объединению преимуществ, свойственных
независимым поставкам с оптимальными
периодичностями
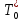 , формула (2.9), и многономенклатурными
поставками с периодичностью Т. Для этого
вводится система кратных периодов,
когда по крайней мере одна номенклатура
заказывается в каждом базисном периоде
Т, а остальные позиции номенклатуры
поставляются с периодичностямиkT
(k
=
1,2,3,...).
, формула (2.9), и многономенклатурными
поставками с периодичностью Т. Для этого
вводится система кратных периодов,
когда по крайней мере одна номенклатура
заказывается в каждом базисном периоде
Т, а остальные позиции номенклатуры
поставляются с периодичностямиkT
(k
=
1,2,3,...).
Рассмотрим простой пример поставки 2 видов продукции.
Допустим, что одна из позиций номенклатуры имеет наименьшую периодичность поставки T = 10 дней. Это означает, что последующие поставки будут производиться с указанной периодичностью и время поставки будет равно 2Т= 20 дней, третьей ЗТ=30 дней и т. д.[1, c.140]
Вторая позиция номенклатуры, поставки которой будут производиться согласно стратегии кратных периодов, имеет периодичность 2Т= 20 дней. Соответственно, вторая поставка будет произведена на 40-й день и т. д. В результате совмещения поставок двух видов продукции получим следующую последовательность: через 10 дней поставляется первый вид продукции, на 20-й день оба вида продукции, на 30-й день - первый вид, на 40-й день – оба вида и т. д.
Согласно [3] оптимальный период группирования определяется по формуле (2.27):

Данному периоду соответствуют минимальные затраты (2.28):

На
основе Т*k
определяются величины поставок S*ik
и количество поставок
 за плановый период (или год).
за плановый период (или год).
Из
формул (2.27), (2.28) следует, что в зависимости
от группировки позиций номенклатуры и
отнесения их к тому или иному кратному
периоду величины
 и
и будут изменяться. Поэтому поиск
конфигурации группировок позиций
номенклатуры представляет собой по
существу итерационный процесс, алгоритм
которого описан в работе [3]. Не вдаваясь
в подробности разработанного алгоритма,
укажем несколько его этапов.
будут изменяться. Поэтому поиск
конфигурации группировок позиций
номенклатуры представляет собой по
существу итерационный процесс, алгоритм
которого описан в работе [3]. Не вдаваясь
в подробности разработанного алгоритма,
укажем несколько его этапов.
1. Позиции
номенклатуры ранжируются по возрастанию
величин показателей D2
Ci/Ai
Cxi.
Нетрудно заметить, что ранжирование
производится фактически с учетом
периодичности независимой поставки
каждой позиции номенклатуры
 .
.
2. Выбираются начальное приближение для кратного периода, за основу принимается первое значение ранжированного ряда (2.29):

3.
Рассчитывается набор коэффициентов
 ,
с помощью которых производится
формирование базового варианта групп
различной кратности.
,
с помощью которых производится
формирование базового варианта групп
различной кратности.
4. Каждая позиция номенклатуры закрепляется за определенной группой.
По
формулам (2.27) и (2.28) для базового варианта
рассчитываются показатели
 и
и и затем с использованием итерационной
процедуры (путем перебора и размещения
позиций номенклатуры в группах различной
кратности) осуществляется поиск
оптимального варианта по критерию
минимума суммарных затрат
и затем с использованием итерационной
процедуры (путем перебора и размещения
позиций номенклатуры в группах различной
кратности) осуществляется поиск
оптимального варианта по критерию
минимума суммарных затрат .
.
Выбор T0 можно осуществить по множеству номенклатур, заказываемых в каждом периоде, при этом первые j позиции номенклатуры из упорядоченного множества заказываются одновременно. Расчетная формула записывается в виде (2.30):

Присоединение к первой группе следующих позиций номенклатуры целесообразно при соблюдении неравенства (2.31):

При подстановке (2.30) в формулу (2.31) условие прекращения накопления группы записывается в виде (2.32):

Проверка
рекуррентного соотношения начинается
со второй позиции номенклатуры, при
этом в правой части подставляются
значения
 и
и .
При выполнении условия (2.32) для всех
последующих позиций i
>
j
вычисляется
оптимальная периодичность
.
При выполнении условия (2.32) для всех
последующих позиций i
>
j
вычисляется
оптимальная периодичность
 и по отношению
и по отношению - начальная кратность.[1,c.143]
- начальная кратность.[1,c.143]
В табл. 2.2 приведены данные о двух видах продукции. Попытаемся ответить на вопрос о целесообразности применения стратегии кратных периодов.
Таблица 2.2 - Исходные данные и результаты расчета при независимой поставке
|
Вид продукции |
Д, ед. |
y.е. |
|
|
y.е. |
дн. |
|
| |||
|
1 |
3000 |
18 |
6 |
1,5 |
465 |
37,7 |
310 |
9,67 (10) | |||
|
2 |
500 |
18 |
6 |
0,5 |
110 |
166 |
227 |
2,2 (2) | |||
|
Сумма |
- |
575 |
- |
12 | |||||||
Примечание – Источник: [1, с.143]
Определим параметры независимых поставок каждого вида продукции (см. табл. 2.2) и совместной поставки:


Поскольку
 >
>
 ,
то объединение в одну поставку
целесообразно.
,
то объединение в одну поставку
целесообразно.
Выполним расчеты периодичности и минимальных суммарных затрат при k = 2 по формулам (2.27) и (2.28):
 .
.

Следовательно, при организации кратных поставок суммарные затраты меньше затрат с независимой, а также совместной (одновременной) поставкой

В табл. 2.3 приведены результаты расчетов T(k) и
 при различных коэффициентах кратности
(см. рис. 2.1, 2.2). Поскольку минимум
суммарных затрат
при различных коэффициентах кратности
(см. рис. 2.1, 2.2). Поскольку минимум
суммарных затрат наблюдается приk
= 2 можно выбрать следующую стратегию
кратных поставок: через каждые 38 дней
поставляется первый вид продукции;
второй вид продукции совместно с первым
- через 76 дней.
наблюдается приk
= 2 можно выбрать следующую стратегию
кратных поставок: через каждые 38 дней
поставляется первый вид продукции;
второй вид продукции совместно с первым
- через 76 дней.
Таблица 2.3 - Результаты расчета параметров поставок при различных коэффициентах кратности
|
Коэффициент
кратности
|
|
|
|
|
|
2 |
27 |
5 000 |
38,9 |
519,6 |
|
3 |
26 |
5 250 |
36,3 |
522,5 |
|
4 |
25,5 |
5 500 |
35,1 |
529,6 |
|
5 |
25,2 |
5 750 |
34,7 |
538,3 |
Примечание – Источник: [1, с.144]
 k
k
Рис.2.1.
Зависимость суммарных затрат
 от коэфф-та кратности
k
от коэфф-та кратности
k
Примечание – Источник: собственная разработка на основе [1, с.144].
 k
k
Рис.2.2. Зависимость периода поставок T(k)от коэффициента кратности k
Примечание – Источник: собственная разработка на основе [1, с.144].
Расчет показателей при двух позициях номенклатуры не вызывает затруднений. Однако при увеличении n количество вариантов возрастает многократно. Проиллюстрируем это с помощью следующего примера.
В табл. 2.4 приведены исходные данные о четырех видах продукции. Требуется выбрать наилучшую стратегию поставок (при С0=18 у.е.).
Таблица 2.4 - Исходные данные и рез-ты расчета при независимых поставках
|
Вид продукции |
|
|
|
у.е |
Si, ед. |
|
|
|
Базовый вариант
| |||
|
1 |
3 000 |
6 |
24 |
1,5 |
310 |
37,7 |
465 |
1 |
1 | |||
|
2 |
2 000 |
4 |
22 |
1,0 |
297 |
54,1 |
297 |
1,43 |
1 | |||
|
3 |
1 000 |
4 |
22 |
0,5 |
210 |
76,6 |
148 |
2,03 |
2 | |||
|
4 |
500 |
6 |
24 |
0,5 |
219 |
160 |
109 |
4,24 |
4 | |||
|
Сумма |
|
1 019 |
|
| ||||||||
Примечание – Источник:[1, с.145].
Для проведения расчетов воспользуемся табл. 2.5, в которой обобщены формулы для трех вариантов многономенклатурных поставок:
- независимые поставки каждой позиции номенклатуры;
- одновременная поставка всех позиции;
- одновременная поставка по системе кратных периодов.[1, c.145]
Таблица 2.5 - Формулы для расчета показателей многономенклат.заказа
|
Наименование показателя |
Независимые поставки |
Одновременно по всей номенклатуре |
Система кратных периодов |
|
Время
выполнения заказа
|
|
|
|
|
Число заказов за период D |
|
|
|
|
Объем
заказа,
|
|
|
|
|
Минимальные
суммарные
затраты
за
период D
|
|
|
|
Примечание:
 ;
; .
.
Примечание – Источник: [1, с.145].
На первом этапе рассчитаем показатели при независимых поставках каждой позиции номенклатуры (см. табл. 2.4).
На втором этапе рассчитаем показатели при одновременной многономенклатурной поставке:
- периодичность поставки

- количество поставок

- минимальные суммарные затраты

- величины поставок каждой позиции номенклатуры, формула (2.10)

На
третьем этапе для предварительно
рассчитанных показателей независимых
поставок (первый этап) проводится их
ранжирование и определяются коэффициенты
кратности
 относительно
приближени T
= 37,7 дня, определенного на первом этапе.
относительно
приближени T
= 37,7 дня, определенного на первом этапе.
На
основании
 выберем базовый вариант кратности
поставок: первый и второй вид продукции
-k
= 1; третий вид - k
= 2; четвертый вид - k
= 4.
выберем базовый вариант кратности
поставок: первый и второй вид продукции
-k
= 1; третий вид - k
= 2; четвертый вид - k
= 4.
Рассчитаем составляющие формул (2.27), (2.28) для базового варианта кратных периодов:


Тогда оптимальный период

минимум суммарных затрат

На
рис. 2.3 приведена диаграмма, отражающая
различные варианты многономенклатурных
поставок, в частности, стратегию кратны:
поставок для базового варианта ( :
1,1,2,4).[1,
с.147]
:
1,1,2,4).[1,
с.147]

Рис. 2.3. Различные варианты многономенклатурных поставок:
а - независимая поставка; б - одновременная поставка; в - кратная поставка, базовый вариант; г- кратная поставка, оптимальный вариант;
о - 1 вид продукции; • - 2 вид продукции; Δ - 3 вид продукции; □ - 4 вид продукции
Примечание – Источник: [1, с.147].
Для расчета величин поставок каждого вида продукции воспользуемся формулой (2.33):

Так, для продукции первого вида находим

Соответственно,
для остальных видов получим
 .
.
В
табл.
2.6
приведены
результаты расчета оптимальных периодов
и минимальных суммарных затрат для
различных стратегий кратных периодов
при многономенклатурных поставках. Из
табл. 2.6 следует, что при организации
поставок в соответствии с пятой стратегией
наблюдается наименьшее значение
минимальных затрат
 =
725 у.е.[1, с.148]
=
725 у.е.[1, с.148]
Таблица 2.6 - Результаты расчета показателей многономенклатурных поставок для различных стратегий
|
Номер стратегии |
Коэффициенты кратности |
y.e. |
y.e. |
дн. |
y.e. | |||||||
|
|
|
|
|
|
|
|
| |||||
|
1 (базовая) |
1 |
1 |
2 |
4 |
31,5 |
8 500 |
31,4 |
732 | ||||
|
2 |
1 |
2 |
2 |
4 |
29,5 |
10 500 |
27.4 |
787 | ||||
|
3 |
1 |
1 |
2 |
2 |
33 |
9 500 |
30,4 |
791 | ||||
|
4 |
1 |
2 |
2 |
2 |
31 |
10 000 |
31,0 |
787 | ||||
|
5 |
1 |
2 |
3 |
4 |
28,8 |
9 000 |
29,2 |
725 | ||||
Примечание – Источник: [1, с.148]
В
табл. 2.7 для пятой стратегии ( :1,2,3,4)
приведены денные о шести поставках за
первое полугодие:
:1,2,3,4)
приведены денные о шести поставках за
первое полугодие:
-
EOQ
каждого
вида продукции ( = 240 ед.,
= 240 ед., = 320 ед.,
= 320 ед., = 240 ед.,
= 240 ед.,
s4 = 160 ед.);
- календарное время каждой поставки;
- виды продукции при каждой поставке (их количество);
- общее кол-во ед-ц поставки с учетом каждого из 4-ех видов продукции.
Таблица 2.7 - Периодичность и объемы многономенклатурных поставок
|
Номер поставки с нач.расч.пер. |
Календарное время, дн. |
Виды продукции при данной поставке |
Общее количество единиц поставки, ед |
|
1 |
29 |
Первый
( |
240 |
|
2 |
58 |
Первый
и второй
( |
560 |
|
3 |
87 |
Первый
и третий
( |
480 |
|
4 |
116 |
Первый,
второй и четвертый
( |
720 |
|
5 |
145 |
Первый |
240 |
|
6 |
174 |
Первый, второй, третий |
800 |
Примечание – Источник: [1, с.148-149]
Соотношение общего количества единиц между первой (240 ед.) и шестой (800 ед.) поставками превышает трехкратную величину, а между первой и двенадцатой поставкой - перепад равен 4. [1,с.149]

 ,
, ,
y.е.
,
y.е. ,
у.е.
,
у.е. ,
, ,
, ,
ед.
,
ед.





 ,
ед.
,
ед. ,
y.е.
,
y.е. ,
у.е.
,
у.е. ,
, ,
дн.
,
дн. ,
у.е.
,
у.е.

 ,
дни
,
дни





















 =240)
=240)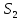 = 320)
= 320) = 240)
= 240) =
160)
=
160)