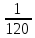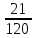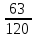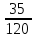Гипергеометрический закон распределения

Возможные значения X: 0,1,…,n. И каждому значению X=m соответствует вероятность P(X=m)=P=.Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N, содержащей M бракованных изделий.

Дискретная величина, распределенная по этому закону имеет математическое ожидание и дисперсию вида:

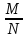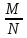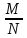M(X)= n. ; D(X)= n(1-)(1-)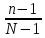

Пример 4. В ящике содержится 10 однотипных деталей. Из них 7 хорошие, а остальные-бракованные. Из ящика наугад берут 3 детали. Составить закон распределения числа хороших деталей среди 3 отобранных. Вычислить математическое ожидание и дисперсию.

N=10, M=7, n=3, X=m

X	0	1	2	3
P(X)

Находим математическое ожидание и дисперсию:

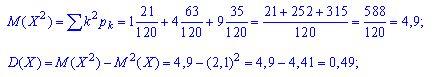
Для непрерывных величин:

Равномерное распределение

Непрерывная величина X распределена равномерно на интервале (a,b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:

f(x)=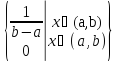

Для случайной величины X, равномерно распределенной в интервале (a,b), вероятность попадания в любой интервал (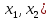, лежащий внутри интервала (a,b), равна :

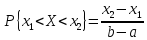
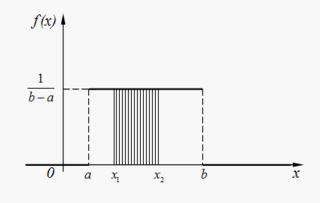
График плотности равномерного распределения:

Математическое ожидание и дисперсия для случайной величины, имеющей равномерное распределение, вычисляются по формулам:

M(X)= (a+b)/2 D(X)=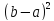/12

Пример 5: Цена деления шкалы колбы равна 0,1. Показания округляют до ближайшего деления. Найти мат. ожидание и дисперсию случайной величины- ошибки округления.

Случайная величина имеет равномерное распределение на промежутке от 0 до 0,1. M(X)=(0+0.1) /2=0.05 D(X)=0.00083

Показательное распределение

Непрерывная случайная величина X имеет показательное распределение, если плотность распределения ее вероятностей выражается формулой:

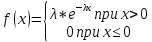
График плотности распределения вероятностей:

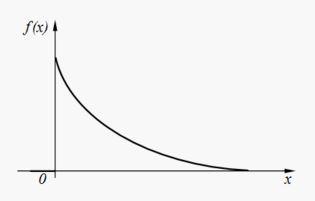
Математическое ожидание и дисперсия для случайной величины, имеющей показательное распределение, вычисляются по формулам:

M(X)=1/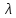

D(X)=1/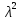

Пример 6. Случайная величина Т- время работы лампы. Найти вероятность того, что время работы лампы будет не меньше 600 часов, если в среднем лампа работает 400 часов.

Мат. ожидание равно 400, следовательно 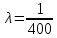. Дисперсия равна 160000.P=1-P(T<600)=1-f(600)=

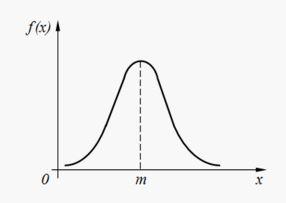
Нормальное распределение

Случайная величина X имеет нормальное распределение, если плотность распределения ее вероятностей определяется зависимостью:

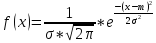
,где m=M(X).

График плотности нормального распределения: