
- •Министерство образования республики беларусь
- •Вероятность. Основные теоремы теории вероятностей
- •1. Пространство элементарных событий. Операции над случайными событиями
- •Свойства операций над событиями
- •Задачи для самостоятельного решения
- •2.Элементы комбинаторики. Непосредственный подсчет вероятностей
- •Основные комбинаторные формулы
- •Классическое определение вероятности
- •Задачи для самостоятельного решения
- •3. Геометрические вероятности
- •Задачи для самостоятельного решения
- •4. Теоремы сложения и умножения вероятностей
- •Свойства условных вероятностей
- •Задачи для самостоятельного решения
- •5. Формула полной вероятности и формула Байеса
- •Задачи для самостоятельного решения
- •6. Повторные независимые испытания (схема Бернулли)
- •Задачи для самостоятельного решения
- •Предельные теоремы для схемы Бернулли
- •Теоремы Муавра-Лапласа
- •Задачи для самостоятельного решения
3. Геометрические вероятности
Геометрическое определение вероятности может быть использовано в том случае, когда вероятность попадания случайной точки в любую часть области пропорциональна мере этой области (длине, площади, объему и т.д.) и не зависит от ее расположения и формы.
Если геометрическая
мера всей области равна S,
а геометрическая мера части этой области,
попадание в которую благоприятствует
данному событию, есть
![]() ,
то вероятность события равна
,
то вероятность события равна
![]() .
Области могут иметь любое число измерений.
.
Области могут иметь любое число измерений.
Пример 3.1.Какова вероятность того,
что сумма двух наугад взятых положительных
чисел, каждое из которых не больше
единицы, не превзойдет единицы, а их
произведение будет не больше![]() ?
?
Р ешение.
ешение.
Пусть х
и у
— взятые числа (см. рис. 3.1). Их возможные
значения
![]() ;
;![]() ,
что на плоскости соответствует квадрату
с площадью
,
что на плоскости соответствует квадрату
с площадью![]() .
Благоприятствующие значения удовлетворяют
условиям
.
Благоприятствующие значения удовлетворяют
условиям![]() и
и![]() .
Границах +
у =
= 1 делит квадрат пополам,
причем область
.
Границах +
у =
= 1 делит квадрат пополам,
причем область![]() представляет собой нижний треугольник.Вторая граница
представляет собой нижний треугольник.Вторая граница
![]() является гиперболой. Абсциссы точек
пересечения этих границ (точекВ
и С)
является гиперболой. Абсциссы точек
пересечения этих границ (точекВ
и С)
![]() и
и![]() .
Величина благоприятствующей площадиОАВСD
(на рис. 3.1 она заштрихована)
.
Величина благоприятствующей площадиОАВСD
(на рис. 3.1 она заштрихована)

Ответ:![]()
Пример 3.2. На отрезке АВ, длина которого l, наугад ставятся две точки, в результате чего этот отрезок оказывается разделенным на три части. Найти вероятность того, что из трех получившихся частей можно составить треугольник.
Р ешение.Обозначим черезх,уиl – х –
участи отрезкаАВ. Тогда
ешение.Обозначим черезх,уиl – х –
участи отрезкаАВ. Тогда![]() ;
;![]() ;
;![]() .
На плоскости этой области соответствует
треугольник, ограниченный осями координат
и прямой
.
На плоскости этой области соответствует
треугольник, ограниченный осями координат
и прямой![]() .
.
Рис. 3.2
Треугольник из полученных отрезков можно будет составить, если сумма длин двух из них превзойдет третью сторону, т.е.
![]() и
и![]() ,
,![]() .
.
Благоприятствующая площадь (см. рис. 3.2 заштрихованный треугольник) равна
![]() .
.![]() .
.
![]()
Ответ: ![]() .
.
Пример 3.3.На бесконечную шахматную
доску со стороной квадратаанаудачу
бросается монета радиуса![]() .
Найти вероятности следующих событий:А= «монета попадет целиком внутрь
одного квадрата»,В= «монета пересечет
не более одной стороны квадрата».
.
Найти вероятности следующих событий:А= «монета попадет целиком внутрь
одного квадрата»,В= «монета пересечет
не более одной стороны квадрата».
Решение.
Пусть (х,
у)
— координаты
центра упавшей монеты (рис. 3.3). В силубесконечности шахматной доски можно
считать, что элементарные исходы данного
эксперимента полностью определяются
положением центра упавшей монеты
относительно вершин квадрата, содержащего
этот центр. Помещая начало координат в
одну из вершин указанного квадрата
можно записать множество элементарных
исходов в виде![]() ,
,![]() .
Множество, соответствующее событиюА:
.
Множество, соответствующее событиюА:![]() ,
,![]() ,
т.е. является квадратом со стороной
,
т.е. является квадратом со стороной![]() .
.
Следовательно,
![]() ;
;![]() ;
;![]() .
.
Множество, соответствующее событию В, изображено на рис. 3.3.
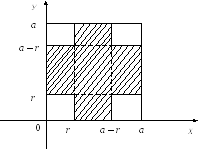
Рис. 3.3
![]() ;
;![]() ,
,![]() .
.
Ответ:![]() ;
;![]() .
.
Пример 3.4.Шар![]() помещен внутрь эллипсоида
помещен внутрь эллипсоида![]() .
Найти вероятность того, что поставленная
наудачу внутри эллипсоида точка окажется
внутри шара.
.
Найти вероятность того, что поставленная
наудачу внутри эллипсоида точка окажется
внутри шара.
Решение.
Искомая вероятность будет равна отношению
объема шара к объему эллипсоида. Объем
шара равен
![]() ,
т.е.
,
т.е.![]() .
Объем эллипсоида
.
Объем эллипсоида![]() ,
следовательно,
,
следовательно,![]() .
.![]() .
.
Ответ:![]() .
.
Пример 3.5.(Задача о встрече). Два
человека в течение промежутка времени![]() случайным образом приходят к месту
встречи и ждут время
случайным образом приходят к месту
встречи и ждут время![]() .
Какова вероятность, что они встретятся.
.
Какова вероятность, что они встретятся.
Решение.Пустьх— время прихода
первого человека, ау— второго.Хиуудовлетворяют условиям:![]() ,
,![]() .
Поскольку они приходят случайным
образом, то все исходы равновозможны иSбудет равна площади квадрата со
сторонойТ:
.
Поскольку они приходят случайным
образом, то все исходы равновозможны иSбудет равна площади квадрата со
сторонойТ:![]() СобытиеА= {они встретятся} можно
задать так
СобытиеА= {они встретятся} можно
задать так![]() .
Это множество образуют те точки, которые
лежат внутри квадрата
.
Это множество образуют те точки, которые
лежат внутри квадрата![]() ,
,![]() между прямыми
между прямыми![]() и
и![]() .
Поэтому
.
Поэтому![]() .
Искомая вероятность
.
Искомая вероятность![]() .
.
Ответ:![]() .
.
