
Програма pdfpas
Mоделювання роботи діафрагми (сепаратора)
Обєкт і мета розрахунків
1.1 Фізичний обєкт, який моделюється – плоский сепаратор в електрохімічному пристрої (електролізері або джерелі струму), який може бути або пористою діафрагмою, або нефільтруючою мембраною, товщиноюL і габаритною площею 1 см2.
Сепаратор розділяє міжелектродний простір на дві камери – анодну і катодну, в яких електроліт має різні концентрації одних і тих же компонентів. Компоненти рухаються з однієї камери в другу трьома можливими механізмами - конвекцією (фільтрація через пори із швидкістю JF см3/cсм2=см/c,в мембранах відсутня), дифузією та міграцією в електричному полі, яке утворює струм навантаження.
Рис. 1. Схема роботи сепаратора і граничні
умови задачі.
1,2 – лівий електрод і електродна камера,
3,4- правий електрод і електродна камера,
5- сепаратор, А,К- початкові (дифузійні)
профілі концентрацій аніона та катіона.
Стрілками вказані знаки напрямків
потоків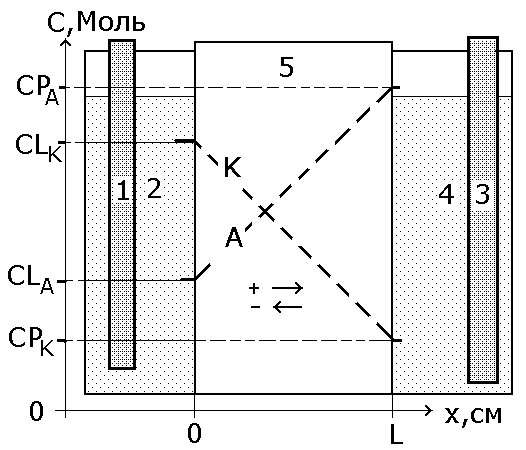
Мета роботи- вивчення закономірностей і кінетики переносу компонентів електроліту в сепараторах і розподілу їх концентрацій по товщині.
1.2 Програма розраховує стаціонарний режим переносу. Головні результати- графіки розподілу концентрацій компонентів (до 7 іонів) по глибині електрода С(x) виводяться на термінал. В файл результатів виводяться значення окремих компонентних потоків .
Математична модель і алгоритм
В сепараторі внаслідок одночасної дії на іонні компоненти електроліту закону електронейтральності і трьох механізмів переносу - міграції, дифузії та фільтрації, виникають складні нелінійні концентраційні профілі С(х), такі, що три складові частини швидкості кожного іона змінюються вдовж координати “х”, але в будь-якому перетині “х” його сумарний потік залишається незмінним. Підрахувати їх (а також потоки нейтральних речовин в молекулярній формі) за простими аналітичними формулами можна лише в окремих часткових випадках [1]. Числовим моделюванням можна знайти точне рішення.
Iтераційним методом вирішується система рівнянь переносу для всіх компонентів механізмами дифузії, фільтрації та міграції:
![]() ,
(1)
,
(1)
або в дискретній різницевій формі
![]() ,
(2)
,
(2)
де
С-концентрація
компонента, z-
його зарядове число (знак «+» або «-»),
v=DzF/RT
- рухомість іона (см/с), dU/dx=i/–градієнт
потенціалу в електроліті в порах, -
питома електропровідність розчину в
точці 0<x<L,
=L/(N-1)
-
крок дискретизації (dx),
N- кількість
точок
по координаті “х”.
Рівняння переносу те ж саме, що і для
пористого електрода, але в сепараторі
реакцій не існує, потоки компонентів
постійні (dq/dx=0),
тому права частина рівняння (1) дорівнює
нулю. Складовою частиною системи рівнянь
є рівняння електронейтральності
![]() ,
яке означає рівність сумарних концентрацій
аніонів і катіонів в будь-якій точці
координати «х»
(в перетині сепаратора площиною,
паралельною його зовнішній габаритній
поверхні).
,
яке означає рівність сумарних концентрацій
аніонів і катіонів в будь-якій точці
координати «х»
(в перетині сепаратора площиною,
паралельною його зовнішній габаритній
поверхні).
Граничні умови - задані концентрації всіх компонентів в анодній і катодній камерах. Результатом рішення є функції розподілу концентрацій по товщині сепаратора С(х) для всіх компонентів реакції.
Градієнт потенціалу електроліту dU/dx в сепараторі визначається габаритною густиною струму і та ефективною питомою електропровідністю електроліту , яка є функцією сумарної іонної концентрації компонентів, і внаслідок цього також змінюється по координаті товщини:
![]() .
(3)
.
(3)
Залежність питомої електропровідності електроліту від сумарної іонної концентрації CS в програму вводиться в формі полінома другого ступеню (параболи) з трьома коефіцієнтами а1,а2,а3:
![]() .
(4)
.
(4)
Теорія та алгоритм роботи програми наведені в [2 , с.187191], [3, c154-165].
