Розділ 2: Практичне використання методів розв’язання систем нелінійних рівнянь
2.1 Метод простих ітерацій
Програма розв’язку системи нелінійних рівнянь (СНР) методом простих ітерацій, виконана за допомогою мови програмування С++. Вхідними даними даної програми є координати точки початкових наближень. Результатом програми є точні координати точки перетину 2 функцій. Початкові наближення були визначені графічним методом.
2.1.1 Визначення початкових наближень
Результатом вирішення системи нелінійних рівнянь (2.1)є точка перетину 2 рівнянь, яка зображена на Рисунку 2.2.
(2.1)
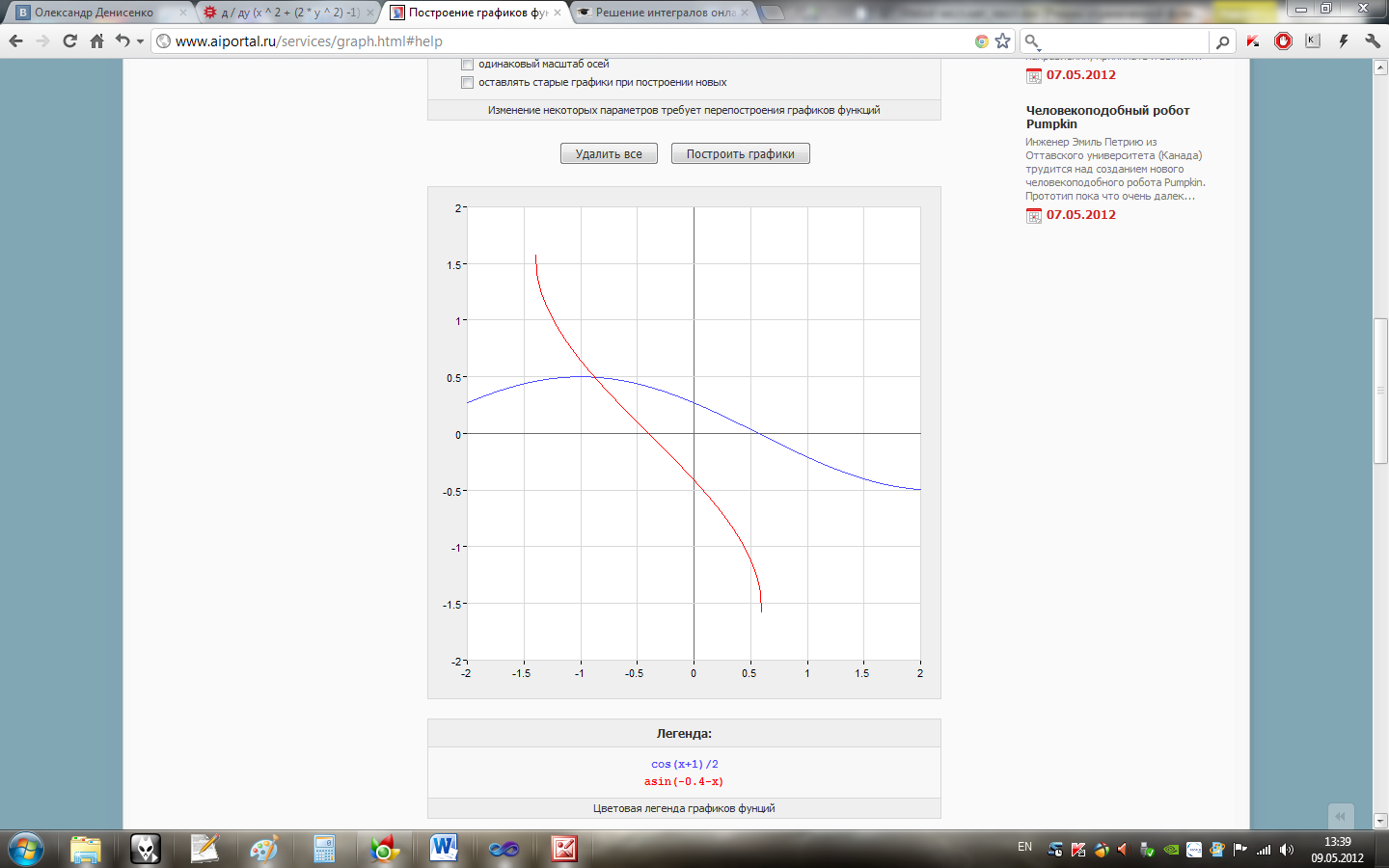
Рисунок 2.2 – Графічний метод розв’язання СНР
2.1.2 Блок-схема функції void main
Початок
e=0.001,i=0
x,y
Цикл 1
1
per[1]=f1(oldper[0])
per[0]=f2(oldper[1])
((per[0]-oldper[0])<e) и ((per[1]-oldper[1])<e)
да
нет
1
2
2
1
oldper[0]=per[0] oldper[1]=per[1]i++
Цикл 1
per[0], per[1]
Кінець
2.1.3 Код програми
#include <iostream>
#include <math.h>
#include<conio.h>
using namespace std;
float f1(float x)
{
return cos(x+1)/2;
}
float f2(float y)
{
return -0.4-sin(y);
}
void main()
{
float e=0.001,oldper[2],per[2];
int i=0;
cout<<"Metod iteracii:\n";
cout<<"Nachalniye pribligeniya:\n";
cout<<"X=";
cin>>oldper[0];
cout<<"Y=";
cin>>oldper[1];
while(1)
{
per[1]=f1(oldper[0]);
per[0]=f2(oldper[1]);
if(((per[0]-oldper[0])<e)&&((per[1]-oldper[1])<e)) break;
oldper[0]=per[0];
oldper[1]=per[1];
i++;
}
cout<<"Rezultat:\n";
cout<<"iteracii="<<i<<endl;
cout<<"X="<<per[0]<<endl;
cout<<"Y="<<per[1];
getch();
}
2.1.4 Результат роботи програми
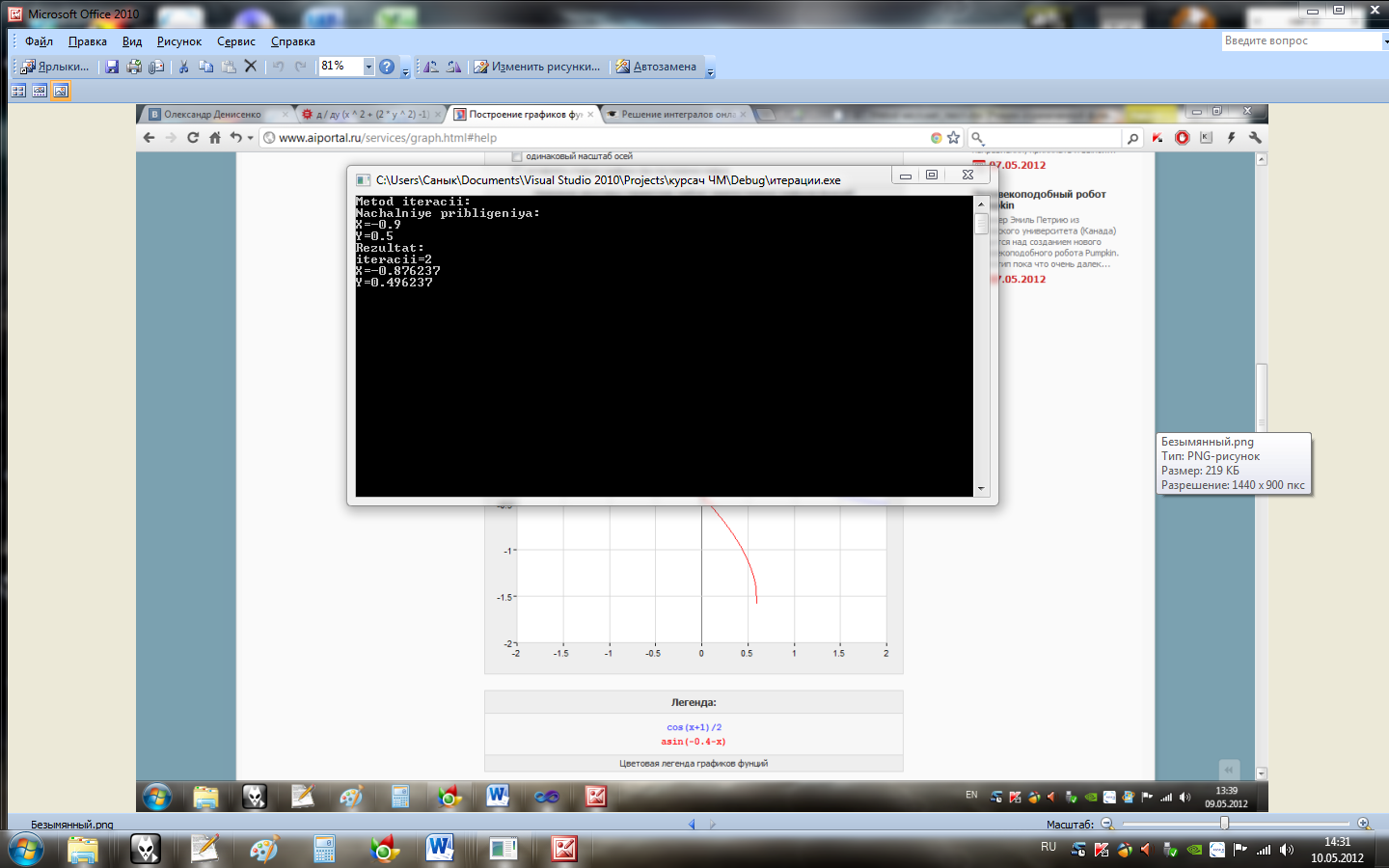
2.1.5 Обчислення які виконувались
2.2 Метод Ньютона
Програма розв’язку системи нелінійних рівнянь методом Ньютона виконана за допомогою мови програмування С++. Вхідними даними даної програми є координати точки початкових наближень. Результатом програми є точні координати точки перетину 2 функцій. Початкові наближення були визначені графічним методом.
2.2.1 Визначення початкових наближень
Результатом вирішення системи нелінійних рівнянь(2.3) е точка перетину 2 рівнянь, яка зображена на рисунку 2.4:
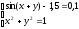(2.3)
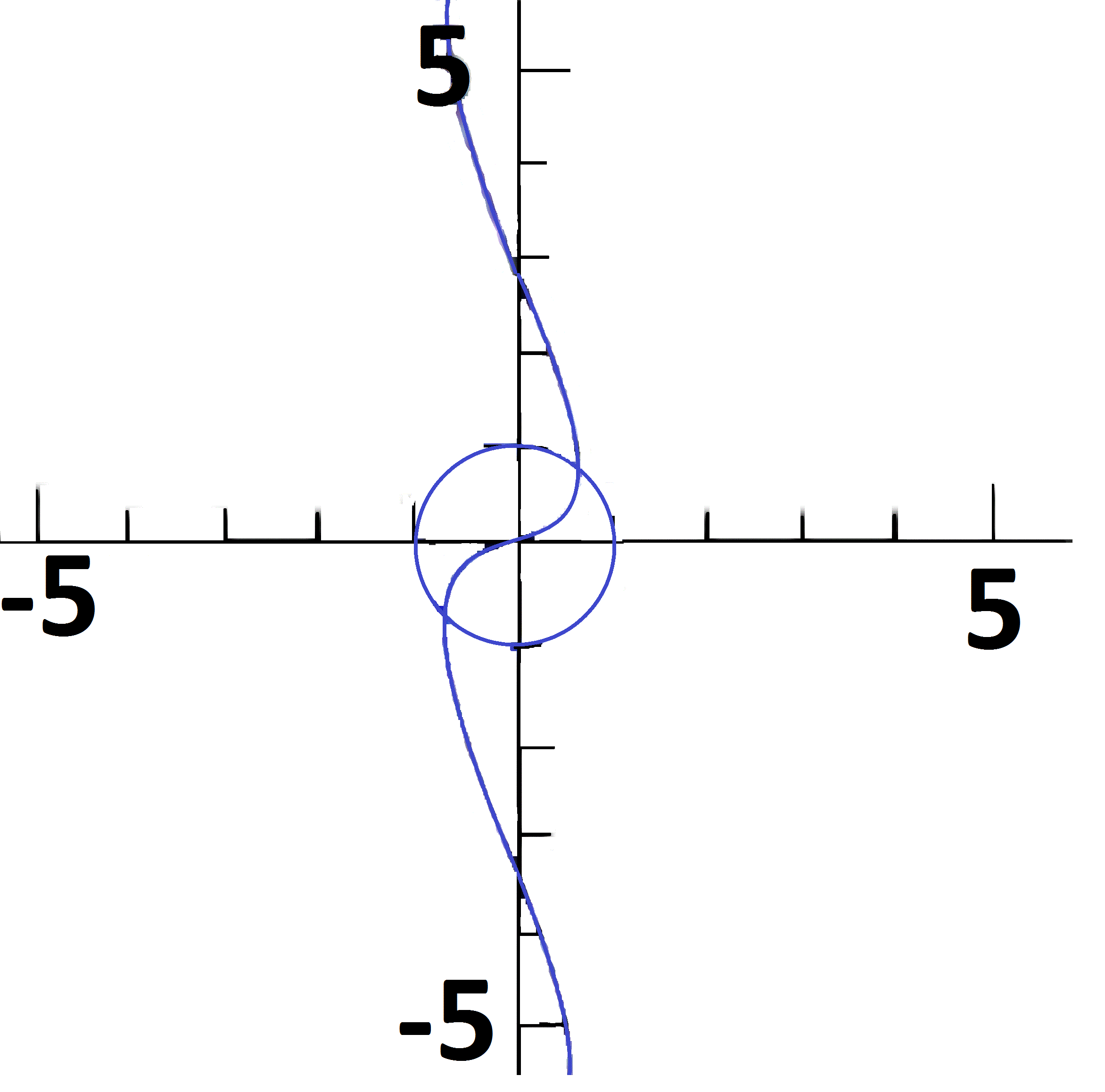
Рисунок 2.4 – Графічний метод розв’язання СНР
Як видно з Рисунку 2.4 система рівнянь має 2 розв’язки. Для знаходження цих точок методом Ньютона необхідно ввести декілька точок наближення, тобто декілька разів запустити програму на виконання.
2.2.2 Блок-схема функції void main
Початок
iter=0
fun(xk)
Цикл 1
i=0..n-1
xk[i]
Цикл 1
Кінець
2.2.3 Код програми
#include<iostream>
#include <math.h>
#include <conio.h>
using namespace std;
// Количество уравнений
const int n = 2;
void GaussSolve (double A[][n],double b[],double x[]);
double f1(double x[]);
double f2(double x[]);
double df1_dx(double x[]);
double df1_dy(double x[]);
double df2_dx(double x[]);
double df2_dy(double x[]);
double norm (double x[]);
double fun(double x[]);
int main()
{
int i, iter=0;
double xk[n];
cout<<"Reshenie SNY metodom Newton\n";
fun(xk);
cout<<"Vektor resheniia: ";
for (i=0;i<n;i++)
{
cout<<xk[i]<<" ";
}
cout<<"\n";
getch();
return 0;
}
double f1(double x[n])
{
return sin(x[0]+x[1])-(1.5*x[0])-0.1;
}
double f2(double x[n])
{
return pow(x[0],2)+pow(x[1],2)-1;
}
double df1_dx(double x[n])
{
return cos(x[0]+x[1])-1.5;
}
double df1_dy(double x[n])
{
return cos(x[0]+x[1]);
}
double df2_dx(double x[n])
{
return 2*x[0];
}
double df2_dy(double x[n])
{
return 2*x[1];
}
double norm (double x[n])
{
double sum = 0;
for (int i=0;i<n;i++)
{
sum+=x[i]*x[i];
}
return sqrt(sum);
}
double fun(double x[n])
{
int i, iter=0;
// Точность
double eps=0.001;
// Матрица
double A[n][n];
// Вектор правых частей
double b[n];
// Вектор решения
double xk[n],p[n];
// начальное приближение
cout<<"vvedite nachalniye priblogeniya:\n";
cout<<"x=";
cin>>xk[0];
cout<<"y=";
cin>>xk[1];
cout<<endl;
do
{
iter++;
for (i=0;i<n;i++)
{
x[i] = xk[i];
}
// Заполнение матрицы A
A[0][0]=df1_dx(x); A[0][1]=df1_dy(x);
A[1][0]=df2_dx(x); A[1][1]=df2_dy(x);
// Заполнение вектора правых частей
b[0]=-f1(x); b[1]=-f2(x);
GaussSolve (A,b,p);
// Получаем следующее приближение,
// складывая предыдущее и вновь полученное
for (i=0;i<n;i++)
{
xk[i] = x[i] + p[i];
}
}
while (fabs(norm (x) - norm(xk))>=eps);
cout<<"Reshenie nadeno za "<<iter<<" iterazii\n";
return xk[i];
}
void GaussSolve (double A[n][n],double b[n],double x[n])
// Решение СЛУ методом Гаусса
{
const double eps=0.001;
double tmpValue;
int i,j,k,z;
double dblLeadElement;
// Прямой ход
for(i=0; i<n; i++)
{
dblLeadElement=A[i][i];
// Находим строку, в которой элемент, стоящий под ведущим - наибольший
double tmpMax = dblLeadElement;
int tmpMaxNumber = i;
for (z=i;z<n;z++)
{
if (A[z][i]>tmpMax){tmpMax = A[z][i];tmpMaxNumber=z;}
}
// Меняем местами i-ю строку и строку tmpMaxNumber
for (z=i;z<n;z++)
{
tmpValue = A[i][z];
A[i][z] = A[tmpMaxNumber][z];
A[tmpMaxNumber][z] = tmpValue;
}
tmpValue = b[i];
b[i] = b[tmpMaxNumber];
b[tmpMaxNumber] = tmpValue;
dblLeadElement = tmpMax;
for(j=i; j<n; j++)
{
A[i][j]/=dblLeadElement;
}
b[i]/=dblLeadElement;
for(k=i+1; k<n; k++)
{
double dblToDivide=A[k][i]/A[i][i];
for(z=i;z<n; z++)
{
A[k][z]-=A[i][z]*dblToDivide;
}
b[k]-=b[i]*dblToDivide;
}
}
// Обратный ход
x[n-1]=b[n-1];
for(k=n-2; k>=0; k--)
{
double sum=b[k];
for(j=k+1; j<n; j++)
{
sum-=A[k][j]*x[j];
}
x[k]=sum;
}
}