Розв’язуючи ці рівняння щодо коефіцієнтів і, знаходимо: ; (14.28) . (14.29)

Підставляючи вирази для коефіцієнтів (14.28), (14.29) у формули (14.23)(14.25), одержимо формули Ламе для визначення радіального переміщення і напружень:

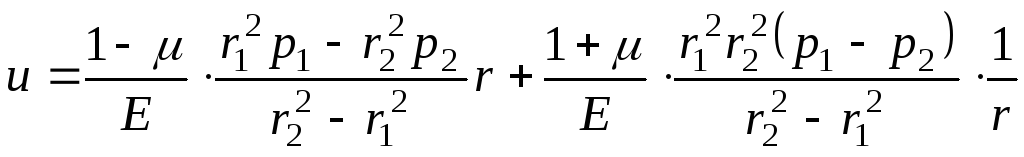; (14.30)

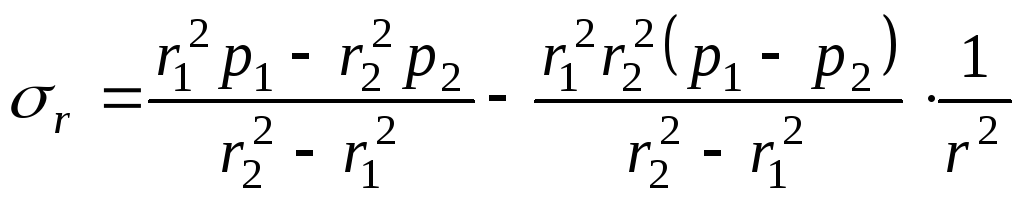; (14.31)

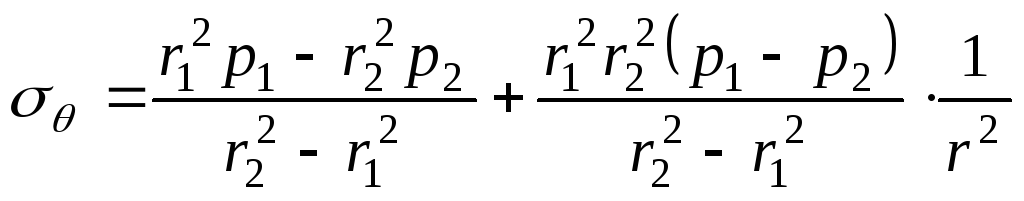. (14.32)

Якщо скласти ліві і праві частини виразів для і, можна переконатися в тому, що сума радіального та колового напружень є величиною сталою:

.

Відносна деформація вирізаного з тіла циліндра кільця одиничної ширини в напрямку осі циліндра, також буде сталою:

.

Отже, циліндр можна розглядати, як складений з окремих кілець, нанизаних на вісь. Поперечні перерізи циліндра при деформації залишаються плоскими.

Формули Ламе виводилися для циліндра, у якого відсутнє днище. При наявності днища в поперечних перерізах виникають осьові напруження (Рис.14.16).

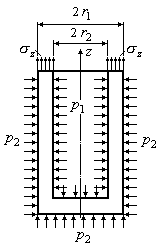
Рис.14.16

Допускаючи рівномірний розподіл напружень по товщині стінки, що є цілком справедливим вдалині від днища, і складаючи рівняння рівноваги на вісь, одержимо:

.

Звідки

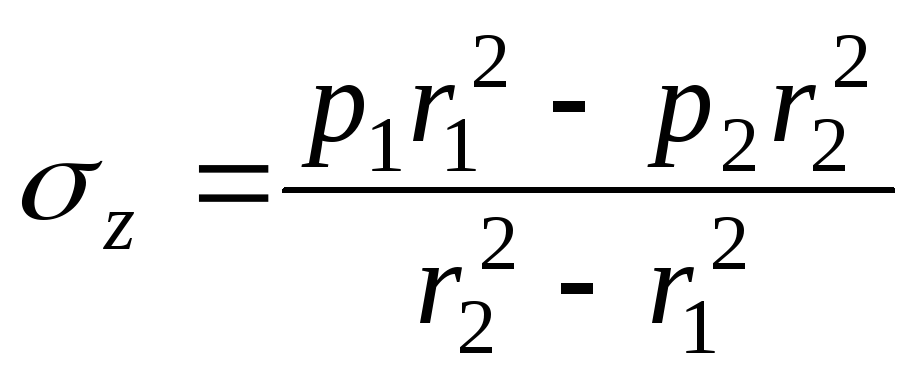. (14.33)

Порівнюючи цю формулу з рівняннями (14.31), (14.32), легко встановлюємо, що в даному випадку осьове головне напруження є середнім арифметичним між коловим і радіальним напруженнями:

.

Знаючи осьове напруження , визначимо збільшення радіального переміщення:

.

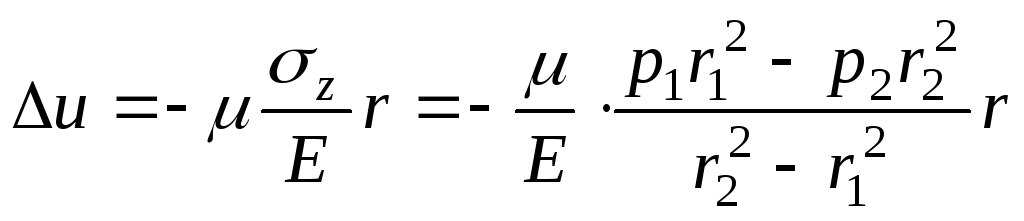При наявності днища це збільшення варто додати до радіального переміщення, розрахованого за формулою (14.30).

Розглянемо кілька окремих випадків навантаження циліндра [3].

14.5. Окремі випадки розрахунку товстостінних циліндрів

1. Циліндр навантажений тільки внутрішнім тиском, зовнішній тиск малий або їм можна знехтувати, тобто ;.Формули для напружень і радіальних переміщень виглядають так:

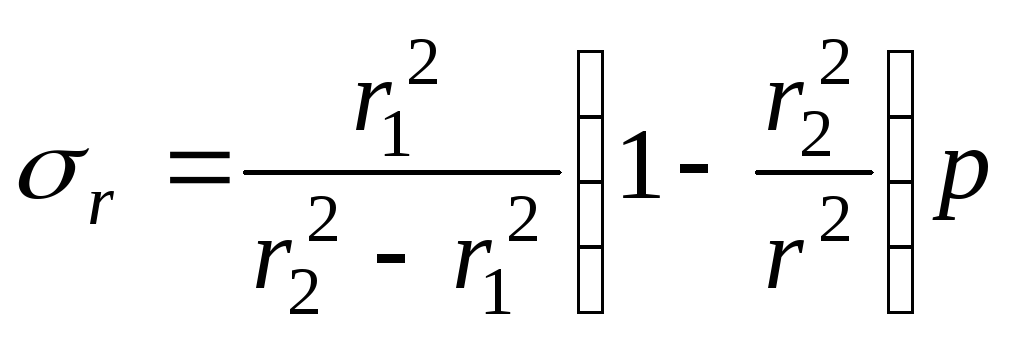; (14.34)

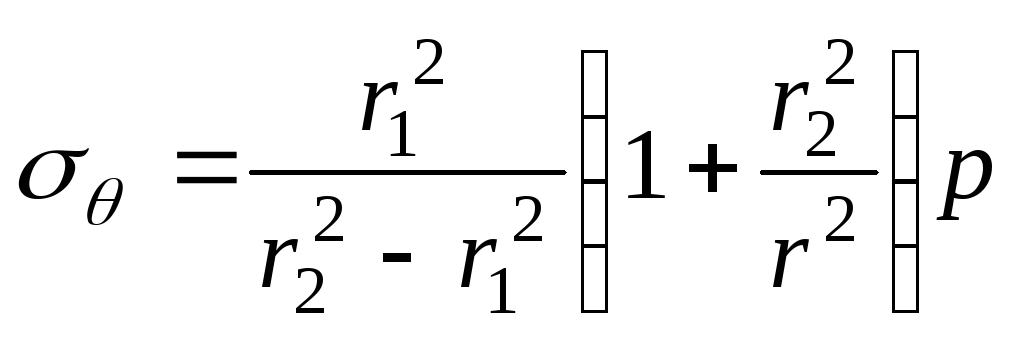; (14.35)

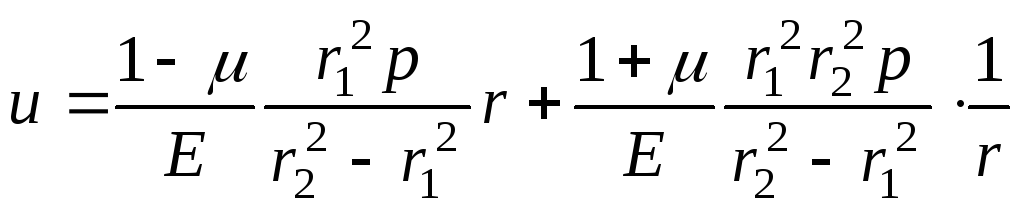; (14.36)

Зазвичай один з радіусів циліндра – внутрішніх або зовнішній – буває відомий з умов, що випливають з призначення конструкції, наприклад, внутрішній діаметр циліндра відомий з умови його вантажної під’ємності і тискові рідини. Тому вирази (14.34)(14.36) зручно привести до такого виду, при якому шуканим є відношення радіусів . Виразимо за допомогою цього відношення радіальні й колові напруження на внутрішній поверхні циліндра (при):

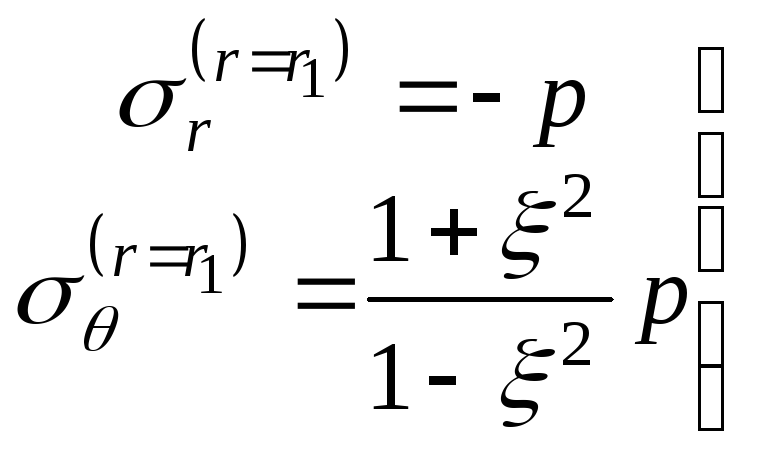. (14.37)

Радіальні переміщення внутрішньої поверхні (збільшення внутрішнього радіуса циліндра) дорівнюватиме:

. (14.38)

Напруження і переміщення на зовнішній поверхні циліндра будуть такими:

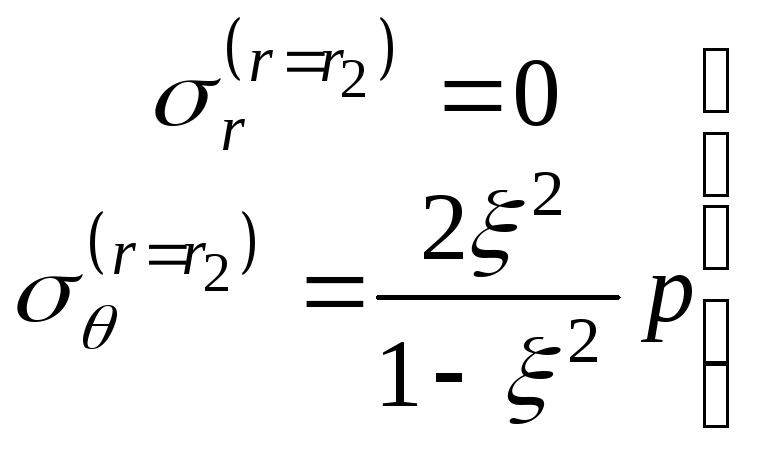; (14.39)

. (14.40)

Епюри напружень ідля розглянутого випадку при відношеннінаведені на рис. 14.17,а.

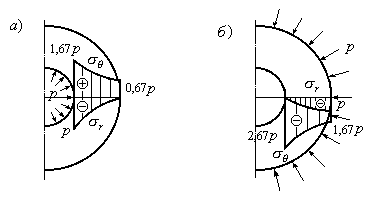
Рис.14.17

Найбільш небезпечною з точки зору міцності є точка, що знаходиться у внутрішньої поверхні циліндра.

Визначимо допустимий внутрішній тиск у циліндрі при безмежному збільшенні товщини стінки. Припускаючи і приймаючи в формулах (14.37), одержимо;.

Використаємо третю теорію міцності і з огляду на те, що у випадку, що розглядається, ;, одержуємо:

,

звідки

.

Таким чином, циліндр навіть з товщиною стінки нескінченно великою не витримує за міцністю, якщо внутрішній тиск перевищує половину величини допустимого напруження, прийнятого для матеріалу циліндра. У даному випадку збільшення товщини стінки не гарантує збільшення міцності.

2. Циліндр навантажений тільки зовнішнім тиском: ;. У цьому випадку формули Ламе для напружень (14.31), (14.32) і для переміщень (14.33) набувають наступного вигляду:

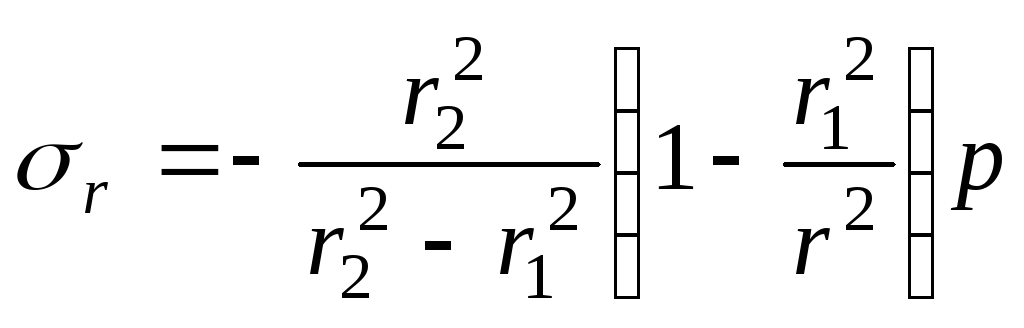; (14.41)

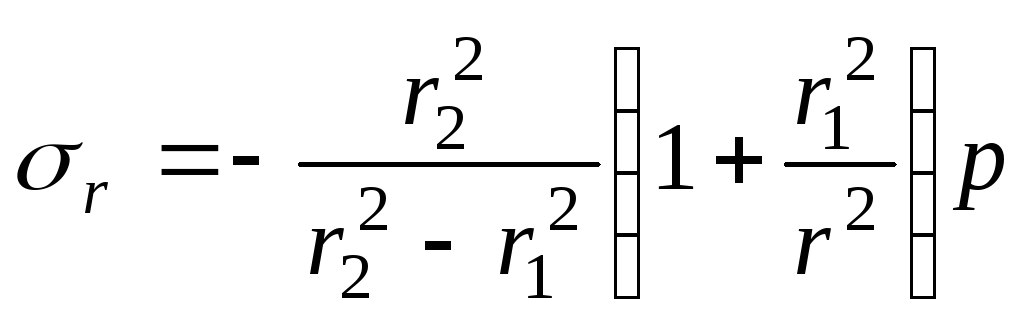; (14.42)

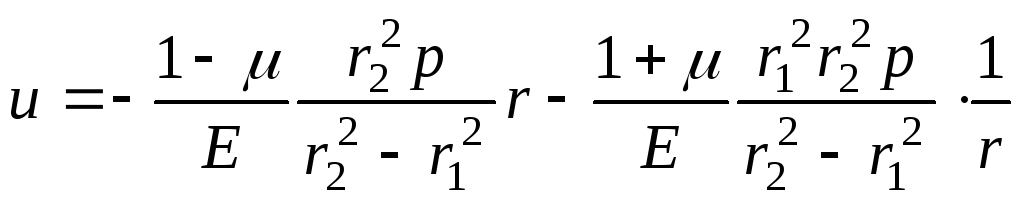; (14.43)

Обоє напруження стискальні, причому за абсолютною величиною , а радіальне переміщення спрямовано до осі стержня (радіуси зменшуються).

У внутрішньої поверхні циліндра напруження дорівнюватимуть:

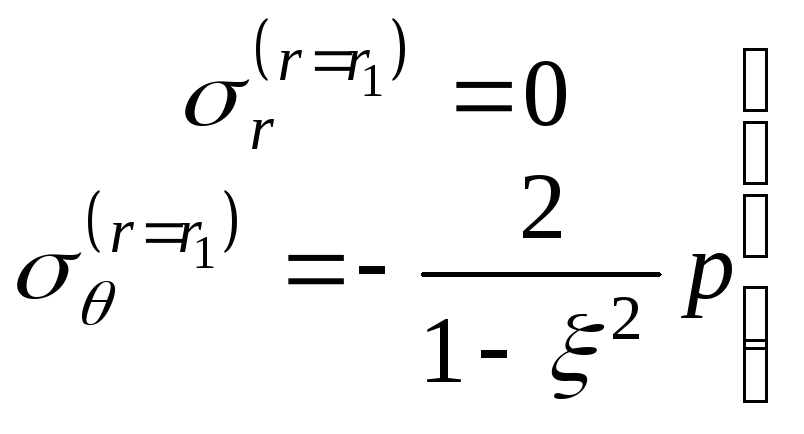. (14.44)

Радіальне переміщення внутрішньої поверхні стінки циліндра дорівнюють:

. (14.45)

У зовнішньої поверхні циліндра:

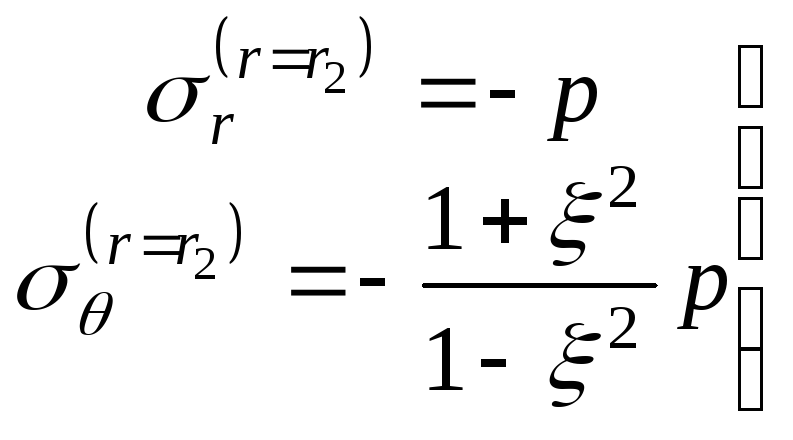; (14.46)

. (14.47)

Епюри напружень ідля випадку, що розглядається, при відношеннінаведені на рис.14.17,б. Найбільшого значення за абсолютною величиною напруженнядосягає у внутрішньої поверхні циліндра. У точках внутрішньої поверхні виникає лінійний напружений стан, напруженняпри,,. Так само, як і в попередньому окремому випадку навантаження максимальна величина допустимого зовнішнього тиску не може перевищувати половини величини допустимого напруження, встановленого для матеріалу циліндра.