3.9. Потенциальная энергия деформации при осевом растяжении и сжатии

Потенциальной энергиейназывается энергия, накапливаемая в образце при его упругих деформациях. Потенциальная энергия численно равняется работе внешних сил, приложенных к телу, на вызванных ими перемещениях. За счет потенциальной энергии восстанавливаются первоначальная форма и размеры образца при снятии нагрузки.

Рассмотрим стержень, растянутый силой на величину. Растягивающая сила в процессе деформации медленно росла от 0 дои совершала работу, которая в переделах упругих деформаций численно равняется потенциальной энергии деформации:

.

Пусть в процессе деформации сила приняла некоторое значение. При этом удлинение стержня стало равным(Рис.3.15,а). Дадим силеприращение, тогда удлинение вырастет на величину. Элементарная работа силына этом преремещении будет равна:

.

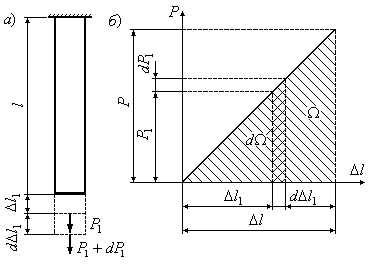
Рис.3.15

Пренебрегая величиной второго порядка малости выражение для элементарной работы получаем в виде:

.

На рис.3.15,б приведена диаграмма растяжения стержня в зоне упругих деформаций. Из рисунка видно, что величина равна площади узкой заштрихованной полоски диаграммы:

. (3.17)

Всю работу на упругой деформации вычислим, проинтегрировав выражение (3.17) по всей площади диаграммы:

.

Таким образом, работа и, следовательно, потенциальная энергия равны площади диаграммы растяжения, которая в пределах упругих деформаций имеет вид треугольника:

. (3.18)

Подставляя в формулу (3.18) вместо силы равное ей внутреннее усилиеи удлинение (3.7), получим:

. (3.19)

Анализируя выражение (3.19), приходим к выводу, что потенциальная энергия всегда будет положительной. Вследствие нелинейности функции (3.19) при вычислении потенциальной энергии нельзя пользоваться принципом независимости действия сил. Непосредственно выражением (3.19) можно пользоваться для вычисления потенциальной энергии лишь в том случае, если продольная сила на участке будет иметь постоянное значение. Если же площади поперечного сечения и продольные силы на участках стержня будут разными, то при скачкообразном изменении этих величин потенциальную энергию вычисляют на каждом участке отдельно, а результаты подсчетов складывают:

. (3.20)

Если же площадь поперечного сечения или продольное усилие меняются по длине постепенно в соответствии с каким-либо законом, то сначала записывают выражение для потенциальной энергии бесконечно малого отрезка стержня длиной , на протяжении которого и площадь поперечного сечения и продольное усилие могут считаться постоянными:

,

а затем интегрируют это выражение по длине стержня. Тогда вся потенциальная энергия, накапливаемая в стержне, будет равна:

. (3.21)

Энергия, затраченная на деформацию единицы объема материала в пределах упругости, называется удельной потенциальной энергиейи обозначается буквой. Для стержня, растягиваемого силой(Рис.3.15,а), удельная потенциальная энергия равна:

, (3.22)

где объем образца перед началом нагружения.