9.4.2. Напряжения на произвольно наклоненных площадках

Получим формулы для напряжений и, действующих на произвольно ориентированной площадке, Положение этой площадки определим углами, образованными нормальюк этой площадке с осями 1, 2 и 3, соответственно параллельными главным напряжениями. Формулы для напряженийиполучим из условия равновесия элементарного четырехгранника (тетраэдра), приведенного на рис.9.21, выделенного из главного параллелепипеда.

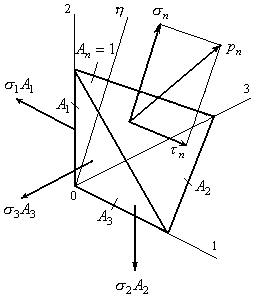
Рис.9.21

Примем площадь , тогда площади других граней тетраэдра как проекциина координатные плоскости примут вид:

;;. (9.44)

Проектируя все силы на нормаль , найдем

, (9.45)

откуда, учитывая (9.44), получим формулу для нормального напряжения:

. (9.46)

Так как нам неизвестно направление касательного напряжения , то найдем прежде полное напряжение.

Если в пространстве построить многоугольник сил, действующих на тетраэдр, то вектор будет диагональю параллелепипеда, у которого ребра равны. Таким образом:

.

Отсуда, используя (9.44), получим полное напряжение:

. (9.47)

Теперь можно определить касательное напряжение:

. (9.48)

Формулы (9.46)-(9.48) показывают, что три главных напряжения ивполне определяют объемное напряженное состояние.

9.4.3. Октаэдрических напряжения. Понятие об интенсивности напряжений

Площадка, равнонаклоненная к направлению трех главных напряжений, называется октаэдрической, а действующие на ней напряжения –октаэдрическими напряжениями. Указанные площадки отсекают на осях 1,2 и 3 равные отрезки и образуют в простроанстве восьмигранник – октаэдр (Рис.9.22).

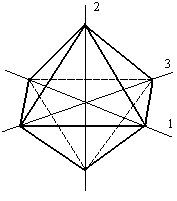
Рис.9.22

Косинусы углов являются направляющими косинусами для нормалии поэтому связаны соотношением:

.

Для октаэдрических площадок и, следовательно,

.

Подставляя это значение косинусов в (9.46) и (9.47), найдем:

. (9.49)

. (9.50)

По формуле (9.48)

.

Отсюда окончательно имеем:

. (9.51)

При изучении вопросов прочности тел общая деформация материала в окрестности точки подразделяется на деформации измененеия объема и формы. Важное значение октаэдрических напряжений определяется тем, что с первой из этих деформаций связано напряжение , а со второй.

Зная касательные октаэдрические напряжения, можно рассчитать интенсивностьнапряжений:

(9.52)

или

(9.53)

9.5. Деформированное состояние в точке