9.5.2. Закон Гука при плоском и объемном напряженном состоянии

Рассмотрим элемент, выделенный из центрально растянутого стержня (Рис.9.24).

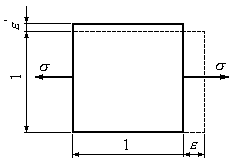
Рис.9.24

Элемент испытывает продольную и поперечную деформации, связанные с напряжениями формулами:

; (9.71)

. (9.72)

Здесь: модуль упругости при растяжении (сжатии), акоэффициент Пуассона. Деформация удлинения считается положительной, укорочения – отрицательной.

Формула (9.71) выражает закон Гука при простом растяжении (линейное напряженное состояние). Установим аналогичное соотношение при объемном напряженном состоянии.

Найдем главные деформации , выразив их через главные напряжения. Для этого воспользуемся принципом независимости действия сил и соотношениями (9.71) и (9.72). Суммарное относительное удлинениепо направлению напряженияможно представить тремя слагаемыми:

,

где деформация, возникающая при действии только напряженияи определяемая по формуле (9.71), так как эта деформация является продольной по отношению к(Рис.9.25а).

 удлинение, вызванное напряжением. Это поперечнае по отношению кдеформация (Рис.9.25б), которая определяется по формуле (9.72).

 деформация, вызванная напряжением.

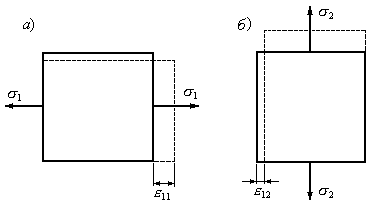
Рис.9.25

Следовательно:

.

Применяя подобные рассуждения к определению и, получим формулы закона Гука при объемном напряженном состоянии (обобщенный закон Гука):

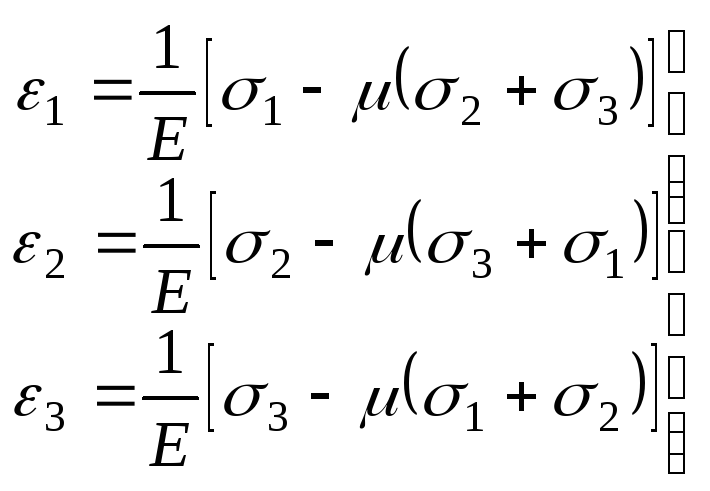. (9.73)

В эти формулы растягивающее напряжение подставляется со знаком “плюс”, а сжимающие – со знаком“минус”.

При равенстве нулю одного из трех главных напряжений имеем плоское напряженное состояние. В этом случае, например, при , получим:

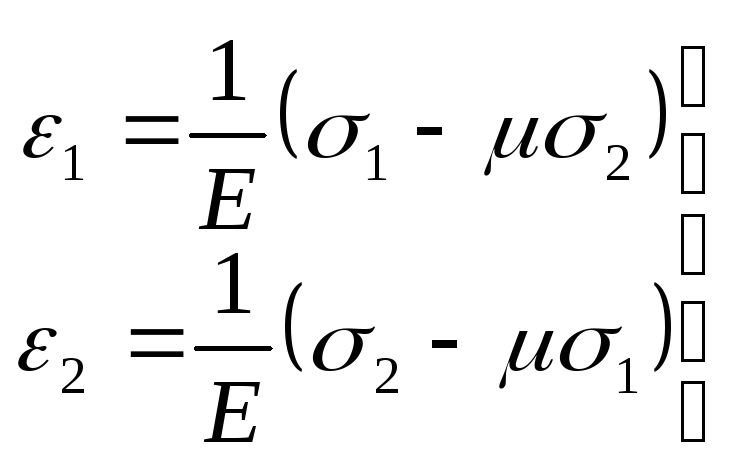.(9.74)

Следует отметить, что равенство нулю напряжения не означает, что также равно нулю. Действительно, приимеем:

. (9.75)

При известных напряжениях ипо формулам (9.74) определяют дефомациии. Но в некоторых случаях необходимо иметь обратную зависимость. Умножая вторую строку формулы (9.74) наи складывая с первой, получим:

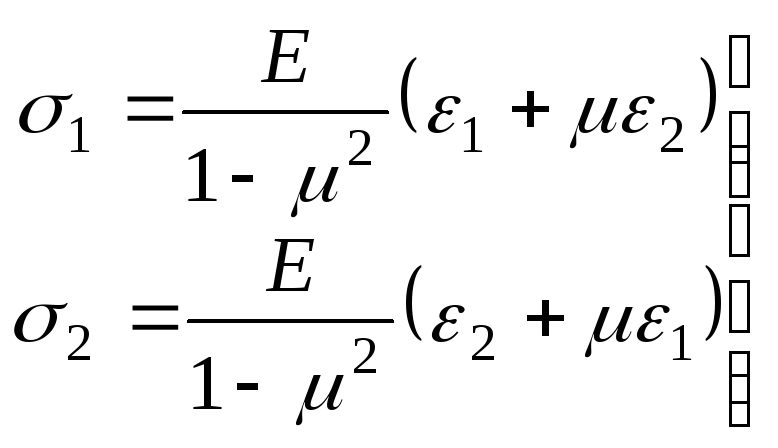.(9.76)

Полученные формулы написаны применительно к главным площадкам и напряжениям. Однако, следует иметь ввиду, что и для неглавных площадок закон Гука, связывающий нормальные напряженияии соответствующие удлиненияи, имеет тот же вид:

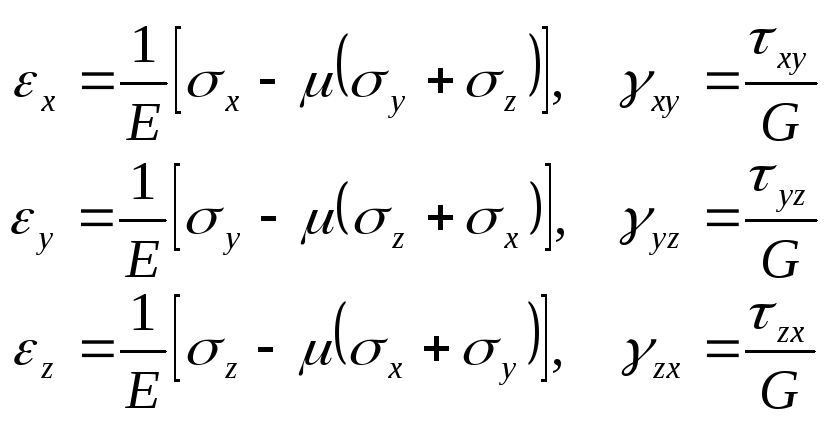, (9.77)

где модуль сдвига.

Причина состоит в том, что при малых деформациях влияние сдвига на линейную деформацию представляет собой величину второго порядка малости, которой можно пренебречь.

9.5.3.Объемная деформация. Объемный закон Гука

Обозначим размеры сторон элементарного параллелепипеда до деформации через (Рис.9.26а). После деформации эти размеры увеличатся и станут равными,,(Рис.9.26б). Начальный объем параллелепипеда обозначим, а после деформации.

Найдем абсолютное изменение объема параллелепипеда:

. (9.78)

Здесь в скобках стоят относительные удлинения:

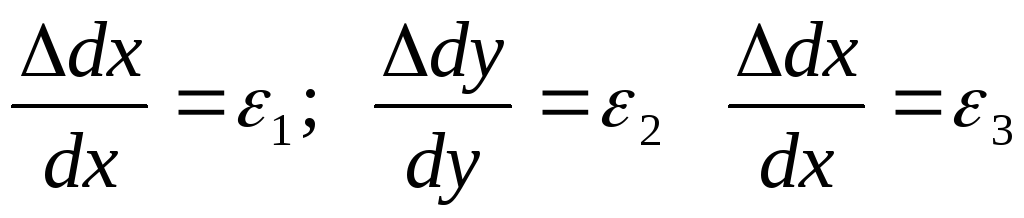. (9.79)

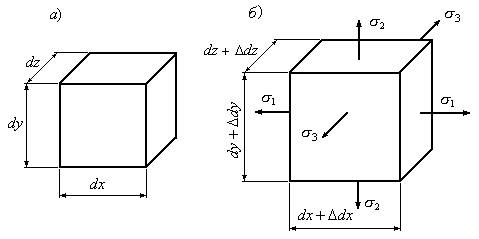
Рис.9.26

Подставляя в (9.79) в (9.78) и перемножая выражения в скобках, получаем:

.

Пренебрегая произведениями относительных удлинений ввиду их малости, имеем:

(9.80)

Относительное изменение объема или относительная объемная деформация принимает вид:

. (9.81)

Эта формула справедлива как для упругих, так и для упруго-пластических деформаций.

Для упругой стадии работы материала можно выразить относительное изменение объема через напряжения . Для этого подставим значенияиз выражения (9.73) в выражение (9.81):

.

После преобразования, получим:

. (9.82)

В частности, при равномерном всестороннем сжатии, когда

. (9.83)

Из выражения (9.83) следует, что коэффициент Пуассона не может быть больше 0,5, так как в противном случае при всестороннем сжатии тело будет не уменьшаться, а увеличиваться в объеме, что противоречит физическому смыслу. Этот вывод подтверждается опытными данными. В природе не обнаружено материалов, у которых коэффициент Пуассона был бы больше 0,5.

Существуют материалы (например, парафин), у которых коэффициент Пуассона приближается к величине 0,5. В этом случае, при всестороннем сжатии не будет происходить изменения объема. Таким образом, парафин по своим упругим свойствам приближается к несжимаемой жидкости.

Для пластической стали, находящейся в состоянии текучести, коэффициент Пуассона также близок к 0,5. В связи с этим объем образца из пластической стали во время текучести не меняется.

Вычислим теперь среднее напряжение (Рис.9.26,б):

.

Подставляя среднее напряжение в формулу (9.82), получим:

, (9.84)

где

. (9.85)

Величина называется модулем объемной деформации, а выражение (9.84) –объемным законом Гука. В соответствии с этим закономотносительное изменение объема пропорционально среднему напряжению.