9.4. Объемное напряженное состояние

9.4.1. Понятие о тензоре напряжений. Экстремальные касательные напряжения

Случай объемного напряженного состояния представлен на рис.9.2. Как уже отмечалось у разделе 9.1 настоящего пособия, на каждой из граней действует нормальное напряжение , а также по две составляющие касательного напряжения.

Таким образом, напряженное состояние в выделенном элементарном параллелепипеде в общем случае характеризуется девятью компонентами напряжений, которые могут быть записаны в виде тензора напряжений:

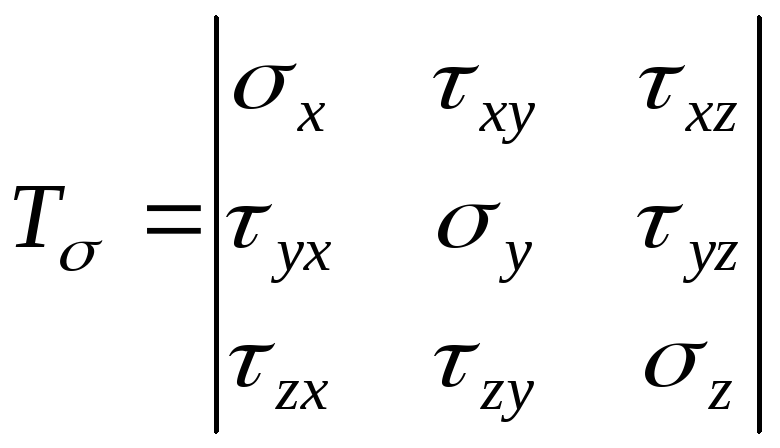. (9.25)

Касательные напряжения, представленные тензором напряжения, связаны рядом зависимостей, получить которые можно, составив уравнение суммы моментов всех сил относительно координатных осей (Рис.9.2):

;;. (9.26)

Модули этих напряжений одинаковы, а знаки на основании закона парности касательных напряжений (9.8) противоположны.

Общий случай напряженного состояния (Рис.9.19а) может быть представлен в виде суммы двух напряженных состояний, характеризуемых в первом случае одинаковыми нормальными напряжениями (Рис.9.19,б) и во втором случае (Рис.9.19,в) – нормальными напряжениями:

;;(9.27)

и касательными напряжениями .

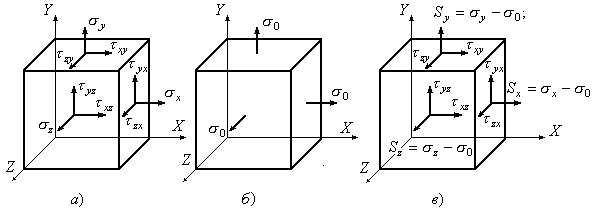
Рис.9.19

Примем:

. (9.28)

Тогда из (9.27) следует:

. (9.29)

Напряженное состояние, представленное на рис.9.19,б, может быть описано шаровым тензором напряжений:

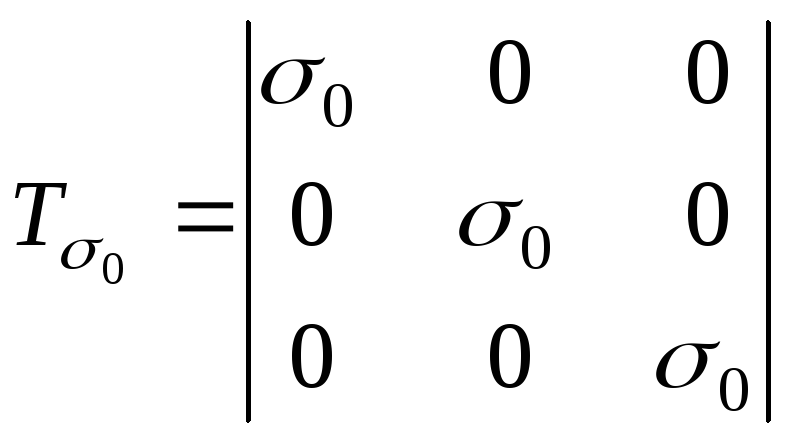. (9.30)

Напряженное состояние, представленное на рис.9.19,в, может быть описано тензором, который назывется девиатором напряжений:

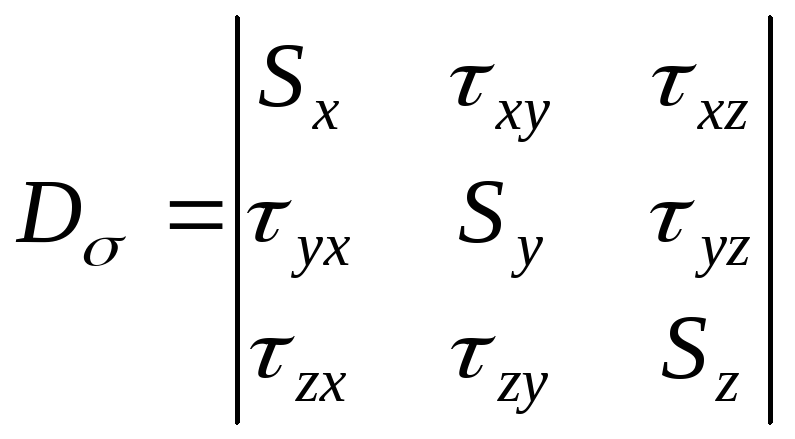. (9.31)

Шаровой тензор характеризует изменение объемавыделенного элемента, девиатор характеризует изменениеформыэлемента.

Рассмотрим определение главных напряжений и, через напряжения, действующие на произвольных площадках (Рис.9.19,а). Предположим, что нам известно положение главной площадки, определяемое наклоном нормали к этой площадкепо отношению к осям координат. Сечением, параллельным этой площадке, выделим из исходного параллелепипеда тетраэдр, изображенный на рис.9.20, и составим условия равновесия тетраэдра в виде сумм проекций всех действующих сил на оси координат.

Рис.9.20

Косинусы углов, образованные нормалью с осями координат, обозначим соответственно. Примем площадь наклонной грани, тогда площади других граней, лежащих в координатных плоскостях, будут,,. На главной площадке касательные напряжения отсутствуют. Действующее здесь главное напряжениеобозначим. Сумма проекций сил на осьдает:

.

Проектируя все силы на оси и, получим еще два аналогичные уравнения. Таким образом, будем иметь следующие три уравнения равновесия тетраэдра:

. (9.32)

Уравнения (9.32) можно рассматривать как однородную систему уравнений относительно неизвестных . Между направляющими косинусами нормалисуществует зависимость

, (9.33)

поэтому они не могут одовременно равняться нулю. Известно, что при этом условии определитель системы (9.32) должен быть равен нулю, т.е.

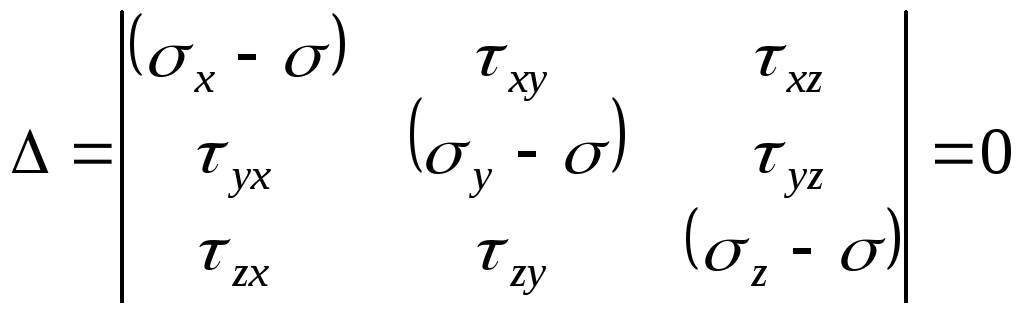. (9.34)

Раскрыв определитель (9.43), придем к кубическому уравнению:

, (9.35)

три корня которого представляют сосбой главные напряжения .

Коэффициенты уравнения (9.35) принимают вид:

; (9.36)

;(9.37)

.(9.38)

Поскольку главные напряжения не зависят от выбора осей координат, коэффициенты кубического уранения (9.35) также не изменяются при повороте осей координат, т.е. являются инвариантамии называются соответственно, первым, вторыми третьиминвариантами тензора напряжений. Из формул (9.36)-(9.38) следует, что выражения инвариантов тензора напряжений через главные напряжения имеют вид:

; (9.39)

;(9.40)

.(9.41)

В частном случае плоского напряженного состояния кубическое уравнение (9.35) сводится к квадратному, два корня которого дают значения и, совпадающими с формулами (9.19), полученными выше. В этом случае нужно положить, так как граньисходного параллелепипеда должна быть свободна от напряжений.

Для определения направляющих косинусов и, соответствующих одному из трех главных напряженийи, нужно значение этого главного напряжения подставить в выражение (9.32) вместо. Совместное решение уравнений (9.32) даст искомые величиныи.

Для определения максимальных касательных напряжений примем, что главные напряжения иизвестны. Как и при плоском напряженном состоянии максимальные каксательные напряжения действуют в площадках, наклоненных под углом 45⁰к главным напряжениям. Касательные напряжения на этих площадках будут иметь вид:

;;. (9.42)

Наибольшее из этих напряжений определяет максимальные касательные напряжения в точке:

. (9.43)

Таким образом, в общем случае максимальное касательное напряжение в точке действует на площадке, наклоненной под углом 45⁰ к максимальному и минимальному из трех главных напряжений, и равно их полуразности.

Прочность материала или переход его под нагрузкой в пластическое состояние в ряде случаев связывают с величиной максимального касательного напряжения , и поэтому оно наряду с главными напряжениями является важной характеристикой напряженного состояния.