9.3.3. Экстремальные касательные напряжения

Примем в качестве исходных площадки, в которых действуют главные напряжения (Рис.9.13).

Рис.9.13

Отсчитывая угол от направления, напишем выражения дляи, используя формулы (9.12), (9.14), полагая в них,, а:

; (9.21)

. (9.22)

Из формулы (9.22) следует, что при синус двойного угла, касательные напряжения имеют экстремальные значения:

. (9.23)

Экстремальные касательные напряжения в точке равны полуразности главных напряжений и действуют на площадках, наклоненных к главным площадкам под углом 45⁰(Рис.9.13,а).

Подставляя (9.19) в (9.23), получим выражение через исходные напряженияи:

. (9.24)

В частном случае, когда на границах призмы действуют два главных напряжения (Рис.9.13б), экстремальные касательные напряжения (9.23) численно равны главным напряжениям:

,

а нормальные напряжения на площадках с экстремальными касательными напряжениями в этом случае равны нулю. Такой случай напряженного состояния носит название чистого сдвига, а площадки, на которых действуют одни касательные напряжения называютсяплощадками чистого сдвига.

9.3.4. Примеры исследования плоского напряженного состояния в точке

Пример 9.2.Нормальные напряжения на площадкахМПа,МПа, касательные напряженияМПа. Определить нормальные,и касательные,напряжения в площадках, нормаль к которым наклонена по отношению к осипод углами соответственнои, если=,=(Рис.9.14).

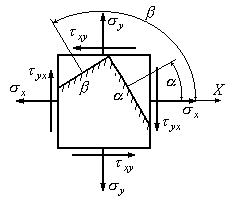
Рис.9.14

Решение:

Для определения нормального напряжения в площадке воспользуемся выражением (9.14):

МПа

Нормальное напряжение вна площадке найдем с помощью выражения (9.15):

МПа.

Для проверки используем условие инвариантности (9.16):

;.

Касательные напряжения определим из выражения (9.12):

МПа.

Касательные напряжения, действующие на площадке :

МПа.

В соответствии с законом парности касательных напряжений (9.8):

.

Следовательно, задача решена верно. Направление нормальных и касательных напряжений, действующих на площадках ипокажем на рис 9.15.

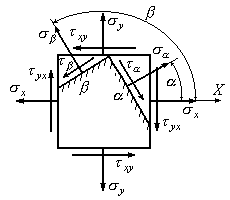
Рис.9.15

Пример 9.3. Определить величины главных напряжений ии направления главных напряжений (Рис.9.16,а). Изобразить главные площадки и главные напряжения на рисунке.

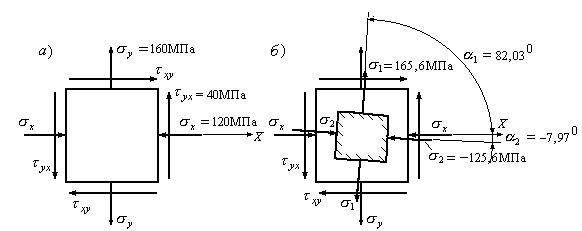
Рис.9.16

Решение:

1. Определяем максимальные нормальные напряжения из выражения (9.19):

=

МПа.

МПа.

Для проверки используем условие инвариантности (9.16):

;.

Направление главных напряжений найдем, используя выражения (9.20):

;;

;.

Для проверки правильности решения сложим абсолютные величины углов и. Так как главные оси взаимно перпендикулярны, в сумме должен получиться угол 90⁰:

.

Решение выполнено верно. Отложим найденные углы на рисунке (Рис.9.16,б) и проставим значения главных напряжений.

Пример 9.4.Определить нормальные, касательные и главные напряжения в точке А, изображенного на рисунке поперечного сечения изгибаемой балки, если изгибающий момент в сечении равенкНм, поперечная сила –кН. Найти положение главных площадок, изобразить их на рисунке, показать направления главных напряжений.

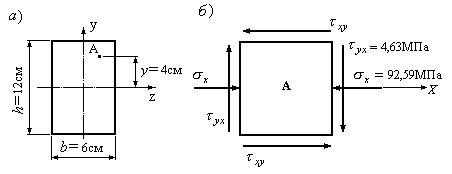
Рис.9.17.

Решение:

1. Вычисляем момент инерции поперечного сечения относительно нейтральной линии сечения , приведенного на рис 9.17а и определяем величину нормальных напряжений и касательных напряжений в точке А сечения:

см³;МПа;

МПа.

2. Вырезаем вокруг точки А элементарную площадку и прикладывем к ее граням нормальные и касательные напряжения, действующие в точке А (Рис.9.17б).

3. Определяем главные напряжения в точке А:

МПа;

МПа.

Для проверки используем условие инвариантности (9.16):

;.

Направление главных напряжений найдем, используя выражения (9.20):

;;

;.

Для проверки правильности решения сложим абсолютные величины углов и. Так как главные оси взаимно перпендикулярны, в сумме должен получиться угол 90⁰:

.

Решение выполнено верно. Отложим найденные углы на роисунке (Рис.9.18) и проставим значения главных напряжений.

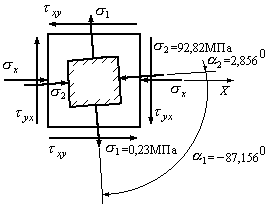
Рис.9.18