
- •Тема 9 основы теории напряженного и деформированного состояния
- •9.3.Плоское напряженное состояние
- •9.3.1. Вывод формул для напряжений на наклонных площадках
- •9.3.2. Вычисление величин главных напряжений и определение положения главных площадок
- •9.3.3. Экстремальные касательные напряжения
- •9.3.4. Примеры исследования плоского напряженного состояния в точке
- •9.4. Объемное напряженное состояние
- •9.4.1. Понятие о тензоре напряжений. Экстремальные касательные напряжения
- •9.4.2. Напряжения на произвольно наклоненных площадках
- •9.4.3. Октаэдрических напряжения. Понятие об интенсивности напряжений
- •9.5. Деформированное состояние в точке
- •9.5.1. Понятие о тензоре и девиаторе тензора деформаций. Главные линейные деформации
- •9.5.2. Закон Гука при плоском и объемном напряженном состоянии
- •9.5.3.Объемная деформация. Объемный закон Гука
- •9.6. Тесты к теме “Основы теории напряженного и деформированного состояния”
9.3.2. Вычисление величин главных напряжений и определение положения главных площадок
Исследуем выражение для нормальных
напряжений (9.14) на экстремум. Для этого
возьмем частную производную от напряжения
![]() по
по![]() и приравняем к нулю:
и приравняем к нулю:
![]() ,
(9.17)
,
(9.17)
где
![]() угол, который
составляет нормаль к рассматриваемой
площадке с положительным направлением
оси
угол, который
составляет нормаль к рассматриваемой
площадке с положительным направлением
оси![]() и при котором нормальное напряжение
и при котором нормальное напряжение![]() достигает наибольшего значения для
данной точки .
достигает наибольшего значения для
данной точки .
Выражение (9.17) представляет собой
величину касательного напряжения в
главной площадке
![]() .
Таким образом, касательное напряжение
в рассматриваемой площадке (
.
Таким образом, касательное напряжение
в рассматриваемой площадке (![]() )
равно нулю. Отсюда делаем вывод: площадка,
нормаль к которой составляет угол
)
равно нулю. Отсюда делаем вывод: площадка,
нормаль к которой составляет угол![]() с положительным направлением оси
с положительным направлением оси![]() ,
является главной площадкой.
,
является главной площадкой.
Приравнивая выражение в скобках формулы (9.17) нулю найдем тангенс двойного угла, определяющего наклон главных площадок:
![]() .
(9.18)
.
(9.18)
Выражение (9.18) дает два взаимно-перпендикулярных
направления с углами наклона
![]() и
и![]() ,
по которым действуют главные напряжения
(Рис.9.12).
,
по которым действуют главные напряжения
(Рис.9.12).
Для определения величин главных
напряжений подставим формулу (9.14)
![]() .
Вынося
.
Вынося![]() за скобку, получим:
за скобку, получим:
![]() .
(а)
.
(а)

Рис.9.12
Из тригонометрии известно:
 .
(б)
.
(б)
Знак
![]() поставлен потому, что косинусы углов
поставлен потому, что косинусы углов![]() и
и![]() имеют противоположные знаки. Подставляя
(9.18) в (б) и (а), получим:
имеют противоположные знаки. Подставляя
(9.18) в (б) и (а), получим:

![]() .
.
В этой
формуле знак “плюс”соответствует максимальному главному
напряжению![]() ,
а“минус”минимальному
,
а“минус”минимальному![]() .
Таким образом, окончательно имеем:
.
Таким образом, окончательно имеем:
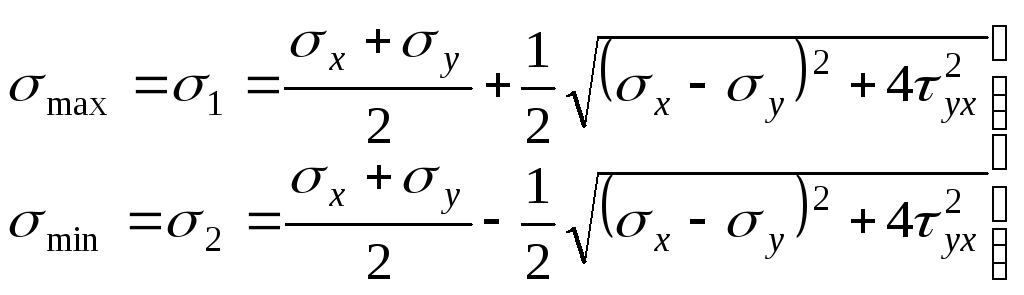 .(9.19)
.(9.19)
Из приведенного вывода следует, что при
любых исходных напряжениях
![]() в данной точке существует параллелепипед,
на гранях которого действуют только
нормальные напряжения.
в данной точке существует параллелепипед,
на гранях которого действуют только
нормальные напряжения.
Вернемся к формуле (9.18). Она дает два
главных направления, но не указывает,
в каком из них действует
![]() ,
а в каком
,
а в каком![]() .
Для решения этого вопроса надо было бы
исследовать знак второй производной
.
Для решения этого вопроса надо было бы
исследовать знак второй производной![]() при
при![]() и
и![]() .
Однако, можно решить эту задачу, используя
выражения, аналогичные тем, которые
применялись для определения направления
главных осей инерции в разделе“Геометрические
характеристики плоских фигур”:
.
Однако, можно решить эту задачу, используя
выражения, аналогичные тем, которые
применялись для определения направления
главных осей инерции в разделе“Геометрические
характеристики плоских фигур”:
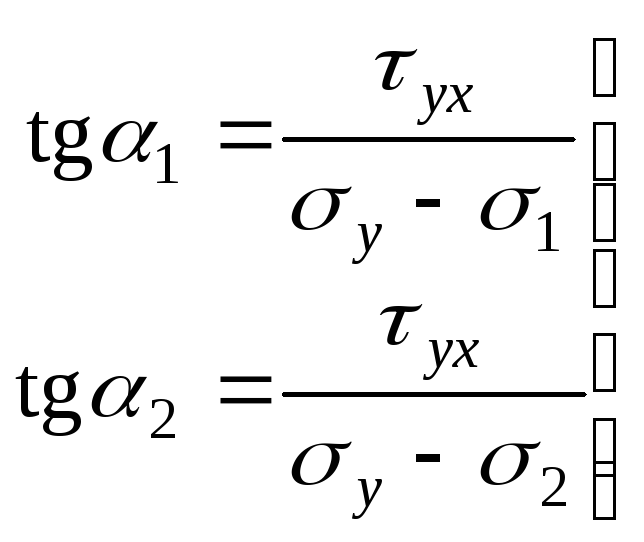 .
(9.20)
.
(9.20)
Здесь:
![]() угол, который
следует отложить от положительного
направления оси
угол, который
следует отложить от положительного
направления оси![]() до нормали к площадки, в которой действует
максимальное напряжение
до нормали к площадки, в которой действует
максимальное напряжение![]() ;
;![]() угол, который
следует отложить от положительного
направления оси
угол, который
следует отложить от положительного
направления оси![]() до нормали к площадки, в которой действует
минимальное напряжение
до нормали к площадки, в которой действует
минимальное напряжение![]() .
Положительный угол следует откладывать
против хода часовой стрелки, отрицательный
– по ходу часовой стрелки.
.
Положительный угол следует откладывать
против хода часовой стрелки, отрицательный
– по ходу часовой стрелки.
Для контроля правильности определения
положения главных площадок можно
использовать еще один способ, приведенный
в [2]. Исходя из того, что
с поворотом площадки в направлении
вектора касательных напряжений нормальное
напряжение на площадке алгебраически
возрастает, в работе[2]формулируется следующее правило:направление
![]() всегда проходит через две четверти осей
координат, в которых стрелки касательных
напряжений
всегда проходит через две четверти осей
координат, в которых стрелки касательных
напряжений![]() и
и![]() сходятся.
сходятся.
