9.3.Плоское напряженное состояние

Наиболее часто в задачах сопротивления материалов встречается плоское напряженное состояние: при кручении, изгибе, изгибе с кручением и т.д. Остановимся на нем подробнее.

9.3.1. Вывод формул для напряжений на наклонных площадках

Выделим из тела параллелепипед (Рис.9.8). Под действием сил, приложенных к его граням, параллелепипед находится в равновесии. Длины ребер параллелепипеда считаем бесконечно малыми и равными .

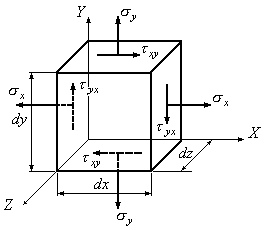
Рис.9.8

Рассмотрим наклонные площадки, перпендикулярные незагруженным граням параллелепипеда. Разрежем элементарный параллелепипед, изображенный на рис.9.8 , наклонным сечением, перпендикулярным плоскости , выделив из него элементарную треугольную призму (Рис.9.9а).

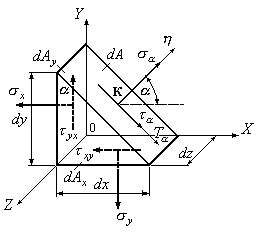
Рис.9.9

Наклон площадки с искомыми напряжениями будем определять углом , который образует внешняя нормаль к этой площадке с осью. Из рис.9.9 следует, что

(9.6)

Система сил, приведенная на рис.9.9, является плоской произвольной системой. Равновесие такой системы сил описывается тремя независимыми уравнениями. Составим эти уравнения.

. (9.7)

Откуда:

. (9.8)

Выражение (9.8) представляет собой закон парности касательных напряжений: касательные напряжения, действующие на двух любых взаимно перпендикулярных площадках, равны по величине и противоположны по знаку.

При плоском напряженном состоянии возможны лишь два варианта действия касательных напряжений (Рис.9.10).

Рис.9.10

Для определения напряжений на наклонной площадке спроектируем силы, действующие на призму (Рис.9.9) на оси и. Получим:

; (9.9)

. (9.10)

Подставляя в (9.9)-(9.10) вместо ииз выражения (9.6), сократим все слагаемые на. Далее, учитывая, что согласно (9.8), аи, находим:

; (9.11)

. (9.12)

Представим формулу (9.9) в несколько ином виде, используя известные из тригонометрии равенства:

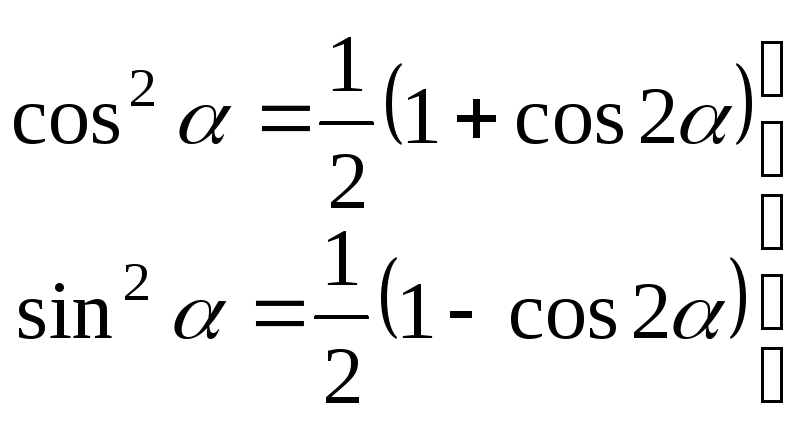. (9.13)

Подставляя (9.13) в (9.11), получаем:

. (9.14)

Выясним связь между нормальными напряжениями и, действующими на двух взаимно перпендикулярных площадках (Рис.9.11).

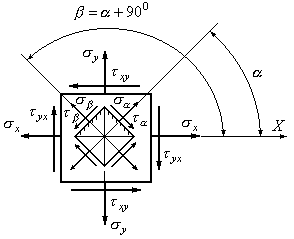
Рис.9.11

Напряжение определяется по формуле (9.14). Напряжениеполучим, если в эту формулу подставим:

или

. (9.15)

Складывая (9.14) и (9.15), приходим к выводу:

. (9.16)

Выражение (9.16) получило названия условия инвариантности суммы нормальных напряжений, действующих по двум взаимно перпендикулярным площадкам: в данной точке алгебраическая сумма нормальных напряжений, действующих по любым двум взаимно перпендикулярным площадкам, есть величина постоянная. Это условие используют для проверки правильности решения задач при исследовании напряженного состояния в точке.