1)Способы задания прямой на плоскости.

основные способы, которыми можно задать конкретную прямую на плоскости

Во-первых, прямую можно задать, указав две точки на плоскости.

Действительно, из аксиомы, рассмотренной в первом пункте этой статьи, мы знаем, что через две точки проходит прямая, и притом только одна.

Если в прямоугольной системе координат на плоскости указаны координаты двух несовпадающих точек, то есть возможность записать уравнение прямой, проходящей через две заданные точки.

Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. Этот способ справедлив, так как через данную точку плоскости проходит единственная прямая, параллельная заданной прямой. Доказательство этого факта проводилось на уроках геометрии в средней школе.

Если прямую на плоскости задать таким способом относительно введенной прямоугольной декартовой системы координат, то есть возможность составить ее уравнение.

В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор.

Если прямая линия задана в прямоугольной системе координат таким способом, то легко составить ее каноническое уравнение прямой на плоскости и параметрические уравнения прямой на плоскости.

Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Действительно, через заданную точку плоскости проходит единственная прямая, перпендикулярная данной прямой. Оставим этот факт без доказательства.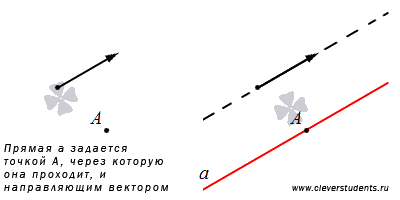

Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.

Если известны координаты точки, лежащей на заданной прямой, и координаты нормального вектора прямой, то есть возможность записать общее уравнение прямой.

3) Загальне рівняння прямої на площині та зміст його коефіцієнтів Розглянемо декартову систему координат . Покажемо, що рівняння,                                                   (1.1) де коефіцієнти__ довільні сталі, які одночасно не дорівнюють нулю, а вільний членможе набувати довільних значень із множини дійсних чисел, задає пряму лінію на площині. Прямі лінії позначатимемо великими латинськими буквами, наприклад,або.

1. Основні типи рівнянь прямої лінії на площині

1.1. Загальне рівняння прямої лінії на площині

Теорема 1.1. .Якщо на площині зафіксована довільна декартова система координат , то кожне рівняння першого степеня з двома зміннимитазадає щодо цієї системи координат пряму лінію.

Отже, загальне рівняння прямої ,                                                   (1.2)Рівняння прямої, яка проходить через точку і перпендикулярна до вектора .                                          (1.3) У рівняннях (1.2) та (1.3) векторназиваєтьсянормальним вектором прямої.

Рис. 1. Геометрична інтерпретація рівняння прямої лінії, що задається нормальним вектором

1.2. Неповні рівняння прямої лінії

Загальне рівняння прямої лінії на площині (1.2) назвемо повним, якщо всі коефіцієнти тавідмінні від нуля. Якщо хоча б один коефіцієнт у рівнянні (1.2) дорівнює нулю, то таке рівняння назвемонеповним.