
- •2) Действия над матрицами
- •4) Основні поняття визначників
- •5) Властивості визначників
- •7) Основні поняття слр
- •9) Розв'язок систем лiнiйних рівнянь методом Гауса.
- •8) Розв'язок слр за допомогою правила Крамера.
- •10) Розв'язок систем лiнiйних рівнянь матричним методом.
- •11) Основні поняття векторів
- •12. Лiнiйнi дiї з векторами у координатній формі
- •13. Скалярним добутком векторів:
- •14 Векторний та мішаний добутки двох векторів
- •1)Способы задания прямой на плоскости.
- •2) Основні види рівнянь прямої на площині
- •5) Загальне рівняння ліній другого порядку
- •13) Взаємне розташування двох прямих у просторі
- •14) Взаємне розташування прямої та площини у просторі
- •15) Функції
- •16) Границя функції
- •17) Бесконечно малые величины
- •18)Бесконечно большие величины
- •19) Первый замечательный предел
- •20) Второй замечательный предел
- •22) Неперервність функції
- •21) Розкриття невизначеностей
12. Лiнiйнi дiї з векторами у координатній формі
Колінеарність: Вектори є колінеарними тоді і тільки тоді, коли їхній векторний добуток дорівнює нулю.
Рівність
векторів: Нехай ![]() i
i![]() —
два вектори площини (або простору).
Кажуть, що вектор |
—
два вектори площини (або простору).
Кажуть, що вектор |![]() |
дорівнює вектору
|
дорівнює вектору![]() ,
і записують
,
і записують![]() =
=![]() ,
якщо:
1)довжина відрізка AB дорівнює
довжині відрізка CD;
2)променіAB
i CD однаково напрямлені.
,
якщо:
1)довжина відрізка AB дорівнює
довжині відрізка CD;
2)променіAB
i CD однаково напрямлені.
Лiнiйнi дiї з векторами у координатній формі :
Додаваня векторів
Правило
трикутника:
Сумою двох векторів
 називається вектор
називається вектор ,
який з’єднує початок вектора
,
який з’єднує початок вектора з кінцем вектора
з кінцем вектора (початок вектора
(початок вектора співпадає з кінцем вектора
співпадає з кінцем вектора ).
).
Суму
двох векторів можна знайти і за правилом
паралелограма:
якщо вектори
 прикладені до спільного початку, то їх
сумою є вектор
прикладені до спільного початку, то їх
сумою є вектор ,
який співпадає з діагоналлю паралелограма,
побудованого на векторах
,
який співпадає з діагоналлю паралелограма,
побудованого на векторах ,
і який виходить із спільного початку.
,
і який виходить із спільного початку.
Якщо є більше двох векторів, то для знаходженням їх суми використовують правило многокутника.
Віднімання векторів
Різницею
двох векторів
 називається вектор
називається вектор ,
сума якого з вектором
,
сума якого з вектором дорівнює вектору
дорівнює вектору .
.
Початок
вектора
 є кінцем вектора
є кінцем вектора ,
який віднімається. Кінець вектора
,
який віднімається. Кінець вектора співпадає з кінцем вектора
співпадає з кінцем вектора ,
від якого віднімають вектор
,
від якого віднімають вектор .
.
У
паралелограма, який побудовано на двох
векторах
 ,
одна діагональ - сума цих векторів, а
друга – їх різниця
,
одна діагональ - сума цих векторів, а
друга – їх різниця
Множення вектора на число
Добутком
ненульового вектора
 на
число k0
наз. вектор k
на
число k0
наз. вектор k .
.
Вектор
k має довжину
має довжину ,
він співнаправлений (має однаковий
напрям) з вектором
,
він співнаправлений (має однаковий
напрям) з вектором ,
якщо k>0 та протилежно направлений
вектору
,
якщо k>0 та протилежно направлений
вектору ,
якщо k<0.
,
якщо k<0.
13. Скалярним добутком векторів:
Скалярним
добутком
двох ненульових векторів
 називається число, яке дорівнює добутку
довжин цих векторів на косинус кута
між ними:
називається число, яке дорівнює добутку
довжин цих векторів на косинус кута
між ними:
Якщо
вектор
 має координати (х1,
y1),
а вектор
має координати (х1,
y1),
а вектор
 координати (х2,y2),
то:
координати (х2,y2),
то:

Наслідок
І.
 ;
ІІ.
Якщо
;
ІІ.
Якщо
 ,
то
,
то .
.
Властивості
1. Комутативність ![]() .
2. Лінійність
за кожним співмножником
.
2. Лінійність
за кожним співмножником ![]() ,де
,де ![]() –
довільне дійсне число.
3. Дистрибутивність
щодо додавання
–
довільне дійсне число.
3. Дистрибутивність
щодо додавання ![]() .
4. Скалярний
добуток векторів
.
4. Скалярний
добуток векторів ![]() та
та![]() дорівнює
нулю тоді і лише тоді, коли вектори
ортогональні або один із них дорівнює
нуль-вектору
дорівнює
нулю тоді і лише тоді, коли вектори
ортогональні або один із них дорівнює
нуль-вектору
![]() ,
або
,
або ![]() ,
або
,
або![]() .
.
Координати алгебраїчної суми скінченної кількості векторів дорівнюють такій же алгебраїчній сумі відповідних координат цих векторів.
Обчислення кута міждвома векторами.
За
означенням скалярного добутку
 .
.
Отже,
якщо
 ,
то
,
то

тобто,
косинус кута між
ненульовими векторами
 дорівнює скалярному добутку цих
векторів, поділеному на добуток їхніх
довжин.
дорівнює скалярному добутку цих
векторів, поділеному на добуток їхніх
довжин.
Нехай
у просторі маємо прямокутну декартову
систему координат, і нехай задано
вектори
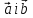 задані своїми координатами
задані своїми координатами i
i .
Тоді як відомо
.
Тоді як відомо
 ,
,
 ,
, ,
дістанемо формулу
,
дістанемо формулу

Ця
формула дає змогу обчислити косинус
кута між векторами
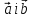 за
координатами цих векторів.
за
координатами цих векторів.
Проекція
вектора ![]() на
вісь
на
вісь![]() дорівнює
добутку довжини цього вектора на косинус
кута
дорівнює
добутку довжини цього вектора на косинус
кута ![]() між
вектором і віссю
між
вектором і віссю![]() :
:
пр![]()
![]()
Проекція
на вісь ![]() суми
векторів дорівнює алгебраїчній сумі
проекцій на вісь
суми
векторів дорівнює алгебраїчній сумі
проекцій на вісь![]() векторів-доданків:пр
векторів-доданків:пр![]()
![]()
Проекція
на вісь ![]() добутку
вектора
добутку
вектора![]() на
скаляр
на
скаляр![]() дорівнює
добуткові цього ж скаляра на проекцію
вектора на вісь
дорівнює
добуткові цього ж скаляра на проекцію
вектора на вісь![]() :
:
![]()
