1. Основні поняття матриць

Матриця- сукупність чисел, розміщених у вигляді прямокутної таблиці розміром m*n, де m - кількість рядків, n - кількість стовпчиків.

Матриці A=(a_ij) та B=(b_ij) називаються рівними (однаковими), якщо вони мають однакову кількість рядків та стовпців і всі їхні елементи, розташовані на однакових місцях, є рівними (тобто a_ij=b_ij для всіх значень i та j).

Матриця називається квадратною, якщо кількість її рядків співпадає із кількістю стовпців (n=m).

Квадратна матриця у якої всі елементи, які знаходяться за головною діагоналлю = 0, наз. діагональною.

Квадратна матриця E=(e_ij) називається одиничною, якщо

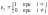
Матриця O називається нульовою, якщо всі її елементи є нулями:

Матриця, що складаєтьсь з 1 рядка, або 1 стовпчика наз. Вектор-рядком, або вектор-стовпчиком.

Матриця у якої всі елементи розміщені над(під) головною діагоналлю = 0 наз. трикутною.

2) Действия над матрицами

1) умножение матрицы на число

Что бы умножить матрицу на число, нужно умножить все элементы матрицы на это число

(-1)*А – противоположная матрица

2) сложение матриц

Суммой двух матриц А и В одинакового размера наз. матрица С, элементы которой равны сумме соответствующих элементов А и В.

3) умножение матриц

Если кол. столбцов 1 матрицы равняется кол. строк второй(2*2 2*3), то по правилу: строка на столбец.

Две матрицы А и В наз. перестановочными, если А*В=В*А

4) транспонирование матрицы

Матрица полученная из матрицы А заменой каждой строки столбцом с тем же номером.( A^T)

A^Т =А - симметричная

3. Обратная матрица

Обра́тная ма́трица — такая матрицаA⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицуE:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. 

Метод вычисления обратной матрицы:

1. Вычислить определитель данной матрицы. Если, то обратной матрицы не существует (матрицаА вырожденная).

2. Составить матрицу из алгебраических дополненийэлементов матрицыА.

3. Транспонируя матрицу , получить присоединенную матрицу.

4. Найти обратную матрицу , разделив все элементы присоединенной матрицы на определитель 

4) Основні поняття визначників

Число яке ставиться у відповідність кожної квадратної матриці наз. визначником(детермінантом). detA=|A|

Визначником матриці другого порядку

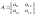наз. число

Визначником матриці третього порядку наз.  число D(A)=

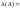
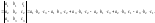
Мінором M_ij елемента a_ij визначн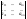ика називається визначник розміру(n-1)×(n-1) , який утворюється з визначника 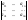викреслюваннямi-го рядка та j-го стовпця.

Алгебраїчним доповненням A_ij елемента a_ij називається його мінор, узятий з відповідним знаком

Для визначника довільного порядку виконується така

Теорема. Визначник дорівнює сумі добутків елементів довільного рядка (стовпця) на алгебраїчні доповнення цих елементів.

= a₁₁A₁₁+a₁₂A₁₂+…+a_1nA_1n

Ранг матриці – це кількість не нульових рядків верхньої трикутної матриці.

5) Властивості визначників

1.   Визначник не зміниться, якщо його рядки замінити відповідними стовпцями:

.

Ця властивість указує на рівноправність рядків і стовпців визначника.

2.  Визначник змінить знак на протилежний, якщо переставити місцями два рядки (два стовпці). Наприклад,

.

3.   Якщо всі елементи рядка (стовпця) дорівнюють нулю, то визначник дорівнює нулю.

4.   Визначник з двома однаковими рядками (стовпцями) дорівнює нулю.

5.   Спільний множник усіх елементів рядка (стовпця) можна винести за знак визначника.

.

6.   Визначник, який містить два пропорційні рядки (стовпці), дорівнює нулю.

.

7.   Якщо елементи деякого рядка (стовпця) є сумою двох доданків, то визначник дорівнює сумі двох визначників.

.

8.   Якщо до елементів будь-якого рядка (стовпця) визначника додати відповідні елементи іншого рядка (стовпця), помножені на одне й те саме число, то значення визначника не зміниться.