Якщо мова йдеться про промислове виготовлення одягу, у цьому випадку неможливо врахувати всі без винятку розмірні ознаки, тим паче для кожної окремої особи. Промисловці вимушені користуватися деякими узагальненими ознаками і залежностями, що у найбільшій мірі характеризують тіло людини. Тут виникають питання наступного плану. Які розмірні ознаки треба виділити як основні? Для промисловості їх повинно бути якомога менше. Яке співвідношення між основними та додатковими розмірними ознаками? Скільки відсотків одягу для різних розмірних ознак треба випускати, щоб найбільшим чином задовольнити споживача.

У якості споживача у цьому разі може виступати все населення. Природно, що неможливо дослідити кожного мешканця, який до того ж можливо й не збирається сьогодні бути споживачем. Відповідь на поставлені питання дають методи статистичного аналізу, який дозволяє дослідити поставлені питання для порівняно невеликої групи.

Питання про розмір групи споживачів, яких треба дослідити, залишається досить складним і не завжди є обґрунтованим. У деяких джерелах стверджується, що кількість осіб у дослідній групі не може бути менша тридцяти, але більшість наполягає на кількості не менше ста. Схиляючись скоріше до більшої кількості осіб, у той же час усвідомлюємо, що у випадку навчальної задачі вона може бути зменшена.

Для подальших дій будемо паралельно з описанням дій по статистичній обробці результатів вимірювань ілюструвати їх конкретними прикладами.

Домовляємося про сто випробувань, результати яких розміщуємо у таблиці. Нехай мова йде про один з основних розмірних ознак (обхват грудей). Підкреслюємо, що розміри взяті умовні.

Таблиця 1

Розмірна ознака, виміряна для ста осіб

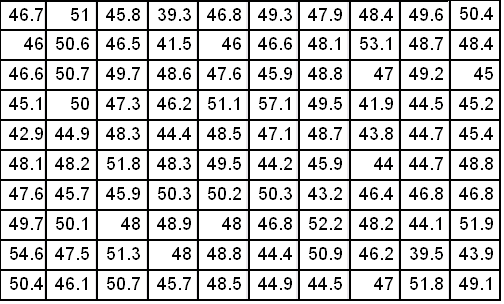
Наша перша мета – знайти закономірність розподілення цієї розмірної ознаки і розширити її на всіх споживачів, яких теоретично може бути без кінцева кількість.

Перший крок у цьому напряму – побудова гістограми розподілення частот, з якими зустрічаються різні розміри. Для цього вибираємо мінімальний визначений розмір. Для розгляданої вибірки це 39,3. Максимальний розмір 57,2. (Ще раз нагадуємо, що приведені розміри – умовні). Для формування гістограми наблизимо ці розміри до цілих значень

X_min=38, X_max=58.

Таким чином, досліджуваний інтервал розмірів 38<X<58. Розіб’ємо цей інтервал на певну кількість окремих інтервалів. Слід відзначити, що бажаним є більша кількість інтервалів. Вважаючи досить великий обсяг даних, для даного випадку можна взяти досить логічне розподілення на десять інтервалів по 2 см. У випадку меншої кількості результатів, кількість інтервалів відповідно треба брати меншою.

Для кожного інтервалу з даних таблиці 1 рахуємо кількість даних, що попадають в цей інтервал. Означимо цю кількість n_i. Цю окрему кількість у кожному випадку ділимо на загальну кількість вимірювань (у даному випадку на 100). Одержуємо густину частот попадання розмірів у заданий інтервал.

Результати заносимо у таблицю

Таблиця 2

Частоти попадання розмірів у заданий інтервал

ΔX	38-40	40-42	42-44	44-46	46-48	48-50	50-52	52-54	54-56	56-58
ni	2	2	4	20	23	27	18	2	1	1
Pi	0,02	0,02	0,04	0,2	0,23	0,27	0,18	0,02	0,01	0,01

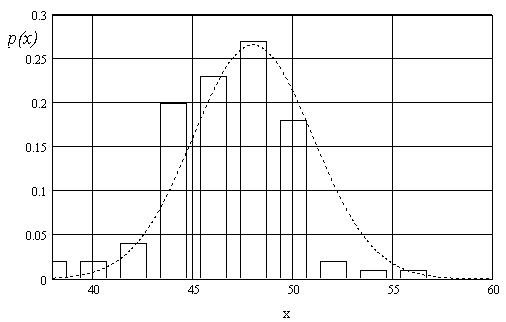
Будуємо гістограму, що уявляє з себе ступінчастий графік залежності густин від розмірів.

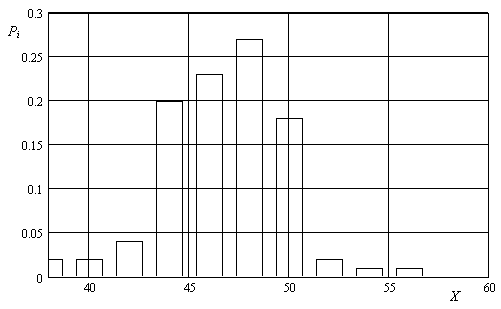
Для ілюстрації приведемо також приклад розподілення даної вибірки на п’ять інтервалів.

Таблиця 3

Частоти попадання розмірів у заданий інтервал для п’яти інтервалів

ΔX	38-42	42-46	46-50	50-54	54-58
ni	4	27	48	19	2
Pi	0,04	0,27	0,48	0,19	0,02

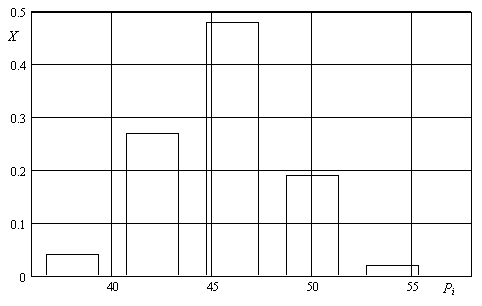
Після побудови гістограм по всім або деяким розмірним ознакам треба з’ясувати закон розподілення випадкової величини, якою виступає розмірна ознака в інтервалі розмірів, що досліджуються.

Наведемо основні типи розподілень, що запропоновані різними дослідниками для описання густин випадкових величин.

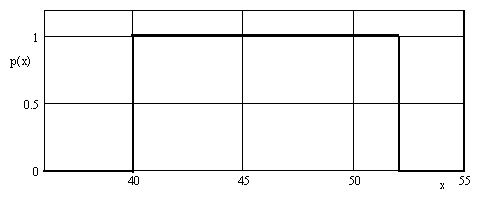
Рівномірне розподілення може бути математично описано, як

,

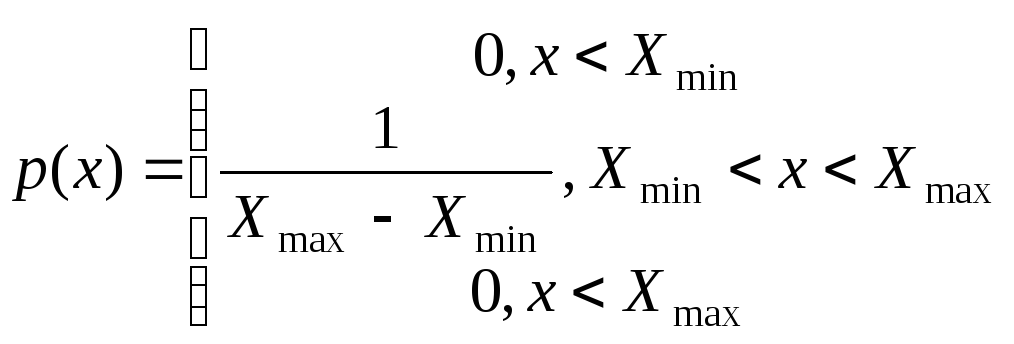що графічно може бути зображено на рис.

Нормальне розподілення математично записується, як

,

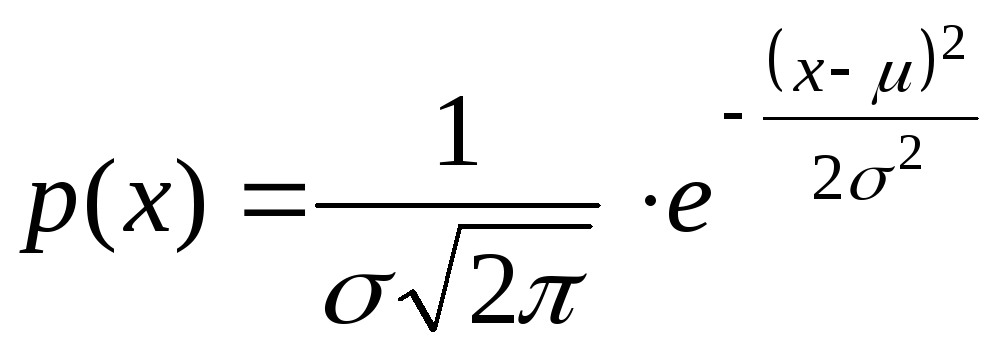Де - середнє значення (математичне очікування),

• середньоквадратичне відхилення,

• число пи (3,1415)

Графік залежності для нормального розподілення має вигляд.

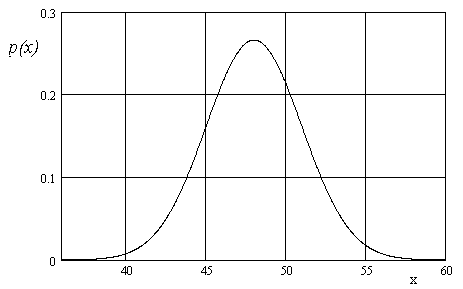
Більшість подальших дій засновано на положенні про нормальне розподілення випадкових величин.

Наведемо ще деякі розподілення

Основні характеристики так званого гамма розподілення визначаються наступним чином.

Центр розподілення (середнє значення) визначається з експерименту

.

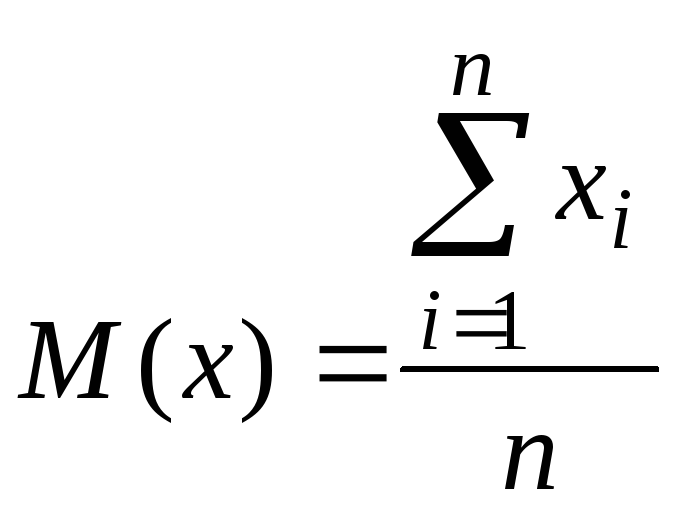Дисперсія для ряду випробувань визначається за формулою

.

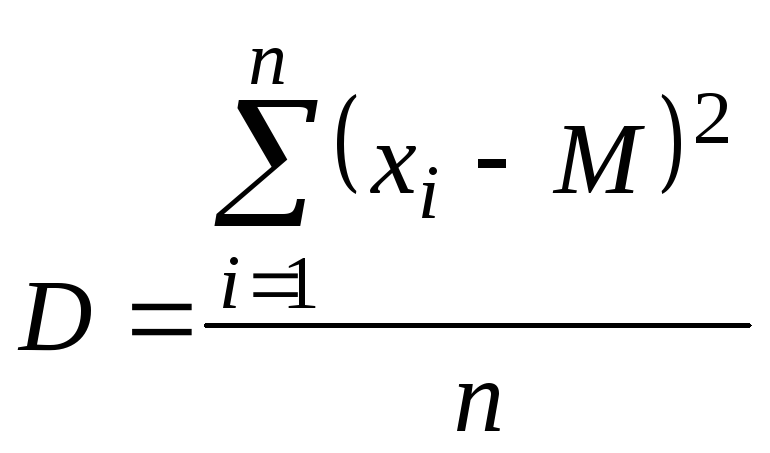Гамма розподілення має вигляд

,

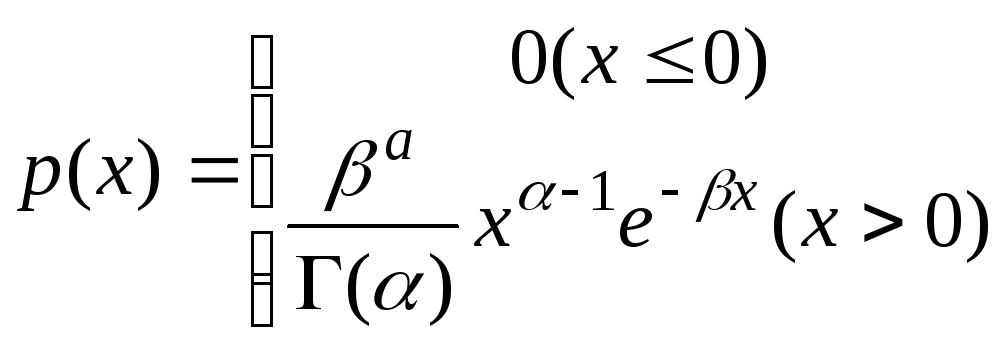де Г(α) –гамма – функція, визначається, як

Повна ймовірність попадання в проміжок до границі

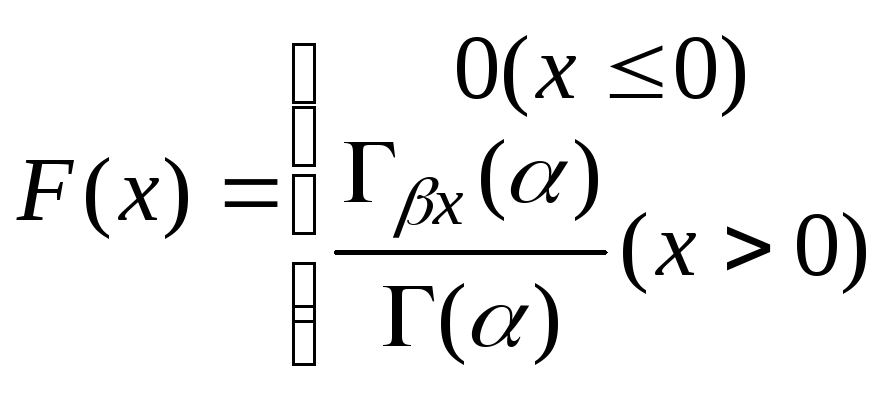, де

Г_βх(α) –неповна гамма – функція, визначається, як

Для гамма розподілення мають місце залежності

, .

Звідки можна знайти параметри гамма розподілення

, .

Зовнішній вигляд гамма розподілення

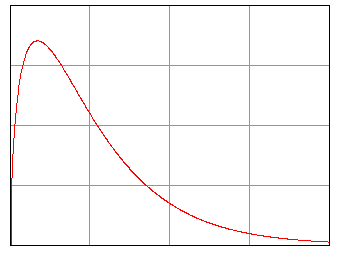
Гамма-розподілення ймовірностей

Якщо прийняти нормальний закон розподілення розмірної ознаки по групі споживачів, то його характеристики можна прийняти наступним чином. Математичне очікування (середнє значення) знаходиться як

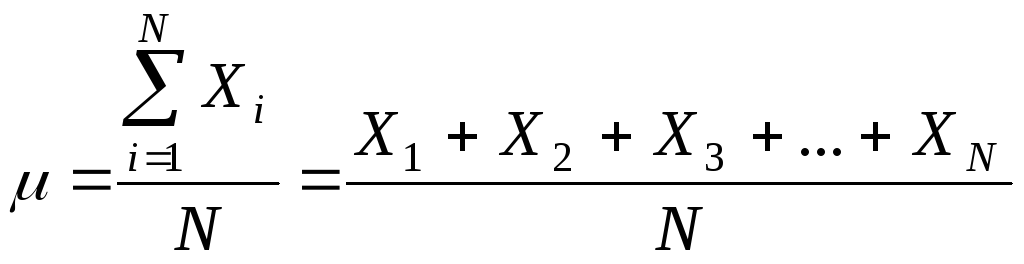
Дисперсія розраховується за формулою

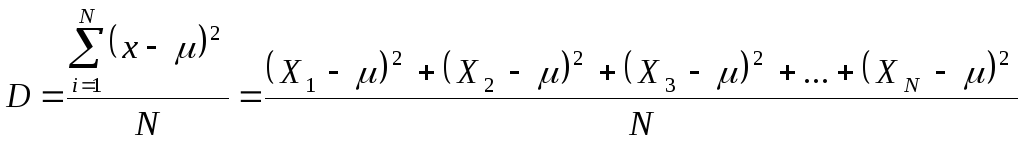
Середньоквадратичне відхилення знаходиться за формулою

Природно, що при сучасному розвитку комп’ютерної техніки було б нераціонально використовувати формули для ручного розрахунку. Для обробки статистичних даних зараз є досить багато програм, що значно прискорюють обробку даних.

Наприклад для використання програми Exсel, що є стандартною програмою Microsoft Office дані, одержані в результаті вимірювання заносяться в таблицю, наприклад у такому вигляді (рис.)

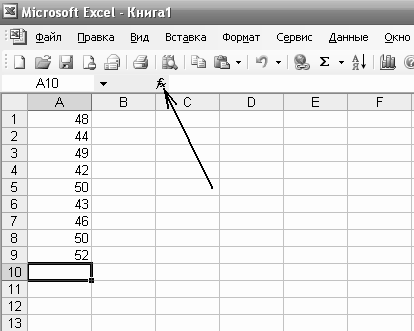
Якщо мова йде про знаходження математичного очікування, то тиснемо на прямокутничок, де ми бажаємо одержати наше значення (виділений товстими лініями на малюнку). Після чого натиснути кнопку функції f(x), вказану стрілочкою. У віконці, що з’явиться треба обрати функцію СРЗНАЧ. Після вводу цієї функції з’явиться віконце рис.

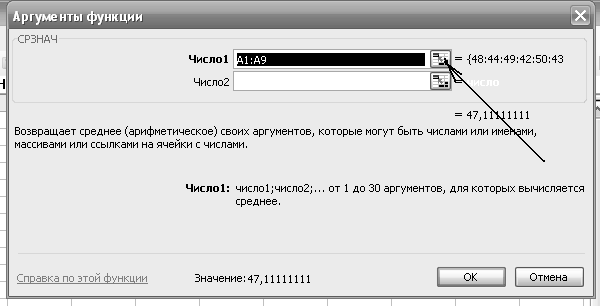
Звичайно у верхній строчці (там де написано «Число1») з’являється пропозиція для яких чисел виконується дія. У даному випадку від прямокутників в таблиці з координатами від А1 до А9. Якщо у нас інша думка, тиснемо на кнопку біля цієї строчки, підводимо курсор під перше число, тиснемо кнопку миші і виділяємо числа, середнє значення яких треба знайти. Після цього натиснути кнопку ОК. В запропонованому спочатку прямокутнику таблиці з’явиться число, що визначає математичне очікування (середнє значення) комплексу чисел. У даному випадку 47,11.

Для знаходження дисперсії виділяємо наступний прямокутник у таблиці. Тиснемо на кнопку функції, вводимо слово ДИСП. У віконці, що з’явилося (аналогічному рис.) тиснемо кнопку, що показана, виділяємо прямокутники від А1 до А9 (у більш складному випадку – всі ті, що досліджуємо, тиснемо кнопку ОК. Одержуємо дисперсію. У даному випадку 12,36. Середньоквадратичне відхилення визначає корінь квадратний з дисперсії. Його неважко знайти у наступній комірці. Тиснемо на неї. Потім на кнопку функції, де вводимо слово КОРЕНЬ. У віконці, що розгортається (подібне до рис. ) треба натиснути кнопку число, обрати число, з якого треба взяти корінь і натиснути кнопку ОК. Таким чином ми знайшли параметри нормального розподілення, що описують досліджену сукупність.

Для більш детального дослідження і особливо для візуалізації результатів зручніше використовувати більш пристосовані пакети, наприклад MathCAD. Першою задачею після його запуску повинно бути введення системи даних у вигляді вектора. Як правило в цьому середовищі вектори або матриці означаються великими літерами латинського алфавіту. Оператор присвоєння для вектор буде виглядати, як M:=. Після введення цього оператору треба натиснути на кнопку, що означена стрілкою на віконці «матриці» (рис.)

У віконці, що з’явилося, треба вибрати кількість строчок (наприклад, 10) і кількість стовпчиків ( у даному випадку 1), після чого заповнити вектор, що з’явиться (рис.)

Середнє значення визначається оператором mean(M), наприклад H:=mean(M), після чого можна ввести H= і одержати значення середнього. Для визначення середньоквадратичного відхилення можна використати оператор Stdev(M), наприклад S:= Stdev(M), після чого можна ввести S=. Для середовища MathCAD дуже зручним є те, що м миттєво можемо візуалізувати результати обчислень, наприклад у вигляді графіка. У випадку знайдених значень математичного очікування і середньоквадратичного відхилення можна записати функцію густини ймовірностей для нормального розподілення у вигляді p(x):=dnorm(x,H,S). Для побудови графіка на віконці побудови графіків (рис.) треба натиснути кнопку, що показана стрілкою

Після цього на екрані з’явиться «заготовка» майбутнього графіка у вигляді рис. . На місцях, що означені стрілочками встановлюємо: 1 – означення аргументу (х), 2 – нижня границя графіка, визначається мінімальним значенням, що очікується, наприклад 38, 3 – верхня границя, наприклад 56, 4 – означення функції, графік якої будується, у нашому випадку p(x). Після введення даних буде побудований графік нормального розподілення рис.

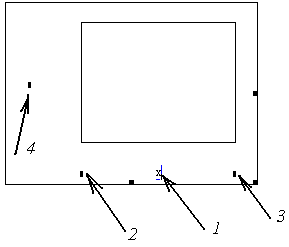
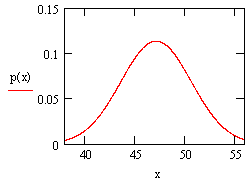
Одержаний графік можна «прикрасити», розтягнувши його курсором за кути, а також зобразити сітку, двічі клацнувши на графіку і поставивши відзначки у віконцях Grid Lines. Для використання цього графіка, визначимося з розмірами, які відповідають розміру від 43 до 45, тобто середньому розміру 44. Проведемо вертикальні лінії на графіку. Площа фігури, обмежена кривою розподілення та двома вертикальними лініями, визначає питому вагу споживачів, що потрапляють у даний розмір. Площина криволінійної фігури, як відомо, визначається інтегралом від функції з границями, що визначаються межами інтервалу

Функція нормального розподілення не інтегрується точно. Звичайно для визначення вказаного інтегралу використовували таблиці. В теперішній час використання комп’ютерної техніки значно спрощує цю задачу. В середовищі MathCAD для цього є стандартна процедура.

Для цього у віконці «обчислення» (рис. ) треба натиснути кнопку, означену стрілочкою

Після появи значка інтегралу на екрані треба ввести границі і функцію p(x) (вона була введена раніше). Одержимо вираз

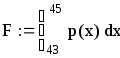
Одержимо F=0,15 або 15%.

Провівши аналогічні обчислення для інших проміжків, можна одержати питому вагу окремих розмірів споживачів певної групи.

Таблиця