Лабораторна робота №6. Розвязання задач динамічного програмування

Державний вищий навчальний заклад

«Українська академія банківської справи

Національного банку України»

Кафедра економічної кібернетики

ЕКОНОМІКО-МАТЕМАТИЧНІ МЕТОДИ І МОДЕЛІ

(ОПТИМІЗАЦІЙНІ МЕТОДИ І МОДЕЛІ).

РОЗВ’ЯЗАННЯ ЗАДАЧ ДИНАМІЧНОГО ПРОГРАМУВАННЯ

З ВИКОРИСТАННЯМ MS EXCEL

Методичні вказівки

щодо виконання лабораторної роботи

Для студентів всіх спеціальностей 6.030500

денної форми навчання

Суми – 2009

Лабораторна робота №6

«РОЗВ’ЯЗАННЯ ЗАДАЧ ДИНАМІЧНОГО ПРОГРАМУВАННЯ

З ВИКОРИСТАННЯМ MS EXCEL»

Мета роботи: набуття навичок вирішення задач динамічного програмування з використанням MS Excel

Зміст роботи: використовуючи принцип оптимальності (принцип Белмана) розв’язати задачу про оптимальну заміну обладнання за допомогою табличного процесору MS Excel.

Порядок виконання роботи:

1. Розв’язати задачу про оптимальну заміну обладнання з використанням MS Excel згідно номеру варіанту, наданого викладачем. Приклад розв’язання задачі про оптимальну заміну обладнання наведений в [1, с.169-173], [2, с.299-305]).

Постановка задачі:

При експлуатації виникає потреба заміни обладнання внаслідок зменшення прибутку з наступних причин:

1. Щорічний прибуток P_t від виробництва продукції із зростанням часу t зменшується як через фізичне старіння обладнання, що виготовляє цю продукцію, так і через зростаючі витрати на ремонт обладнання.

2. Експлуатаційні витрати EK_t з часом зростають через витрати на ремонт.

Мета підприємства – отримати максимальний прибуток, і тому коли цей прибуток зменшується, то підприємство повинно контролювати цей процес і визначити термін, коли обладнання треба замінити на нове.

Вважаємо, що нам відомі статистичні дані про щорічний дохід P_t від виробництва продукції на певному обладнанні; експлуатаційні витрати EK_t; вартість нового обладнання V₀ та залишкова вартість обладнання VZ_t віком t (див.табл.1). N – номер варіанту, наданий викладачем.

Таблиця 1

Статистичні дані експлуатації обладнання (V0=15N тис.грн, VZt = 0 тис.грн)
Характеристика обладнання, тис. грн.	Вік обладнання t
	0	1	2	3	4	5
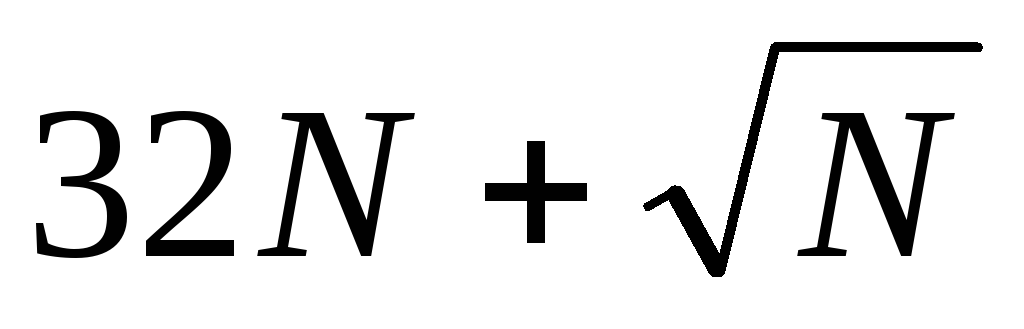
Pt, тис. грн.		28N+2	25N	21N	19N	17N
EKt, тис. грн.	2N	10N	12N	14N	16N	18N

2. Розв’язати задачу про оптимальний розподіл капіталовкладень з використанням MS Excel згідно номеру варіанту, наданого викладачем. Приклад розв’язання задачі про оптимальний розподіл капіталовкладень наведений в [1, с.166-169], [2, c.305-312], [3, с.365-373],).

Постановка задачі:

Галузь складається з n = 4 підприємств, Потрібно між ними розподілити ресурси x так, щоб = 100 ум.од. Значення прироcту випуску продукції на підприємствах g_i(x) в залежності від обсягів капіталовкладень x представлені в таблиці 2. Визначити оптимальний розподіл капіталовкладень, що дозволяє максимізувати загальний приріст випуску продукції.

Вимоги до оформлення звіту.

Звіт про проведення даної лабораторної роботи оформлюється наряду з іншими звітами цього курсу в окремому зошиті згідно встановлених вимог до оформлення звітів і містить:

• назву, тему, завдання, опис мети лабораторної роботи;

• вихідні дані варіанту;

• результати рішення задачі у вигляді аналітичного розв’язку, таблиці MS Excel;

• короткий опис технології вирішення задачі в MS Excel.

Контрольні питання:

1. Сформулюйте задачу динамічного програмування.

2. Назвіть методи розв’язування задач динамічного програмування.

3. Наведіть приклади економічних задач, що належать до класу задач динамічного програмування.

4. Сформулюйте принцип оптимальності Р. Белмана.

Перелік рекомендованої літератури:

1. Кутковецький В.Я. Дослідження операцій: навчальний посібник. – Миколаїв: Вид-во МДГУ ім. П. Могили, 2003. – 260 с.

2. Кучма М.І. Математичне програмування: приклади і задачі. Навчальний посібник. – Львів: «Новий Світ-2000», 2007. – 344 c.

3. Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. – К.: КНЕУ, 2003. – 452 с.

Таблиця 2

Варіант 1 Варіант 2

X	g1(x)	g2(x)	g3(x)	g4(x)			x	g1(x)	g2(x)	g3(x)	g4(x)
20	16	14	15	15			20	19	14	20	25
40	30	32	36	25			40	36	32	36	53
60	49	50	45	22			60	51	52	47	66
80	51	48	57	36			80	72	61	72	70
100	72	60	70	51			100	81	79	80	84

Варіант 3 Варіант 4

X	g1(x)	g2(x)	g3(x)	g4(x)			x	g1(x)	g2(x)	g3(x)	g4(x)
20	10	14	14	19			20	14	17	22	20
40	16	14	15	15			40	26	20	21	33
60	30	32	36	25			60	35	32	37	46
80	45	43	47	36			80	52	61	67	30
100	60	50	55	53			100	61	72	58	42

Варіант 5 Варіант 6

X	g1(x)	g2(x)	g3(x)	g4(x)			x	g1(x)	g2(x)	g3(x)	g4(x)
20	42	40	25	24			20	19	48	42	45
40	34	52	36	45			40	36	32	56	53
60	47	50	46	32			60	54	62	67	66
80	51	48	57	36			80	72	81	82	70
100	62	60	67	54			100	88	95	98	84

Варіант 7 Варіант 8

X	g1(x)	g2(x)	g3(x)	g4(x)			x	g1(x)	g2(x)	g3(x)	g4(x)
20	22	17	18	35			20	12	15	11	10
40	43	39	33	42			40	23	27	21	19
60	49	51	45	55			60	30	29	34	36
80	61	75	57	68			80	42	46	45	47
100	82	79	67	81			100	58	61	58	54

Варіант 9 Варіант 10

X	g1(x)	g2(x)	g3(x)	g4(x)			x	g1(x)	g2(x)	g3(x)	g4(x)
20	9	11	14	8			20	19	33	29	35
40	19	14	20	15			40	26	43	36	45
60	30	32	16	25			60	35	52	49	56
80	36	30	38	33			80	47	60	62	72
100	48	44	52	36			100	68	79	82	94

Варіант 11 Варіант 12

X	g1(x)	g2(x)	g3(x)	g4(x)			x	g1(x)	g2(x)	g3(x)	g4(x)
20	12	24	10	20			20	22	24	28	25
40	21	17	16	25			40	38	32	46	33
60	20	21	25	22			60	45	44	57	46
80	30	38	22	23			80	52	56	67	58
100	42	35	18	41			100	51	69	70	68

Варіант 13 Варіант 14

X	g1(x)	g2(x)	g3(x)	g4(x)			x	G1(x)	g2(x)	g3(x)	g4(x)
20	12	24	25	18			20	29	24	22	25
40	23	32	36	22			40	36	33	36	35
60	33	40	44	32			60	48	22	44	46
80	45	48	47	36			80	52	46	53	49
100	52	60	57	35			100	58	39	68	38

Варіант 15 Варіант 16

X	g1(x)	g2(x)	g3(x)	g4(x)			X	g1(x)	g2(x)	g3(x)	g4(x)
20	6	4	5	8			20	9	14	10	15
40	10	12	16	15			40	26	22	23	18
60	24	25	24	22			60	35	28	27	16
80	21	24	27	31			80	32	38	32	20
100	32	30	37	45			100	41	46	48	34