
- •Лекція 1 Тема: Скінченновимірні векторні простори
- •1. Поняття, приклади і найпростіші властивості векторного простору над полем
- •3. Ранг матриці
- •4. Базис і розмірність векторного простору
- •5. Координати вектора у векторному просторі. Розкладання вектора за базисом
- •2) Розкладемо вектор за базисом:
- •Розв’язуючи цю систему будь-яким способом, знайдемо , ,.
- •6. Ізоморфізм векторних просторів
- •7. Системи лінійних алгебраїчних рівнянь (загальна теорія)
- •Слар сумісна .
- •Слар має єдиний розв’язок
- •Слар має безліч розв’язків
- •8. Підпростори векторного простору
8. Підпростори векторного простору
Означення.
Непорожня
підмножина
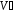 векторного простору
векторного простору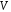 називаєтьсяпідпростором
простору
називаєтьсяпідпростором
простору
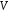 ,
якщо воно є векторним простором відносно
операцій, визначених в
,
якщо воно є векторним простором відносно
операцій, визначених в .
.
Це
означає, що множина
 задовольняє аксіомам векторного
простору, якщо додавати його елементи
і множити їх на числа з поля
задовольняє аксіомам векторного
простору, якщо додавати його елементи
і множити їх на числа з поля (над яким заданий векторний простір
(над яким заданий векторний простір )
так, як це визначено для елементів
простору
)
так, як це визначено для елементів
простору .
.
Теорема
(критерій підпростору). Непорожня
підмножина
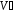 векторного простору
векторного простору є
підпростором простору
є
підпростором простору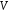 оді і тільки тоді, коли виконується
наступні умови:
оді і тільки тоді, коли виконується
наступні умови:
Якщо
 ,
то
,
то ;
;Якщо
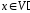 ,
,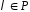 то
то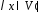 .
.
Кожний підпростір будь-якого векторного простору саме по собі є векторним простором. тому всі поняття, які були введені для просторів (розмірність, базис та ін.) розповсюджуються і на підпростори.
Теорема (про розмірність підпростору). Розмірність будь-якого підпростору векторного простору не більше розмірності простору.
Приклади підпросторів.
1)
Множина
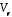 ,
яка містить тільки нульовий елемент
,
яка містить тільки нульовий елемент є підпростором будь-якого векторного
простору. Його називаютьнульовим
підпростором.
В нульовому підпросторі нема лінійно
незалежних систем векторів. Його базис
– порожня множина. Його розмірність
вважають нульовою.
є підпростором будь-якого векторного
простору. Його називаютьнульовим
підпростором.
В нульовому підпросторі нема лінійно
незалежних систем векторів. Його базис
– порожня множина. Його розмірність
вважають нульовою.
2)
Будь-який векторний простір
 є своїм підпростором.
є своїм підпростором.
Нульовий
підпростір
 і сам простір
і сам простір звичайно називаютьневласними
підпросторами.
звичайно називаютьневласними
підпросторами.
3)
В арифметичному числовому векторному
просторі
 множина
множина ,
, ,
векторів вигляду
,
векторів вигляду є підпростором.
є підпростором.
4)
Векторний простір многочленів з
коефіцієнтами з поля
 є підпростором векторного простору
функцій, неперервних на відрізку
є підпростором векторного простору
функцій, неперервних на відрізку ,
якщо многочлени вважати заданими на
відрізку
,
якщо многочлени вважати заданими на
відрізку .
.
5)
У векторному просторі
 геометричних векторів підпросторами
будуть вусі площини і всі прямі, що
проходять через початок координат.
геометричних векторів підпросторами
будуть вусі площини і всі прямі, що
проходять через початок координат.
6)
Лінійні оболонки є цікавим прикладом
підпростору. Нехай
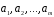 – довільна система векторів простору
– довільна система векторів простору .
Множина всіх векторів, які є лінійними
комбінаціями векторів системи
.
Множина всіх векторів, які є лінійними
комбінаціями векторів системи
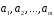 є підпростором простору
є підпростором простору
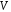 ,
який позначається
,
який позначається і називається лінійною оболонкою
векторів
і називається лінійною оболонкою
векторів ,
або підпростором, натягнутим на вектори
,
або підпростором, натягнутим на вектори .
.
