Практичне заняття № 1 Тема: Скінченновимірні векторні простори над полем

Мета заняття: Засвоїти поняття векторного простору над полем, методику визначення лінійної залежності та незалежності систем векторів, розв’язування систем лінійних алгебраїчних рівнянь загального виду.

Короткі теоретичні відомості.

1. Поняття векторного простору над полем

Нехай – непорожня множина елементів будь-якої природи, які будемо позначатиі нехай– деяке довільне числове поле, елементи якого будемо позначати. Визначимо в множиніоперацію додавання елементів: і операцію множення елемента на число з поля : .

Означення. Множина називаєтьсявекторним (лінійним) простором, якщо в визначені алгебраїчна операція додавання і операція множення на числа з поля, причому виконані наступні умови (аксіоми векторного простору):

1. – асоціативність додавання;

2. – комутативність додавання ;

3. :– існування нульового елемента ;

4. :– існування протилежного елемента;

5. – асоціативність множення на число;

6. .

7. – дистрибутивність відносно додавання чисел ;

8. – дистрибутивність відносно додавання елементів;

Елементи векторного простору називаються векторами, елемент називається нульовим вектором (нуль-вектором).

Найпростіші властивості векторного простору:

1) Єдиність нульового вектора. В векторному просторі існує єдиний нульовий вектор, тобто такий, що: . (аксіома 3)

2) Єдиність протилежного елемента. В векторному просторі для будь-якого вектора існує єдиний вектор такий, що . (аксіома 4)

3) Для будь-якого вектора .

4) Для будь-якого числа і.

5) Якщо добуток , то або, або.

6) Для будь-якого вектора елементє протилежним до.

2. Лінійна залежність системи векторів Означення. Лінійною комбінацією векторів векторного просторуназивається векторвигляду

.(1)

де – деякі числа з поля(коефіцієнти лінійної комбінації).Якщо вектор 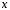записаний у вигляді (1), то кажуть, що вінрозкладений за системою векторів , або що він лінійно виражається через вектори .

Означення. Система векторів векторного просторуназиваєтьсялінійно залежною, якщо існують числа , які не всі водночас дорівнюють нулю (), такі що

(2)

Система векторів називаєтьсялінійно незалежною, якщо остання рівність виконується тільки в одному випадку, коли

Теорема (про лінійну залежність векторів). Вектори лінійно залежні тоді і тільки тоді, коли один з векторів цієї системи є лінійною комбінацією інших.

Теорема (про лінійну залежність системи векторів). Якщо деяка підсистема заданої системи векторів лінійно залежна, то і вся система векторів лінійно залежна.

3. Ранг матриці

Розглянемо довільну матрицю розмірності:

Будемо дивитися на рядки матриці як на вектори арифметичного числового векторного простору, а на саму матрицю – як на скінченну систему векторів.

Означення. Рангом матриці називається ранг системи рядків матриці.

З означення рангу системи векторів випливає, що ранг матриці дорівнює максимальному числу лінійно незалежних рядків. Позначається ранг матриці .

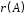Оскільки максимальна лінійно незалежна підсистема рядків матриці утворює базис системи всіх рядків, то такі рядки називають базисними рядками.

Властивості рангу матриці:

1. Ранг матриці не змінюється при її транспонуванні.

2. Ранг матриці не змінюється при множенні всіх елементів деякого рядка (стовпця) на ненульове число.

4. Ранг матриці не змінюється при елементарних перетвореннях рядків (стовпців).

Сформульовані властивості вказують можливий шлях обчислення рангу матриці: Щоб обчислити ранг матриці, треба спростити її за допомогою елементарних перетворень так, щоб висновок про ранг став очевидним.

(Елементарними перетвореннями матриці називаються такі перетворення:

1. переставлення двох рядків (стовпців);

2. множення рядка (стовпця) на довільне дійсне число, відмінне від 0 ;

3. додавання до одного рядка (стовпця) іншого рядка (стовпця) помноженого на довільне дійсне число;

4. викреслювання або дописування нульового рядка (стовпця).)