
- •Практичне заняття № 2 Тема:Лінійні оператори в векторних просторах
- •1. Лінійні оператори і матриці лінійних операторів
- •3. Детермінант мтариці.
- •4. Характеристичний та мінімальний многочлени матриці
- •5. Мінімальний многочлен вектора відносно матриці
- •6. Власний, інваріантний та циклічний підпростори лінійного оператора
- •Зміст практичного заняття
4. Характеристичний та мінімальний многочлени матриці
Нехай
 – квадратна матриця порядку
– квадратна матриця порядку над полем
над полем .
.
Означення.
Характеристичною матрицею матриці
 називається матриця
називається матриця

із
змінною
 ,
яка набуває будь-які числові значення.
,
яка набуває будь-які числові значення.
Означення.
Характеристичним многочленом матриці
 називається визначник характеристичної
матриці:
називається визначник характеристичної
матриці:
 ,
,
який
являє собою многочлен від змінної
 степеня
степеня .
Корені характеристичного многочлена
називаються характеристичними коренями
абохарактеристичними
числами матриці
.
Корені характеристичного многочлена
називаються характеристичними коренями
абохарактеристичними
числами матриці
 .
.
В
довільний многочлен
 замість
змінної
замість
змінної можна підставити квадратну матрицю
можна підставити квадратну матрицю порядку
порядку
 .
.
Означення.
Якщо
для заданої квадратної
матриці
 порядку
порядку
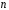
 ,
то
,
то називаєтьсяматричним
коренем многочлена
називаєтьсяматричним
коренем многочлена
 ,
а многочлен
,
а многочлен називаєтьсямногочленом,
що анулюється матрицею
називаєтьсямногочленом,
що анулюється матрицею
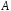 .
.
Має місце теорема.
Теорема (Гамільтона-Келі). Кожна матриця є коренем свого характеристичного многочлена.
Означення.
Мінімальним многочленом
матриці
 над полем
над полем називається нормований многочлен
називається нормований многочлен найменшого степеня, що анулюється
матрицею
найменшого степеня, що анулюється
матрицею .
.
Теорема
(про анулюючий многочлен).
Будь-який
многочлен, що
анулюється матрицею
 ,
ділиться без остачі на мінімальний
многочлен матриці
,
ділиться без остачі на мінімальний
многочлен матриці .
Зокрема, характеристичний многочлен
матриці
.
Зокрема, характеристичний многочлен
матриці ділиться без остачі на мінімальний
многочлен матриці
ділиться без остачі на мінімальний
многочлен матриці .
.
Наслідок.
Будь-який корінь мінімального многочлена
матриці
 є її характеристичним коренем.
є її характеристичним коренем.
Коренями
мінімального многочлена
 є
всі різні
корені характеристичного многочлена
є
всі різні
корені характеристичного многочлена
 причому, якщо
причому, якщо
 ,
,
то
 ,
,
де
 ,
, .
.
Існують наступні способи побудови мінімального многочлена:
Для побудови мінімального многочлена матриці
 для кожногохарактеристичного
кореня
для кожногохарактеристичного
кореня
 ,
, ,
складають матрицю
,
складають матрицю
 і підносять її до степенів
і підносять її до степенів
 доти, поки не буде виконана рівність
доти, поки не буде виконана рівність ,де
,де
 – ранг матриці
– ранг матриці
 ;
; – порядок матриці
– порядок матриці ;
;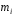 – кратність характеристичного кореня
– кратність характеристичного кореня матриці
матриці .
Найменше натуральне число
.
Найменше натуральне число ,
при якому виконується рівність
,
при якому виконується рівність ,
дає кратність
,
дає кратність кореня
кореня в мінімальному многочлені
в мінімальному многочлені матриці
матриці
 .
.За теоремою про анулюючий многочлен мінімальним многочленом може бути один з многочленів – дільників характеристичного многочлена. Треба перевірити, які з цих многочленів є анулюючими і вибрати з них многочлен мінімального степеня.
5. Мінімальний многочлен вектора відносно матриці
Нехай
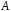 – квадратна матриця порядку
– квадратна матриця порядку над полем
над полем ,
, .
.
Означення.
Мінімальним многочленом вектора
 відносно матриці
відносно матриці
 називається нормований многочлен
називається нормований многочлен найменшого степеня, для якого
найменшого степеня, для якого .
.
Для
побудови мінімального многочлена
вектора
 відносно
матриці
відносно
матриці
 розглянемо
послідовність векторів
розглянемо
послідовність векторів
 . На кожному кроці
. На кожному кроці будемо перевіряти, чи є система отриманих
векторів лінійно незалежною. В силу
скінченновимірності простору
будемо перевіряти, чи є система отриманих
векторів лінійно незалежною. В силу
скінченновимірності простору знайдеться таке ціле число
знайдеться таке ціле число ,
, ,
що вектори
,
що вектори будуть лінійно незалежні, а вектор
будуть лінійно незалежні, а вектор буде лінійною комбінацією цих векторів
з коефіцієнтами з поля
буде лінійною комбінацією цих векторів
з коефіцієнтами з поля .
Інакше кажучи, знайдуться коефіцієнти,
не всі рівні нулю, що виконається
співвідношення
.
Інакше кажучи, знайдуться коефіцієнти,
не всі рівні нулю, що виконається
співвідношення .
Цьому співвідношенню відповідає
многочлен
.
Цьому співвідношенню відповідає
многочлен
 ,
,
який
залежить
від матриці
 та вектора
та вектора .
.
6. Власний, інваріантний та циклічний підпростори лінійного оператора
Нехай
лінійний оператор
 у векторному просторі
у векторному просторі над полем
над полем має в деякому базисі матрицю
має в деякому базисі матрицю .
.
Означення.
Власним вектором оператора
 називається такий ненульовий вектор
називається такий ненульовий вектор ,
який цим оператором переводиться в
пропорційний йому вектор
,
який цим оператором переводиться в
пропорційний йому вектор ,
тобто
,
тобто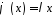 ,
де
,
де –
деяке число з поля
–
деяке число з поля ,
яке називаєтьсявласним
значенням оператора
,
яке називаєтьсявласним
значенням оператора
 .
.
Теорема.
Власними значеннями лінійного оператора
 ,
який діє у векторному просторі
,
який діє у векторному просторі над полем
над полем
 є характеристичні корені цього оператора,
які належать полю
є характеристичні корені цього оператора,
які належать полю .
.
Для
знаходження всіх власних значень
оператора
 з матрицею
з матрицею треба знайти всі характеристичні числа
матриці
треба знайти всі характеристичні числа
матриці і з них вибрати тільки ті, які належать
полю
і з них вибрати тільки ті, які належать
полю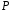 .
Для знаходження всіх власних векторів
оператора
.
Для знаходження всіх власних векторів
оператора з матрицею
з матрицею для кожного власного значення
для кожного власного значення треба знайти всі ненульові розв’язки
системи
треба знайти всі ненульові розв’язки
системи .
.
Теорема.
Множина
 власних векторів лінійного оператора
власних векторів лінійного оператора ,
які відповідають власному значенню
,
які відповідають власному значенню ,
разом з нульовим вектором утворює
лінійний підпростір векторного простору
,
разом з нульовим вектором утворює
лінійний підпростір векторного простору
 .
.
Означення.
Власним
підпростором, що відповідає власному
значенню оператора
 називається
підпростір
називається
підпростір
 ,
утворений власними векторами, які
відповідають власному значенню
,
утворений власними векторами, які
відповідають власному значенню
 .
.
За
означенням
 .
Якщо оператор
.
Якщо оператор взаданому
базисі має матрицю
взаданому
базисі має матрицю
 ,
то
,
то .
.
Власний
підпростір є окремим випадком інваріантного
підпростору лінійного оператора
 .
.
Означення.
Інваріантним
підпростором лінійного оператора
 називається такий підпростір
називається такий підпростір ,
що образом кожного вектора з
,
що образом кожного вектора з є вектор, який знову належить
є вектор, який знову належить ,
тобто
,
тобто
 .
.
Означення.
Циклічним
підпростором лінійного оператора
називається
інваріантний підпростір з базисом
виду
 .
Вектор
.
Вектор
 називаєтьсятвірним
вектором
циклічного підпростору.
називаєтьсятвірним
вектором
циклічного підпростору.
Мінімальний
многочлен такого підпростору має степінь
 ,
оскільки вектори
,
оскільки вектори обов’язково будуть лінійно залежними.
обов’язково будуть лінійно залежними.
