8.2 Довірчий інтервал для математичного сподівання при невідомій дисперсії

У багатьох випадках припущення про нормальний розподіл випадкової величини стає прийнятним прив цілому добре виправдовується при. Оцінкацілком придатна для застосування замість. Але все не так з дисперсією. Правомочність замінина вибіркову дисперсію

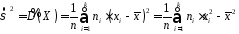
не обґрунтована навіть у вказаних випадках. При невеликому об'ємі вибірки, , закон розподілу оцінки дисперсії брати за нормальний невиправдано. Її розподіл слід апроксимувати розподілом хі-квадрат як суми квадратів центрованих величин (хі-квадрат розподіл збігається до нормального при числі доданків, що перевищує 30). Але це твердження обґрунтоване тільки тоді, коли випадкова величина Х розподілена нормально.

Розглянемо випадкові величини

(виправлену вибіркову дисперсію – незміщену оцінку дисперсії ) і

.

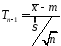Тоді випадкова величина має розподіл Стьюдента зстепенями вільності. Функція щільності розподілу цієї випадкової величини має вигляд

.

Розподіл Сьюдента симетричний, тому отримане співвідношення між точністю, надійністю оцінки і об’ємом вибірки зберігається. Виберемо число так, щоб виконувалась нерівність

.

З означення функції щільності розподілу Стьюдента, значення меж інтервалу для параметра можна записати як розв’язок інтегрального рівняння

.

Розв’язок цього інтегрального рівняння позначається 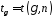і наводиться в статистичних таблицях.

Зауваження. Критичні точки розподілу Стьюдента можна обчислити

а) в Excel за формулою =СТЬЮДРАСПОБР(1-α; k), де α – рівень значущості (), k– число ступенів свободи.

а) в Mathcad за формулою qt(1–α/2; k), де α – рівень значущості, k – число ступенів свободи.

Приведемо нерівність до еквівалентного вигляду

або

.

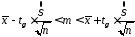Ця нерівність задає довірчий інтервал для математичного сподівання з надійністю: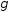

.

Приклад 2. В умовах прикладу 1 знайти довірчий інтервал для математичного сподівання з надійністю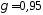, якщо дисперсія невідома.

Розв’язання. Об'єм вибірки . Середнє вибіркове значення. Обчислимо вибіркову дисперсію:

,

,

і виправлену вибіркову дисперсію :

.

Об'єм заданої вибірки достатньо великий, . Тому можна використовувати як розподіл Стьюдента, так і нормальний розподіл. Розглянемо обидва варіанти.

Варіант 1 (нормальний закон розподілу). Будемо припускати, що , а. За заданою надійністюзнайдемо за допомогою таблиці значень функції Лапласа, параметр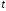: 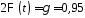, звідки,. Отримаємо довірчий інтервал для математичного сподівання

.

Проведемо обчислення і остаточно запишемо

.

Таким чином, інтервал покриває параметрз надійністюпри невідомій дисперсії.

Варіант 2 (закон розподілу Стьюдента). За заданою надійністю знайдемо за допомогою таблиці значень розподілуСтьюдента, параметр :.Отримаємо довірчий інтервал для математичного сподівання

.

Проведемо обчислення і остаточно запишемо

.

Таким чином, інтервал покриває параметрз надійністюпри невідомій дисперсії.

Можна помітити, що якщо значення близьке до, то довірчий інтервал, отриманий із застосуванням закону розподілу Стьюдента, буде ширшим, ніж довірчий інтервал, отриманий із застосуванням формул нормального розподілу, оскільки. Це пояснюється тим, що розподіл Стьюдента застосовується при вибірках малих об'ємів, що містять недостатній об'єм інформації.

Приклад 3. За даними спостережень випадкової величини , розподіленої нормально, знайти довірчий інтервал для математичного сподіванняз надійністю. Вибірка представлена таблицею.

Інтервали	(5;10)	(10;15)	(15;20)	(20;25)	(25;30)
Середини інтервалів 15	7,5	12,5	17,5	22,5	27,5	30
частоти	1	5	8	4	2

Розв’язання. Знайдемо об'єм вибірки, для чого підсумуємо вказані в таблиці частоти: . Оскільки об'єм вибірки невеликий, то застосування нормального закону розподілу приведе до невиправданого звуження довірчого інтервалу, тому використовуємо формули, отримані для розподілу Стьюдента. Обчислимо необхідні параметри:

.

.

,

.

.

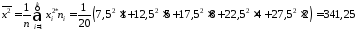За заданою надійністю знайдемо за допомогою таблиці значень розподілуСтьюдента, параметр :.Отримаємо довірчий інтервал для математичного сподівання

.

Проведемо обчислення і остаточно запишемо

.

Таким чином, інтервал покриває параметрз надійністюпри невідомій дисперсії.