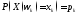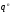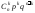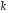- •Лекція № 10 Тема: Біноміальний, рівномірний і нормальний розподіл ймовірностей
- •1. Біноміальний розподіл ймовірностей
- •1.1. Розподіл Бернуллі
- •2. Рівномірний розподіл
- •2.1 Рівномірний дискретний розподіл
- •2.2 Рівномірний неперервний розподіл
- •3. Нормальний розподіл ймовірностей
- •4. Нормальне наближення
- •5. Розподіли, пов’язані з нормальним
- •1) Розподіл 2 (хі-квадрат)
- •2) Розподіл Стьюдента (-розподіл)
- •6. Оцінки параметрів розподілу випадкових величин
- •7. Оцінки параметрів біноміального розподілу
- •8. Оцінки параметрів нормального розподілу
- •8.1 Довірчий інтервал для математичного сподівання при відомій дисперсії
- •8.2 Довірчий інтервал для математичного сподівання при невідомій дисперсії
- •8.3. Довірчий інтервал для дисперсії при відомому математичному сподіванні
- •8.4. Довірчий інтервал для дисперсії при невідомому математичному сподіванні
- •8.5. Довірчий інтервал для середнього квадратичного відхилення
Ю.Д.Жданова. Лекції з ВГПМ. М3 Вибрані глави ТЙіМС. Лекція № 10
Лекція № 10 Тема: Біноміальний, рівномірний і нормальний розподіл ймовірностей
План лекції:
1. Біноміальний розподіл ймовірностей.
2. Рівномірний розподіл ймовірностей.
3. Нормальний розподіл ймовірностей.
4. Нормальне наближення.
5. Розподіли, пов’язані з нормальним.
6. Оцінки параметрів розподілу випадкових величин.
7. Оцінки параметрів біноміального розподілу.
8. Оцінки параметрів нормального розподілу.
1. Біноміальний розподіл ймовірностей
Припустимо,
що проводиться серія незалежних
випробувань, в кожному з яких може
відбутися подія
 з однією і тією ж, але невідомою нам
ймовірністю
з однією і тією ж, але невідомою нам
ймовірністю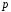 .
Причому ймовірність появи події
.
Причому ймовірність появи події в кожному випробуванні не залежить від
результатів інших випробувань. Такі
випробування називаються незалежними
відносно події
в кожному випробуванні не залежить від
результатів інших випробувань. Такі
випробування називаються незалежними
відносно події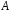 .
Нехай проведено
.
Нехай проведено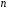 незалежних випробувань. Випадкова
величина
незалежних випробувань. Випадкова
величина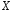 – число появ події
– число появ події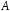 (появу події називають «успіхом») в цій
серії випробувань. Можливими значеннями
цієї випадкової величини є цілі числа
від 0 до
(появу події називають «успіхом») в цій
серії випробувань. Можливими значеннями
цієї випадкової величини є цілі числа
від 0 до .
Ймовірності цих можливих значень
визначаються за формулою Бернуллі.
Закон розподілу такої випадкової
величини називається біноміальним.
.
Ймовірності цих можливих значень
визначаються за формулою Бернуллі.
Закон розподілу такої випадкової
величини називається біноміальним.
Означення.
Дискретна
випадкова величина
 називається розподіленою за біноміальним
законом, якщо її можливими значеннями
називається розподіленою за біноміальним
законом, якщо її можливими значеннями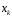 є числа успіхів
є числа успіхів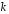 в схемі Бернуллі при
в схемі Бернуллі при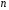 випробуваннях, а ймовірності знаходяться
за формулою Бернуллі
випробуваннях, а ймовірності знаходяться
за формулою Бернуллі
 ,
,
( ,
,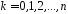 ).
).
Закон розподілу:
|
|
0 |
1 |
... |
|
... |
|
|
|
|
|
|
... |
|
... |
|
|
Звернемо
увагу на те, що сума ймовірностей
 – це точно біном Ньютона
– це точно біном Ньютона
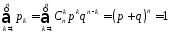 .
.
Цей
факт і вплинув на назву випадкової
величини, яка розглядається. Позначається
біноміальний розподіл так:
 ,
де
,
де і
і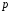 – параметри біноміального розподілу.
– параметри біноміального розподілу.
Функція розподілу:

Числові характеристики:
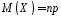 ,
,
 ,
,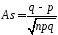 ,
,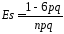 .
.
Найімовірніше
значення
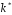 випадкової величини
випадкової величини ,
розподіленої за біноміальним законом
задовольняє нерівність:
,
розподіленої за біноміальним законом
задовольняє нерівність:
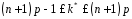 .
.
Приклад.
На заліку студент отримав 4 задачі.
Ймовірність правильно розв’язати кожну
задачу
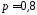 .
Випадкова величина
.
Випадкова величина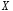 – число правильно розв’язаних задач.
– число правильно розв’язаних задач.
а)
Знайти закон розподілу випадкової
величини
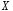 ;
;
б)
побудувати функцію розподілу випадкової
величини
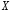 та її графік.
та її графік.
в)
Знайти
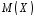 ,
, ,
, .
.
Розв’язання.
а)
Можливі значення випадкової величини
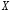 :
0,1,2,3,4. Оскільки можливими значеннями
випадкової величини
:
0,1,2,3,4. Оскільки можливими значеннями
випадкової величини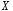 є числа успіхів
є числа успіхів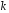 в схемі Бернуллі при 4 випробуваннях,
то їх ймовірності знаходяться за формулою
Бернуллі:
в схемі Бернуллі при 4 випробуваннях,
то їх ймовірності знаходяться за формулою
Бернуллі:
 ,
,
 ,
,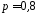 .
.
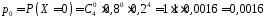 ;
;
 ;
;
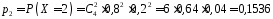 ;
;
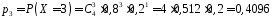 ;
;
 .
.
Закон розподілу запишемо у вигляді таблиці:
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
0,0016 |
0,0256 |
0,1536 |
0,4096 |
0,4096 |
1 |
Перевірка умови нормування:
0,0016+0,0256+0,1536+0,4096+0,4096=1.
Отже,
випадкова величина
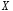 має біноміальний розподіл
має біноміальний розподіл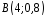 .
.
б)
Функція розподілу випадкової величини
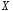 за означенням:
за означенням:

Компактно
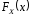 можна записати в такій формі:
можна записати в такій формі:
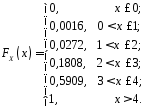
Графік
функції
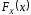 зображено на малюнку:
зображено на малюнку:

в)
Знайдемо
 ,
,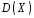 ,
,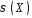 .
.
 ;
;
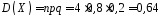 ;
;
 .
.
1.1. Розподіл Бернуллі
Біноміальний
розподіл
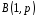 з параметрами
з параметрами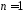 і
і називаєтьсярозподілом
Бернуллі.
називаєтьсярозподілом
Бернуллі.
Числові характеристики:
 ,
,
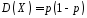 .
.
Розподіл
Бернуллі
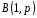 відіграє фундаментальну роль в теорії
ймовірностей і математичний статистиці,
являючись математичною моделлю
випробування з двома наслідками.
відіграє фундаментальну роль в теорії
ймовірностей і математичний статистиці,
являючись математичною моделлю
випробування з двома наслідками.
Якщо
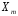 ,
, – незалежні випадкові величини з
розподілом Бернуллі, тоді випадкова
величина
– незалежні випадкові величини з
розподілом Бернуллі, тоді випадкова
величина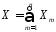 має біноміальний розподіл
має біноміальний розподіл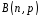 .
.
Приклад.
Нехай в партії деяких виробів якісні
вироби зустрічаються з ймовірністю
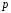 ,
а вироби з дефектом – з ймовірністю
,
а вироби з дефектом – з ймовірністю . Покладемо
. Покладемо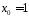 ,
якщо вибрали виріб якісний, і
,
якщо вибрали виріб якісний, і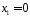 ,
якщо виріб з дефектом. Тоді «якість»
виробів можна описати випадковою
величиною, що має розподіл Бернуллі
,
якщо виріб з дефектом. Тоді «якість»
виробів можна описати випадковою
величиною, що має розподіл Бернуллі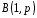 .
.