7. Потужність множин і зліченність

Розглянемо множину натуральних чисел та її скінченну підмножину– відрізок натурального ряду.

Означення. Непорожня множина називаєтьсяскінченною, якщо вона бієктивна деякій підмножині ,. Якщо, то потужність множинидорівнює.

Означення. Непорожня множина називаєтьсязліченною, якщо вона бієктивна множині натуральних чисел .Для позначення потужності зліченної множини використовується символ (алеф-0).

Можна сказати, що множина зліченна, якщо її елементи можна перенумерувати натуральними числами.

Означення. Множини називаються рівнопотужними, якщо між ними можна встановити бієкцію.

Ясно, що рівнопотужні скінченні множини мають однакову потужність – кількість елементів.

Існують нескінченні множини, елементи яких не можна перенумерувати. Такі множини називають незліченними.

Має місце

Теорема Кантора. Множина всіх точок відрізка незліченна.

Означення. Множина, бієктивна множині всіх точок відрізк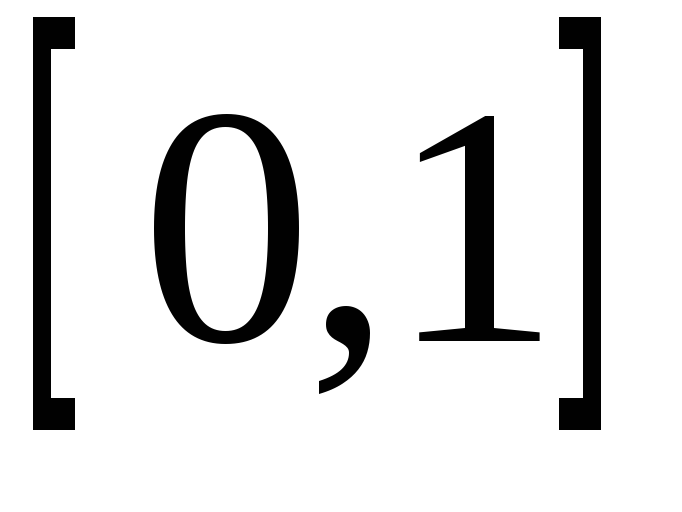а , називаєтьсямножиною потужності континуума.

Оскільки множини точок інтервалів, відрізків і всієї числової прямої рінопотужні, то всі вони мають потужність континуума.

Лекція розроблена доцентом кафедри ВМ,

к.т.н. Скубаком О.М.