5. Поняття функції та відображення

Поняття функції або відображення є одним з центральних в математиці. В математичному аналізі прийнято наступне означення функції. Нехай задано множини і . Змінна називається функцією від змінної , якщо за деяким правилом кожному значенню відповідає одне значення .

Існує інше означення функції як окремого випадку відношення між множинами.

Означення. Функцією називається бінарне відношення між множиною і множиною таке, що для кожного елемента існує один і тільки один елемент , відповідний елементу . Цей елемент називаєтьсязначенням функції для елемента і позначається . Інакше кажучи, функцією називається бінарне відношення, яке не містить двох пар з однаковими першими компонентами і різними другими.

Приклад. 1) – функція;

2) – відношення, але не функція.

Як і для звичайного відношення, для функціонального відношення множина називається множиною відправлення, множина – множиною прибуття. Множина пар називається графіком функції .

Множина називається областю визначення функції ; множина називається областю значень функції .

Приклад. Для попереднього прикладу 1) ,.

Таким чином, символ використовується при означенні функції у двох розуміннях:

• 1) – множина, елементами якої є пари, між якими існує функціональне відношення;

• 2) – позначення для елемента 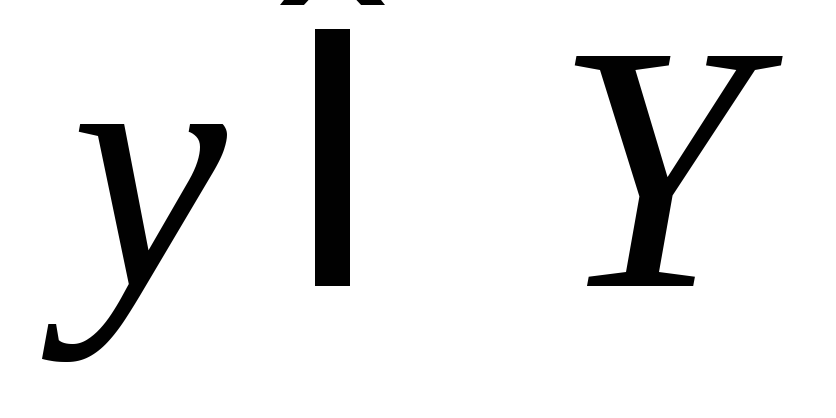, що відповідає даному елементу .

Для функцій застосовується геометрична термінологія. Функцію називають відображенням множини в множину , елемент називається образом при відображенні . Якщо , то будь-який , для якого , називається прообразом елемента . Сукупність всіх прообразів елемента називається повним прообразом елемента і позначається : . Аналогічно визначаються образ множини іпрообраз множини :

;

Означення. Відображення наназиваєтьсяперетворенням множини .

Оскільки функції є бінарними відношеннями, то можна знаходити обернені функції і застосовувати операцію композиції.

Означення. Якщо відношення, обернене до функції , є функціональним, то воно називаєтьсяфункцією, оберненою до і позначається .

Оскільки в оберненому відношенні образи і прообрази міняються місцями, то обернена функція може не існувати.

Приклад: Функція відображає відрізокна відрізок. На відрізкудля неї існує обернена функція.

Означення. Нехай задані функції і. Функціяназиваєтьсякомпозицією функцій і, якщо має місце рівність . Часто кажуть, що функціяотримана підстановкоюв.

В математичному аналізі означення композиції двох функціональних відношень відповідає означенню складеної функції ..

Означення. Вираз, що описує композицію функцій і містить функціональні знаки і символи аргументів, називається формулою.

6. Класифікація функцій

Класифікація функцій
за характером	за виглядом множин і
сюр’єкція (або відображення на ), якщо	–дискретна функція (послідовність)
ін’єкція (або відображення в ), якщо	і –дійсна функцією одного дійсного аргументу; і –дійсна функцією двох дійсних аргументів
бієкція, (взаємнооднозначне відображення), якщо	–сім’я функцій, а , –функціонал. і –сім’ї функцій – оператор.
відображення загального виду, якщо і