Державний університет телекомунікацій

Навчально-науковий інститут Захисту інформації

Кафедра вищої математики

ЗАТВЕРДЖУЮ Завідувач кафедри ВМ ___________________________Барабаш О.В. "___" _____________20___ року

ЛЕКЦІЯ № 2

з навчальної дисципліни

Дискретна математика

Тема № 1. Основні поняття теорії множин.

Заняття № 3. Відношення. Функції.

Навчальний час – 2 години

Для студентів денної форми навчання освітньо-кваліфікаційного рівня бакалавр напряму підготовки

6.050102 – Комп’ютерна інженерія

Навчальна та виховна мета:

1. Сформувати базові знання з основ теорії відношень;

2. Формувати здатність учитися, здатність до системного мислення.

Лекція розроблена доцентом кафедри ВМ,

к.т.н. Скубаком О.М.

Обговорено та схвалено на засіданні кафедри ВМ 31.08.2013 року Протокол № 1

Київ – 2014

Зміст

Вступ.

1. Поняття відношення. Способи задання відношень.

2. Образи і прообрази елементів і множин відносно відношень.

Операції над відношеннями.

3. Властивості бінарних відношень.

4. Спеціальні бінарні відношення.

5. Поняття функції та відображення.

6. Класифікація функцій.

7. Потужність множин і зліченність.

Заключна частина.

ЛIТЕРАТУРА

1. Бардачов Ю.М. та ін. Дискретна математика. – К.: Вища школа, 2002. – 287с. – с. 81-106.

Завдання на самостійну роботу

1. Опрацювати лекційний матеріал.

2. Опрацювати матеріал за підручником.

3. Підготовитися до практичного заняття 2.

Конспект лекції

1. Поняття відношення. Способи задання відношень

Означення. Для будь-яких двох множин і довільна підмножина називається бінарним відношенням між і (або просто на , якщо =).Для впорядкованої пари використовують позначенняі кажуть, щознаходиться у відношенніз.Якщо ж два елементи не зв’язані відношенням, то записуютьабо, або .

Оскільки відношення – це множини, то їх можна задавати переліком елементів або характеристичними властивостями. Крім того, для бінарних відношень існують ще декілька способів їх задання.

Способи задання відношень

1. Перелік елементів. Відношення з прикладу 1

2. За допомогою характеристичної властивості елементів.

3. Матрицею відношення, рядки і стовпці якої відповідають елементам множин і . Пари, які входять у відношення 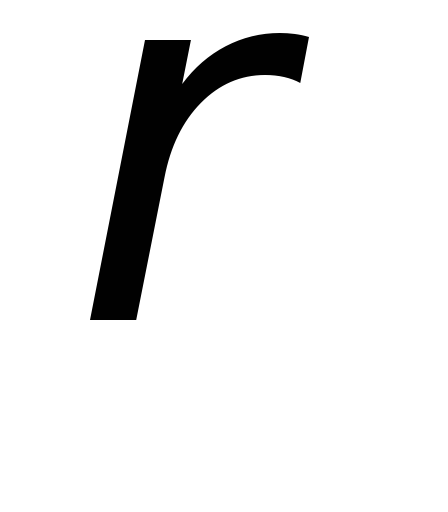, зображуються спеціальним символом, наприклад, 1, на перерізі відповідних рядків і стовпців.

Наприклад, відношення з прикладу 1 може бути задане матрицею:

4. Графіком, який являє собою множину точок на площині з ПДСК, координатами яких є пари з множини .

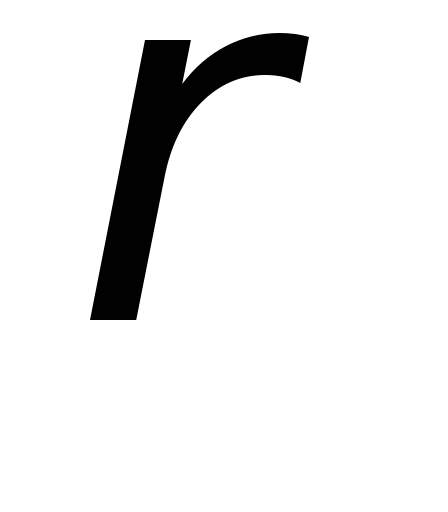Наприклад, графік відношення з прикладу 1 має вигляд:

5. Якщо , то відношення можна задати діаграмою, яка складається з вузлів і стрілок, причому вузлам відповідають елементи множин і , а стрілка з’єднує елемент 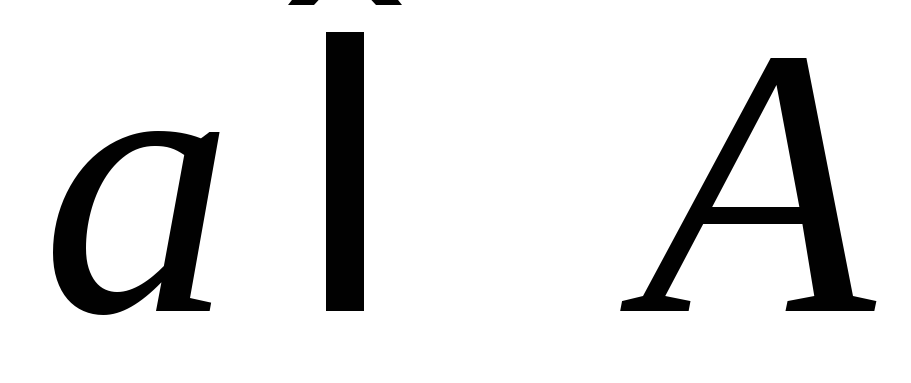з елементом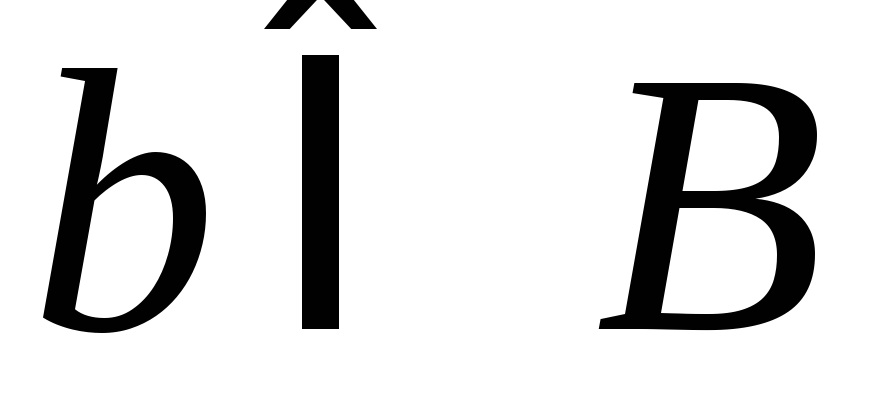тільки у випадку, коли.

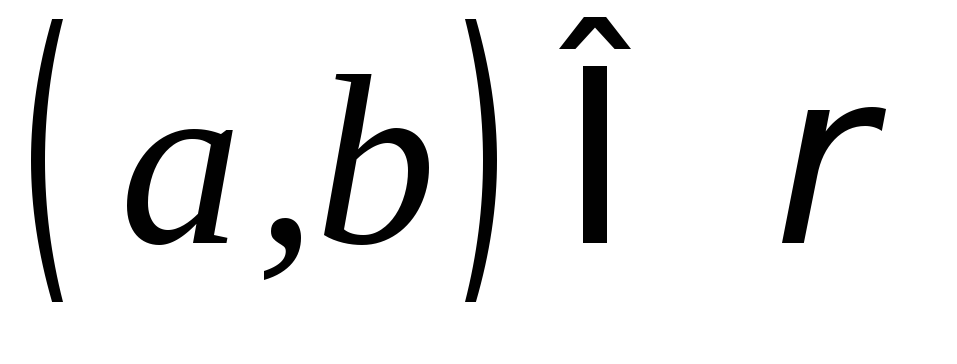Наприклад, відношення з прикладу 1 може бути задане діаграмою

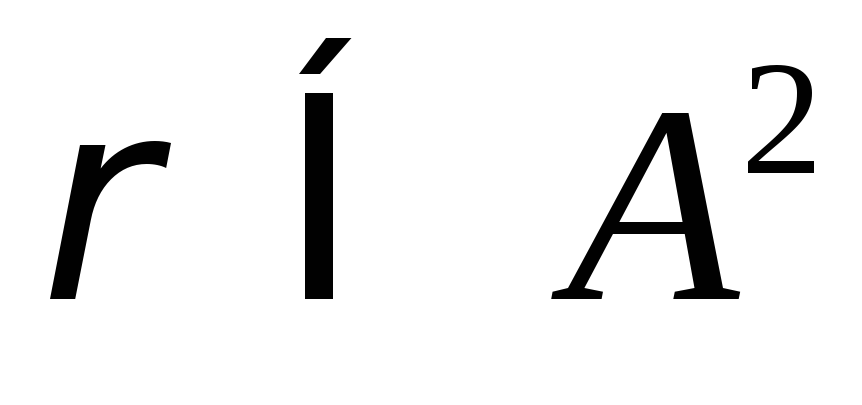6. Якщо , то відношення можна задати графом – сукупністю вузлів, яким відповідають елементи множини , і дуг, напрямлених від до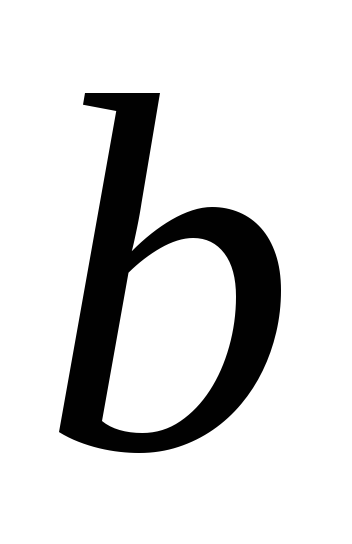тільки у випадку, коли.

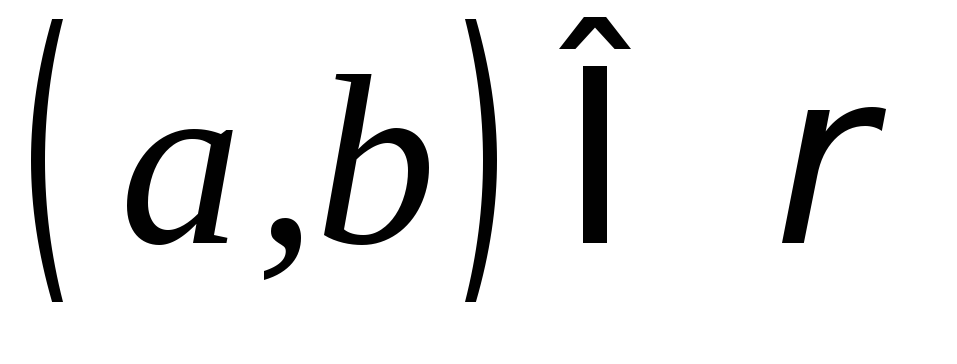Зауваження. Способи задання 4–6 ще називають графічними способами зображення відношень. Графічні способи представлення відношень мають властивість наочності (при невеликих потужностях множин).