
редактированные / 55
.docx
55.Метод векторных диаграмм. Последовательная линейная RLC-цепь синусоидального переменного тока: импеданс, разность фаз, резонансные явления.
Рассмотрим вынужденный колебания по зака
U=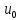 sinwt
sinwt
I=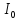 sin(wt+φ)
sin(wt+φ)
t-?
tgφ-?
I=
iR+ -
-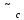 =U
=U
iR+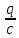 +L
+L
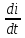 =
=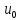 sinwt
sinwt
L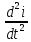 +R
+R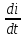 +
+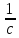 =
=
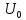 wcoswt
wcoswt
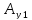 =
=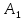 sin(wt+
sin(wt+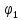 )
)
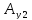 =
=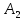 sin(wt+
sin(wt+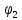 )
)
Метод векторных диаграмм
I=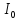 sinwt
(φ=0
для послед.соед.)
sinwt
(φ=0
для послед.соед.)
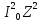 =
=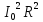 (
(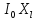 -
-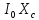 )^2
)^2
Z=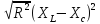 ((все
выражение под корнем))
((все
выражение под корнем))
Tgφ=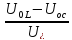 =
=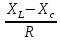
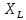 =wL
=wL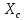 =
=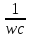
если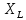 =
=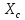 ,то Z
имеет наим. Значение и z=R,
а φ=0
,то Z
имеет наим. Значение и z=R,
а φ=0
wL=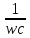 =>
=>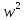 =
=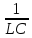 =
=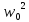
имеет место резонансное явление
 =
=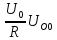 =
=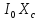
R<<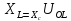 =
=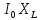
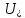 =
=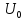
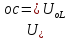 >>
>>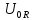 =
=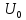
56. Метод комплексных амплитуд. Параллельная линейная RLC-цепь синусоидального переменного тока: импеданс, разность фаз, резонансные явления.
J=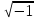
Метод комплексных амплитуд
Формулы
перехода: A=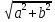 ,
tg
,
tg =
=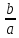
a=Acos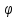
b=Asinϕ
L:R=R(активное сопротивление)
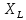 =j
=j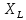
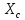 =-j
=-j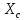
S(полная мощность)
S=U●I*
I*-комплексное число,сопряженное с I(сопряженное-меняется знак Im части или аргумента)
S=P+jQ
Если Q>0- нируктивныйхар-р цепь имеет
Q<0– емкостной
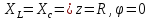
R>>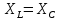
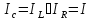
Получается резонанс токов
57. Электромагнитная индукция в трактовке Максвелла: физическое обоснование, интегральная и дифференциальная формы закона электромагнитной индукции Максвелла. Токи Фуко: механизмы возникновения, применение в технике; биологическое действие электромагнитных полей.
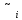 =-
=-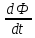
Согласно фарадею явл. электр. Инд. Явл. в том,если есть замкнутый пров. Контур в мам ч\з поверхн. которого возникает ток.
Ɛ=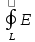 dl
dl
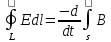 dS
dS
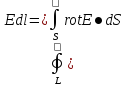
rote=
-
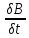
согласно Максвелла: явл. электр. нид. закл: возник. вихрев. электр. поля .
Токи Фуко:
j=jE-закон ома в дифф-лй форме
если поле будет создано в проводящей среде ,то возникнут вихревые токи(токи Фуко).
58. Гипотеза Максвелла о токах смещения: физическое обоснование, теорема о циркуляции напряженности магнитного поля по Максвеллу.
Теорема циркуляции:
Rot H=j
div(rotH)=divj
div(rotH)≡0
div j=0
Уравнение непрерывности:
Div
j+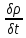 =0
=0
div D=ρ
div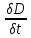 =
=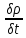
divj+div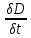 =0
=0
div(j+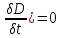
rot
H=j+
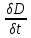
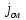 (плотность
тока смещения)
(плотность
тока смещения)
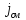 =
=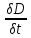
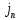 (полного
тока)
(полного
тока)
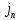 =j+
=j+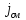 (линии
полного тока всегда замкнуты).
(линии
полного тока всегда замкнуты).
Гипотеза по расширенной трактовке закона электростатической индукции, о взаимном превращение электрических и магнитных полей.
Rot
E=
-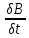
59. Система уравнений Максвелла: интегральная и дифференциальная формы полевых уравнений, материальные уравнения; физический смысл уравнений, их значение в электродинамике.
1.Электр.теор
Гауса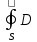 dS=
dS=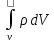
1.Физический смысл divD=ρ
2.Теорема
Гауса для магн поля
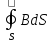
2.Физический смысл divB=0
3.Закон
электромагнитной индукции в трактовке
Фарадея
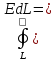 -
-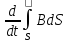
3.В
дифф форме rotE=
-
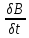
4.Теорема
о циркуляции вектора H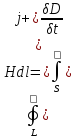 )dS
)dS
4.В
дифф форме rotH=
j+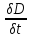
D=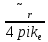 E
; B=4pi
E
; B=4pi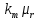 H
H
Закон Ома в дифф форме j=jE
j-удельгая теплопроводность
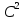 =
=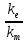 =
9●1
=
9●1
60. Закон сохранения энергии электромагнитного поля: уравнение непрерывности для электромагнитного поля, вектор Умова-Пойнтинга; перемещение энергии электромагнитного поля в пространстве.
Пусть u-обьемная плотность электр полей в этой среде.
u=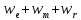
u
=
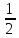 ED+
ED+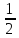 BH +
BH +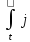 Edt
Edt
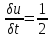 (
(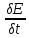 D+E
D+E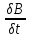 )+
)+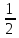 (
( H + B
H + B
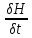 )+jE
)+jE
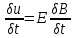 +
H
+
H
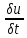 + jE=E (j+
+ jE=E (j+
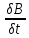 )+H
)+H
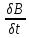
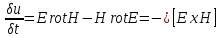
Div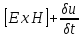 =0
=0
S=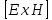
divS
+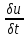 =0
=0
divS
= -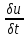
div- расходимость вектора
61. Волновое движение: физическая сущность и волновое уравнение; анализ уравнений Максвелла на соответствие волновому уравнению.
Волновое движение- процесс распределения в пространстве каких либо колебаний.
Волна – физ процесс
S=f(t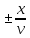 )
)
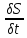 =
=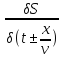 1
1
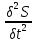 =
=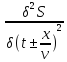 1
1
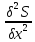 =
=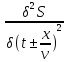 ●
●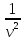
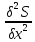 =
=
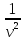 ●
●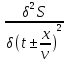
∆S=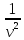 ●
●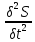 --- волновое уравнение
--- волновое уравнение
62. Плоские электромагнитные волны: физическое обоснование процесса; скорость распространения в линейных диэлектриках; энергия, переносимая электромагнитной волной. Опыты Герца, беспроводный телеграф Попова.
Рассмотрим некоторое электр поле
Волны которые порождают
Т.к. HиE колеблются в одной плоскости то такие электромагнитные волны наз плоскими.
Герц доказал эксперементально что электромагнитные поля сущ.
Закрытый
колебательный контур T=
2Pi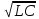
Вибратор Герца:каждая вспышка сопровождалась вспышкой 3 ,так Герц продемонстрировал сущ и распространерие электромагнитных волн.
Беспроводной телеграф -попов
