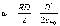редактированные / 9-15
.docx
9. Градиент скалярной функции. Связь между напряженностью электростатического поля и его потенциалом: математическая запись и физический смысл для однородного и неоднородного полей; применение для расчета полей. Уравнение Пуассона
Градиент температуры:
Определение градиента:
Вычисление в декартовых координатах :
Напряженность поля и потенциал
Однородное электрическое поле
Неоднородное электрическое поле
;
=
Физический смысл:
Напряженность электростатического поля направлена так же, как и максимальная скорость убывания потенциала, а по модулю равна модулю этой максимальной скорости
Графическая интерпретация:
Силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям
Уравнение Пуассона div ; =
; - Уравнение Пуассона
10. Проводники и диэлектрики. Электростатическая индукция в проводниках: физическая сущность явления; равновесное распределение напряженности электростатического поля и плотности электрических зарядов в объеме и на поверхности проводников.
Проводники –вещества, которые содержат свободные заряженные частицы. Эти частицы могут перемещаться в пределах всего проводящего тела .
Диэлектрики –вещества, которые содержат заряженные частицы в составе атомов и молекул. Эти частицы могут смещаться в пределах, сравнимых с размерами атомов и молекул
Электростатическое поле внутри проводника
Внутри проводника:
из условия равновесия заряженных частиц: на основании теоремы Гаусса: из соотношения: Электростатический генератор Ван де Граафа , 1931. Принцип действия – полный перенос электрического заряда с внутренней поверхности проводящей сферы на внешнюю
Электростатическое поле вблизи поверхности проводника .Вблизи поверхности проводника силовые линии перпендикулярны эквипотенциальным поверхностям. Применяем теорему Гаусса:
Распределение электрического заряда по поверхности проводника
Потенциал проводящего заряженного шара:
Внутри проводника ,.
Потенциал проводящего шара не зависит от того, как распределен заряд в нем, поскольку весь заряд находится на поверхности шара на одинаковом расстоянии от центра
Потенциалы двух соединенных шаров равны:
Поверхностная плотность электрического заряда и напряженность поля вблизи поверхности проводника обратно пропорциональны радиусу кривизны поверхности в данной точке.
Давление электростатических сил на поверхность проводника
Внутри проводника: .Вблизи поверхности проводника:
На элемент dS действует сила: .
11. Электрическая емкость: емкостные коэффициенты; электрическая емкость конденсатора и уединенного проводника; расчет электрической емкости на примерах плоского конденсатора и уединенного проводящего шара. Системы конденсаторов.
Емкостные коэффициенты
Система жестких, неподвижных проводящих заряженных тел:
Заряды тел и их потенциалы: ,.
Емкостные коэффициенты: .
Электрическая емкость электрического конденсатора
Конденсатор – система двух жестких, неподвижных проводящих тел, которые называются обкладками
Электрическая емкость плоского конденсатора
Размеры обкладок значительно больше расстояния между ними:
Между обкладками плоского конденсатора – поле однородное, а по обе стороны от них – отсутствует: ,
Последовательное соединение конденсаторов
Схема последовательного соединения:
, ,
Паралельное соединение конденсаторов
,
,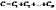
12. Поляризация диэлектриков: физическая сущность явления; поляризационные (связанные) заряды; поляризованность (вектор поляризации); связь вектора поляризации с поверхностной и объемной плотностью связанных зарядов.
Определение:
Поляризация диэлектрика – это явление, которое заключается в появлении связанных электрических зарядов в объеме и на поверхности диэлектрика под действием внешнего электростатического поля
-- объемная плотность связанных зарядов
-поверхностная плотность связанных зарядов
Поляризованность (вектор поляризации)
Определение:
Поляризованность – локальная векторная характеристика степени поляризации диэлектрика
Модуль поляризованности равен дипольному моменту единицы объема диэлектрика
Связь между поляризованностью и плотностью связанных зарядов
Поверхностные связанные заряды:
,
Связь между поляризованностью и плотностью связанных зарядов
Объемные связанные заряды:
.По теореме Остроградского
13. Вектор электрического смещения. Электростатическая теорема Гаусса для вектора электрического смещения: интегральная и дифференциальная формы; применение для расчета электрических полей в диэлектриках; диэлектрическая восприимчивость и относительная диэлектрическая проницаемость вещества.
Напряженность электрического поля в диэлектрике явл суперпозицией напряженности электрического поля сторонних зарядов электрического поля связанных зарядов :
.
В
неоднородной диэлектрической среде  имеет
различные значения, изменяясь на границах
диэлектриков скачкообразно (претерпевая
разрыв). Это затрудняет применение
формул, описывающих взаимодействие
зарядов в вакууме. Что касается теоремы
Гаусса, то в этих условиях она вообще
теряет смысл. В самом деле, благодаря
различной поляризуемости разнородных
диэлектриков напряженности поля в них
будут различными. Поэтому различно и
число силовых линий в каждом диэлектрике
(рис.14.6).
имеет
различные значения, изменяясь на границах
диэлектриков скачкообразно (претерпевая
разрыв). Это затрудняет применение
формул, описывающих взаимодействие
зарядов в вакууме. Что касается теоремы
Гаусса, то в этих условиях она вообще
теряет смысл. В самом деле, благодаря
различной поляризуемости разнородных
диэлектриков напряженности поля в них
будут различными. Поэтому различно и
число силовых линий в каждом диэлектрике
(рис.14.6).
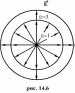
Часть
линий, исходящих из зарядов, окруженных
замкнутой поверхностью, будет заканчиваться
на границе раздела диэлектриков и не
пронижет данную поверхность. Это
затруднение можно устранить, введя в
рассмотрение новую физическую
характеристику поля – вектор электрического
смещения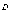
|
|
(14.8) |
Вектор 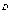 направлен
в ту же сторону, что и
направлен
в ту же сторону, что и 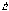 .
В отличие от напряженности
поля
.
В отличие от напряженности
поля 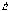 вектор
вектор 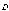 имеет
постоянное значение во всех диэлектриках.
Поэтому электрическое поле в неоднородной
диэлектрической среде удобнее
характеризовать не напряженностью
имеет
постоянное значение во всех диэлектриках.
Поэтому электрическое поле в неоднородной
диэлектрической среде удобнее
характеризовать не напряженностью 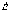 ,
а смещением
,
а смещением 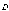 .
С этой целью вводится понятие линий
вектора
.
С этой целью вводится понятие линий
вектора 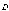 и
потока смещения, аналогично понятию
силовых линий и потока напряженности
и
потока смещения, аналогично понятию
силовых линий и потока напряженности
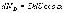
или
|
|
(14.9) |
Используя теорему Гаусса
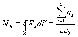
домножим
обе части на 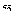
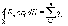
С учетом (14.8) получаем
|
|
(14.10) |
Это уравнение выражает теорему Гаусса для вектора электрического смещения: полный поток вектора электрического смещения через произвольную замкнутую поверхность равен сумме свободных зарядов, заключенных в этой поверхности.
Для векторного
поля 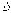 справедлива
интегральная форма теоремы Гаусса:
справедлива
интегральная форма теоремы Гаусса:
|
и, соответственно, дифференциальная форма теоремы Гаусса:
где
|
Величина, характеризующая способность диэлектриков к поляризации. Количественно Д. в. — коэффициент пропорциональности χ в соотношении P = χЕ, где Е — напряжённость электрического поля, P — поляризация диэлектрика (дипольный момент единицы объёма диэлектрика). Д. в. характеризует диэлектрические свойства вещества так же, как и Диэлектрическая проницаемость ε, с которой она связана соотношением: ε = 1 + 4πχ.
14. Потенциальная энергия взаимодействия электрических зарядов: система точечных зарядов; система заряженных проводников; энергия заряженного конденсатора.
По принципу суперпозиции полей потенциал системы точечных зарядов равен алгебраической сумме потенциалов полей, создаваемых в данной точке каждым зарядом в отдельности. Это очевидно, так как:
Е = Е1 + Е2 = – grad1 – grad2 = – grad (1 + 2).
Следовательно, потенциал 0 поля, создаваемого системой точечных зарядов qi, равен
0(r)
= 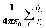 , (7.3)
, (7.3)
где ri – длина радиус-вектора, проведенного от i-го заряда к точке поля с координатами r{x,y,z}.
Потенциал поля проводящей сферы.
Поскольку
напряженность электрического поля
проводящей сферы определяется (вне
сферы) таким же выражением, что и
напряженность поля точечного заряда,
то зависимость потенциала от расстояния
r от центра сферы до данной точки будет
равна: (r)
= 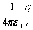 .
Так как электрическое поле внутри
проводящей сферы равно нулю, то при
r R
потенциал постоянен и равен потенциалу
поверхности сферы:
.
Так как электрическое поле внутри
проводящей сферы равно нулю, то при
r R
потенциал постоянен и равен потенциалу
поверхности сферы:
(r R)
= 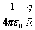 ,
где R – радиус сферы.
,
где R – радиус сферы.
Энергия заряженного конденсатора
Если на обкладках конденсатора электроемкостью С находятся электрические заряды +q и -q, то согласно формуле (20.1) напряжение между обкладками конденсатора равно

В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0.
Среднее значение напряжения в процессе разрядки равно

Для работы А, совершаемой электрическим полем при разрядке конденсатора, будем иметь:
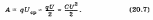
Следовательно, потенциальная энергия Wp конденсатора электроемкостью С, заряженного до напряжения U, равна
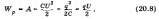
Энергия конденсатора обусловлена тем, что электрическое поле между его обкладками обладает энергией. Напряженность Е поля пропорциональна напряжению U, поэтому энергия электрического поля пропорциональна квадрату его напряженности.
15. Объемная плотность энергии электрического поля. Механические силы в электростатическом поле: метод виртуальных перемещений; давление электростатических сил.
Это
физическая величина, численно равная
отношению потенциальной энергии поля,
заключенной в элементе объема, к этому
объему. Для однородного поля объемная
плотность энергии равна 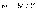 .
Для плоского конденсатора, объем которого
Sd, где S - площадь пластин, d - расстояние
между пластинами, имеем
.
Для плоского конденсатора, объем которого
Sd, где S - площадь пластин, d - расстояние
между пластинами, имеем
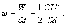
С
учетом, что 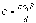 и
и 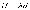
|
|
(16.4) |
или
|
|
(16.5) |
На границе двух диэлектриков с различными диэлектрическими проницаемостями , и при наличии внешнего поля возникают поляризационные заряды разного знака с различными поверхностными плотностями зарядов и (рис.14.7).
Дополнительное поле, создаваемое этими зарядами, перпендикулярно поверхности, поэтому нормальные составляющие полей , и в обеих средах у границы раздела различны, а касательный составляющие одинаковы, т.е.
(14.11)
Векторы электростатического смещения в обеих средах соответственно равны
и (14.12)
Аналогично рассмотренному выше случаю границы диэлектрик - вакуум нормальная составляющая вектора на границе двух диэлектриков а отсюда следует, что
Из этого выражения следует, что в случае и линии вектора при переходе через границу раздела преломляются, отклоняясь от перпендикуляра к границе раздела. Из (14.11) и (14.12) следует, что
При и
При переходе через границу раздела из диэлектрика с меньшим значением в диэлектрик с большим значением , нормальная составляющая вектора остается неизменной, а касательная увеличивается, так что линии вектора преломляются под таким же углом как и линии напряженности поля (рис. 14.8).
Таким образом, при переходе через границу раздела двух диэлектриков изменяется не только вектор напряженности электрического поля , но и вектор . Однако поток вектора через произвольную площадку на границе раздела, равный по определению , с обеих сторон поверхности на основании остается неизменным. Следовательно, число линий вектора электрического смещения, переходящих через границу, не меняется. Поэтому теорема Гаусса остается справедливой для вектора в самом общем случае при наличии в поле диэлектриков любой формы и размеров.

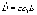
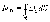
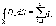
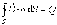
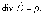
 -
объемная плотность свободных зарядов.
-
объемная плотность свободных зарядов.