Вопросы к экзамену по дисциплине Высшая математика

1 Курс, для студентов специальности информационные системы и технологии в экономике дневной формы обучения

1. Комплексные числа. Алгебраическая, тригонометрическая, показательная форма записи комплексного числа. Действия над комплексными числами в разных формах.

2. Извлечение корня n-ой степени из комплексного числа (вывод формулы). Извлечение квадратного корня из комплексного числа .

3. Матрицы. Виды матриц. Операции над матрицами, их свойства. Транспонирование матриц. Доказательство свойств операции транспонирования. Элементарные преобразования матриц. Эквивалентные матрицы.

4. Определители квадратных матриц. Свойства определителей и методы нахождения. Теорема Лапласа и теорема аннулирования.

Теорема лапласа.

Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Алгебраическим дополнением элемента определителя  называется его минор , взятый со знаком 

Девятое свойство определителя носит название теорема аннулирования:

сумма всех произведений элементов одной строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю

1. Обратная матрица. Доказательство единственности и свойств.

Обратной матрицей для квадратной матрицы А порядка n называется матрица , если выполняются равенства

,                                      (1)

где Е – единичная матрица порядка n.

Доказательство единственности

А имеет единственную обратную матрицу . Докажем это утверждение.

Пусть для матрицы А существует две обратные матрицы ,, то есть

 и .

Тогда =ּ=ּ() =

= (ּ) ===.

Что и требовалось доказать.

5. Вывод формулы для нахождения . Нахождение с помощью элементарных преобразований. Решение матричных уравнений с помощью .

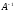6. Системы ЛАУ. Общие понятия. Системы с невырожденной квадратной матрицей и методы их решения (метод обратной матрицы, метод Крамера с выводом формул).

7. Метод Гаусса решения систем ЛАУ (прямой и обратный ход). Решение матричных уравнений с помощью элементарных преобразований.

8. Модель Леонтьева межотраслевого баланса. Продуктивность.

9. Векторы. Основные определения. Линейные операции над векторами. Доказательство необходимого и достаточного условия коллинеарности двух ненулевых векторов.

Необходимое и достаточное условие коллинеарности двух векторов.

Напомним определение коллинеарных векторов, которое было дано в статье векторы – основные определения.

Определение.

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.

Это определение позволяет установить коллинеарность векторов по их изображению на плоскости с некоторой степенью точности, которая зависит от качества чертежа. Поэтому, мы нуждаемся в алгебраическом (а не в геометрическом) условии, выполнение которого будет указывать на коллинеарность двух векторов. Получим его.

Так как операция умножения вектора на число соответствует сжатию или растяжению вектора при неизменном или противоположном направлении, то вектор , где  - произвольное действительное число, коллинеарен вектору . Справедливо и обратное утверждение: если вектор  коллинеарен ненулевому вектору , то он может быть представлен в виде .

Таким образом, мы пришли к необходимому и достаточному условию коллинеарности двух ненулевых векторов: для коллинеарности двух векторов  и  необходимо и достаточно, чтобы они были связаны равенствами  или .

Перейдем к координатной форме полученного условия коллинеарности двух векторов.

Пусть вектор  задан в прямоугольной декартовой системе координат на плоскости и имеет координаты , тогда вектор  имеет координаты  (при необходимости смотрите статью операции над векторами в координатах). Аналогично, если вектор  задан в прямоугольной системе координат трехмерного пространства как , то вектор  имеет координаты .

Следовательно, для коллинеарности двух ненулевых векторов  и  на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями:  или .

Для коллинеарности двух ненулевых векторов  и  в пространстве необходимо и достаточно, чтобы  или .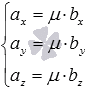

Получим еще одно условие коллинеарности двух векторов, основанное на понятии векторного произведения векторов  и .

Если ненулевые векторы  и  коллинеарны, то по определению векторного произведения , что равносильно равенству . А последнее равенство возможно лишь тогда, когда векторы  и  связаны соотношениями  или , где  - произвольное действительное число (это следует из теоремы о ранге матрицы), что указывает на коллинеарность векторов  и . Таким образом, два ненулевых вектора  и  коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Перейдем к применению условий коллинеарности векторов при решении примеров.

Пример.

Коллинеарны ли векторы  и .

Решение.

Проверим выполнение необходимого и достаточного условия коллинеарности двух векторов на плоскости в координатах :

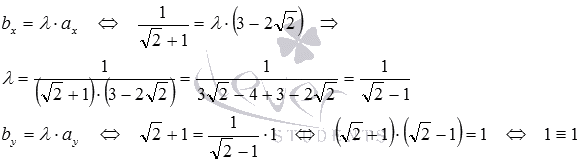
Таким образом, , следовательно, векторы коллинеарны.

Ответ:

векторы  и  коллинеарные.

10. Алгебраическое описание вектора. Направляющие косинусы.

Вектор – это направленный отрезок прямой.

Направляющие косинусы вектора a

 – это косинусы углов, которые вектор образует с положительными полуосями координат.

Свойство: Сумма квадратов направляющих косинусов равна единице.

.

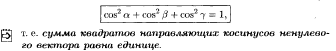
11. Проекция вектора на ось. Свойства проекций с доказательством.

12. Скалярное произведение векторов. Вывод формулы скалярного произведения через координаты. Свойства скалярного произведения. Доказательство необходимого и достаточного условия ортогональности двух ненулевых векторов.

Условие ортогональности двух векторов:

 или .

Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.

13. Векторное произведение векторов. Доказательство свойств, применение.

14. Смешанное произведение векторов. Доказательство свойств, применение.

15. Линейное (векторное пространство). Определение и примеры.

 Совокупность n действительных чисел x₁, х₂,..., х_n, заданных в определенном порядке, называется n-мерным вектором.

1) х + у = у + х; 2)(x + y) + z = x + {y + z); 3) х + 0 = 0; 4) х + (-х) = 0; 5) (х) = (х)х; 6) (х + у) = х + у; 7) ( + х) = х + хx; 8) 1 • x = х.

16. Линейная зависимость и независимость системы векторов. Доказательство утверждений о линейной независимости.

Векторы  называются линейно зависимыми, если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.

В противном случае, т.е. когда соотношение  выполняется только при , эти векторы называютсялинейно независимыми.