2. Скалярное произведение векторов в координатной форме

Пусть даны векторы и. Тогда скалярное произведение векторови:

= вычисляется по формуле:

(3.18)

Скалярное произведение векторов равно сумме произведения одноименных координат. Из (3.18) следует, что необходимым и достаточным условием перпендикулярности векторов а и в является равенство:

(3.19)

Из определения скалярного квадрата (3.18) и из формулы (3.19) найдём:(или =(3.20)

Теперь найдём угол между двумя векторами и. На основании определения скалярного произведения имеем:cos

Тогда cos (3.21)

3.Проекция вектора на ось

Пусть дана некоторая ось х, которая составляет с осями координат углы и дан вектор. Найдём проекцию вектора на ось х.

На оси х зададим единичный вектор

Найдём пр-угол между векторамии.

но т.к , то получим (, отсюдаИтак, Хcos+Уcos+Zcos (3.22)

Пример1: Даны три точки А(1;1;1), В(2;2;1) и С(2;1;2). Найти косинус угла

Решение: Найдём векторы . На основании формулы (3.21).

cos

Пример 2: Даны точки А(1;1;1) и В(4;5;3). Найти проекцию вектора АВ на ось х, составляющие с координатными осями равные острые углы.

Решение: Пусть cos, cos, cos- направляющие косинусы оси х и по условию задачи: cos= cos= cos. Зная, что cos+cos+cos=1, имеем cos cos. Вектортогда по формуле (3.22):

4. Векторное произведение векторов

Определение: Векторным произведением двух векторов иназывается вектор, обозначаемый символомиликоторый определяется следующими тремя условиями:

1. Модуль векторного произведения =равен гдеугол между векторамии;

2. Вектор =перпендикулярен к каждому из векторови;

3. Вектор направлен таким образом, чтобы смотря в направлении от конца векторана плоскость вектораикратчайший поворот откбыл виден против хода часовой стрелки.

Из определения векторного произведения вытекают следующие свойства:

1. Если векторы иколлинеарны, то их векторное произведение равно нулю.

2. Модуль векторного произведения двух векторов иравен площади параллелограмма построенного на этих векторах.

3. При перестановке местами сомножителей векторное произведение меняет свой знак:

4. Векторное произведение подчиняется распределительному закону:

5. Векторное произведение подчиняется сочетательному закону по отношению к скалярному множителю: где - число.

5. Векторное произведение в координатной форме

Пусть даны векторы

На основании определения и свойств векторного произведения легко показать, что:

. (3.23)

.

На основании свойства и (6.1) можно установить, что:

или

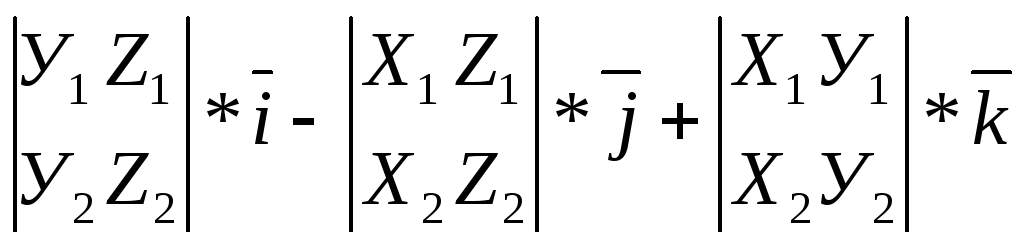=(3.24)

Получим разложение векторного произведения по базисуСледовательно координаты векторного произведения определяются:

=(3.25)

Заметим, что в формуле (3.24) можно придать вид:

=(3.26)

Пример 1: Даны векторы и.Разложить вектор по базису .

Решение: Используем формулу (3.25) и получим:

или

Координаты векторного произведения

Пример 2: Даны три точки А(1;1;1), В(4;3;5). Найти площадь Sтреугольника АВС.

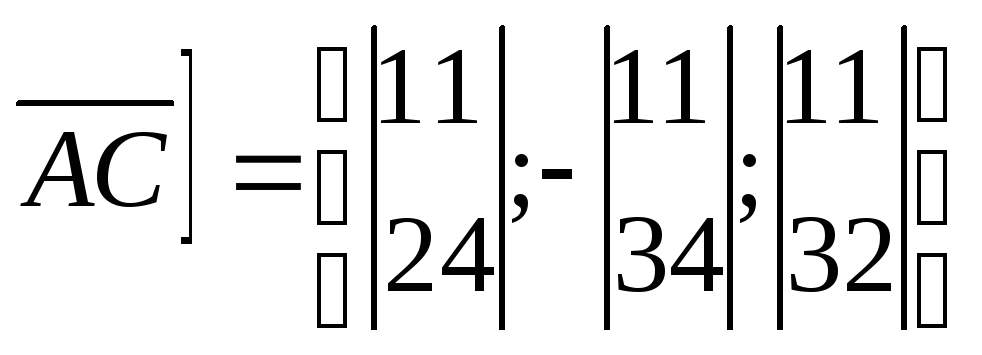Решение: Определим координаты векторов и: . Модуль векторного произведения векторовравен площади параллелограмма, построенного на этих векторах. Площадь треугольника АВС:. По формуле (3.26) найдем координаты.или

Тогда