
1.5 Метод хорд
Пусть уравнение
(1.1) имеет на отрезке
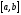 один корень, а функция
один корень, а функция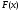 на этом отрезке непрерывна. Пусть для
определенности функция
на этом отрезке непрерывна. Пусть для
определенности функция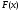 возрастает и выпукла вверх, причем и
возрастает и выпукла вверх, причем и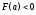 ,
,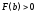 ,
что соответствует рисунку 9.
,
что соответствует рисунку 9.
Геометрический
смысл метода хорд состоит в том, что
дуга кривой
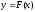 заменяется хордой и ищется точка
пересечения хорды с осью абсцисс, которая
и берется в качестве следующего
приближения к решению.
заменяется хордой и ищется точка
пересечения хорды с осью абсцисс, которая
и берется в качестве следующего
приближения к решению.
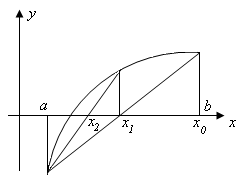
Рис. 9
Из рисунка видно,
что левый конец интервала остается
неподвижным, а правый конец выбран в
качестве начального приближения к
корню:
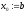 ,
, .
Из уравнения прямой, проведенной через
точки
.
Из уравнения прямой, проведенной через
точки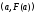 и
и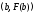 получим значение
получим значение ,
равное абсциссе точки пересечения хорды
с осью абсцисс. Корень теперь находится
на отрезке
,
равное абсциссе точки пересечения хорды
с осью абсцисс. Корень теперь находится
на отрезке .
Применяя снова метод хорд, проведем
прямую через точки
.
Применяя снова метод хорд, проведем
прямую через точки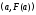 и
и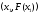 ,
получим
,
получим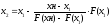 и т.д.
и т.д.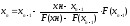 .
Получаем последовательность приближенных
значений
.
Получаем последовательность приближенных
значений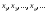 ,
каждый последующий член которой ближе
к истинному значению корня, чем предыдущий.
Рассмотрим случай, когда функция
,
каждый последующий член которой ближе
к истинному значению корня, чем предыдущий.
Рассмотрим случай, когда функция возрастает и выпукла вниз, и
возрастает и выпукла вниз, и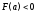 ,
,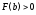 ,
что соответствует рисунку 10.
,
что соответствует рисунку 10.
В данном случае
правый конец интервала остается
неподвижным, а левый конец выбран в
качестве начального приближения к
корню:
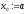 ,
,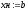 .
Заметим, что за начальное приближение
к корню выбирается тот конец интервала,
где функция и вторая производная имеют
значения разных знаков, а другой конец,
где функция и вторая производная имеют
одинаковые знаки остается неподвижным.
.
Заметим, что за начальное приближение
к корню выбирается тот конец интервала,
где функция и вторая производная имеют
значения разных знаков, а другой конец,
где функция и вторая производная имеют
одинаковые знаки остается неподвижным.
Рассмотрим случай,
когда функция
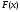 убывает и выпукла вверх, и
убывает и выпукла вверх, и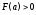 ,
,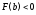 ,
что соответствует рисунку 11. В данном
случае правый конец интервала остается
неподвижным, а левый конец выбран в
качестве начального приближения к
корню:
,
что соответствует рисунку 11. В данном
случае правый конец интервала остается
неподвижным, а левый конец выбран в
качестве начального приближения к
корню: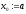 ,
,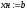 .
.
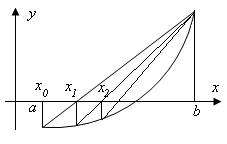
Рис. 10
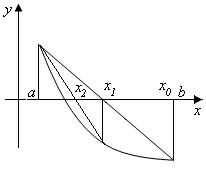
Рис. 12
Возможен случай,
когда функция
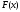 убывает и выпукла вниз, и
убывает и выпукла вниз, и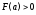 ,
,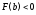 ,
что соответствует рисунку 12. В данном
случае левый конец интервала остается
неподвижным, а правый конец выбран в
качестве начального приближения к
корню:
,
что соответствует рисунку 12. В данном
случае левый конец интервала остается
неподвижным, а правый конец выбран в
качестве начального приближения к
корню: ,
, .
.
Рис. 11
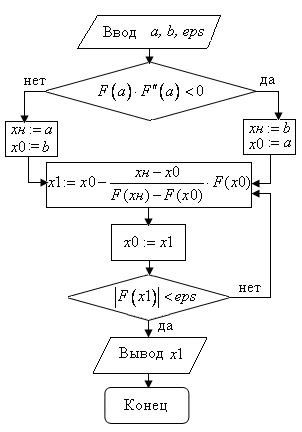
Рис. 13
Итак, если
функция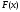 непрерывна, а вторая производная
сохраняет свой знак на отрезке
непрерывна, а вторая производная
сохраняет свой знак на отрезке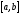 ,
то уравнение
,
то уравнение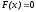 имеет единственный корень, а
последовательность
имеет единственный корень, а
последовательность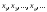 монотонно к нему сходится. В качестве
нулевого приближения к корню выбирается
тот конец интервала, где функция и вторая
производная имеют значения разных
знаков,
монотонно к нему сходится. В качестве
нулевого приближения к корню выбирается
тот конец интервала, где функция и вторая
производная имеют значения разных
знаков,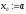 ,
а другой конец, где функция и вторая
производная имеют одинаковые знаки
остается неподвижным.
,
а другой конец, где функция и вторая
производная имеют одинаковые знаки
остается неподвижным.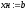 .
.
На рисунке 13
изображена блок -схема алгоритма
уточнения одного корня уравнения (1.1)
на отрезке
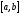 до заданной степени точности
до заданной степени точности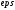 методом хорд.
методом хорд.
1.6 Метод Ньютона (касательных)
Пусть корень
уравнения (1.1) отделен на отрезке
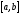 ,
причем
,
причем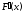 и
и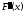 непрерывны и сохраняют знаки на всем
отрезке
непрерывны и сохраняют знаки на всем
отрезке .
Геометрический смысл метода Ньютона
состоит в том, что дуга кривой заменяется
касательной к этой кривой и ищется точка
пересечения касательной с осью абсцисс,
которая и берется в качестве следующего
приближения к решению уравнения (1.1).
.
Геометрический смысл метода Ньютона
состоит в том, что дуга кривой заменяется
касательной к этой кривой и ищется точка
пересечения касательной с осью абсцисс,
которая и берется в качестве следующего
приближения к решению уравнения (1.1).
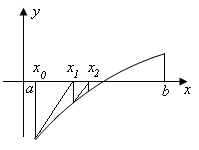
Рис. 14
Предположим, для
определенности, что
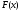 возрастает и выпукла вверх, и
возрастает и выпукла вверх, и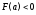 ,
,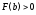 ,
что соответствует рисунку 14.
,
что соответствует рисунку 14.
Интуитивно ясно,
если провести касательную к кривой
 в точке
в точке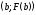 ,
то она пересечет ось абсцисс в точке,
не принадлежащей
,
то она пересечет ось абсцисс в точке,
не принадлежащей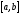 .
Поэтому проведем касательную к кривой
.
Поэтому проведем касательную к кривой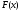 в точке
в точке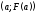 ,
т.е. за начальное приближение к корню
возьмем левый конец интервала
,
т.е. за начальное приближение к корню
возьмем левый конец интервала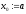 .
Найдем абсциссу точки пересечения
касательной с осью
.
Найдем абсциссу точки пересечения
касательной с осью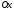 ,
получим
,
получим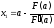 .
Корень теперь находится на отрезке
.
Корень теперь находится на отрезке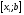 .
Применяя снова метод Ньютона, проведем
касательную в точке
.
Применяя снова метод Ньютона, проведем
касательную в точке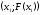 ,
получим
,
получим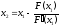 и т.д.
и т.д.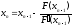 .
Получили последовательность приближенных
значений
.
Получили последовательность приближенных
значений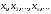 ,
каждый последующий член которой ближе
к истинному значению корня, чем предыдущий.
,
каждый последующий член которой ближе
к истинному значению корня, чем предыдущий.
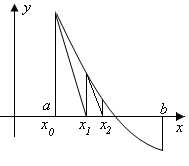
Рис. 15
Рассмотрим случай,
когда функция
 убывает и выпукла вниз, и
убывает и выпукла вниз, и ,
, ,
что соответствует рисунку 15. Ясно, если
провести касательную к кривой
,
что соответствует рисунку 15. Ясно, если
провести касательную к кривой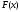 в точке
в точке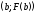 ,
то она пересечет ось абсцисс в точке,
не принадлежащей
,
то она пересечет ось абсцисс в точке,
не принадлежащей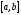 .
Поэтому проведем касательную к кривой
.
Поэтому проведем касательную к кривой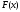 в точке
в точке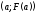 ,
т.е. за начальное приближение к корню
возьмем левый конец интервала
,
т.е. за начальное приближение к корню
возьмем левый конец интервала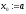 .
.
Предположим, что
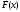 возрастает и выпукла вниз, и
возрастает и выпукла вниз, и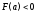 ,
,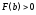 ,
что соответствует рисунку 16. В данном
случае за нулевое приближение к корню
следует выбрать правый конец интервала
,
что соответствует рисунку 16. В данном
случае за нулевое приближение к корню
следует выбрать правый конец интервала ,
т.е.
,
т.е. .
.
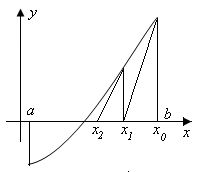
Рис. 16.
Рассмотрим случай,
когда функция
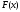 убывает и выпукла вверх, и
убывает и выпукла вверх, и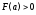 ,
,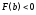 ,
что соответствует рисунку 17. Ясно,
если провести касательную к кривой
,
что соответствует рисунку 17. Ясно,
если провести касательную к кривой в точке
в точке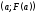 ,
то она пересечет ось абсцисс в точке,
не принадлежащей
,
то она пересечет ось абсцисс в точке,
не принадлежащей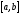 .
Поэтому проведем касательную к кривой
.
Поэтому проведем касательную к кривой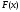 в точке
в точке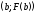 ,
т.е. за начальное приближение к корню
возьмем левый конец интервала
,
т.е. за начальное приближение к корню
возьмем левый конец интервала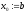 .
.
Итак, существует
общее правило: за исходную точку следует
выбирать тот конец отрезка
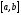 ,
в котором знак функции совпадает со
знаком второй производной. Метод Ньютона
эффективен для решения тех уравнений,
для которых значение модуля производной
,
в котором знак функции совпадает со
знаком второй производной. Метод Ньютона
эффективен для решения тех уравнений,
для которых значение модуля производной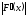 достаточно велико, т.е. график функции
достаточно велико, т.е. график функции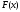 в окрестности корня имеет большую
крутизну. Для условия окончания
итерационного процесса может быть
использовано условие
в окрестности корня имеет большую
крутизну. Для условия окончания
итерационного процесса может быть
использовано условие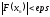 или условие близости двух соседних
приближений:
или условие близости двух соседних
приближений:
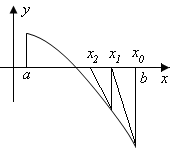
Рис. 17.
 ,
где
,
где
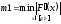 ,
,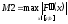 .(см.
[11]).
.(см.
[11]).
На рисунке 18
изображена схема алгоритма уточнения
одного корня уравнения (1.1) на отрезке
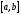 методом Ньютона до заданной степени
точности
методом Ньютона до заданной степени
точности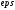 .
.
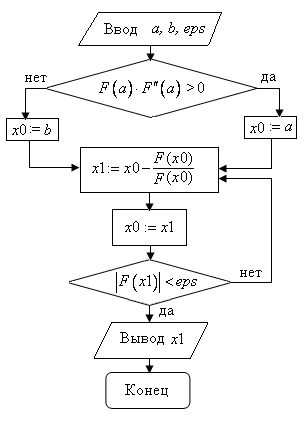
Рис. 18.
При оценке эффективности численных методов существенное значении имеют следующие свойства:
универсальность
простота организации вычислительного процесса
скорость сходимости.
С этой точки зрения,
наиболее универсальным является метод
половинного деления, поскольку он
требует только непрерывности функции
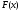 .
.
С точки зрения организации вычислительного процесса все методы очень просты.
Наибольшей скоростью сходимости обладает метод Ньютона.
